 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Помилки вибірки
Спочатку наведемо основні умовні позначення. Чисельність одиниць генеральної сукупності позначимо через N, вибіркової — п. Узагальнюючі характеристики генеральної сукупності - середня, дисперсія, частка — називаються генеральними і відповідно позначаються х, а2, р, де р - відношення числа М одиниць, що мають дану ознаку, до загальної чисельності генеральної сукупності (N), р = M/N.
Узагальнюючі характеристики вибіркової сукупності мають назву вибіркових і відповідно позначаються х 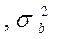 , W, де W=m/n.
, W, де W=m/n.
Теорія обчислення випадкових помилок базується на працях видатних вчених Я. Бернуллі, С. Пуассона, П.Л. Чебишева, А.А. Маркова, A.M. Ляпунова та ін.
Закон великих чисел - загальний принцип, згідно з яким сукупна дія великого числа незалежних факторів призводить до результату, який майже не залежить від випадку. В соціально-економічній статистиці це може бути сформульовано так: кількісні закономірності, які властиві масовим явищам, виразно проявляються лише при достатньо великому числі спостережень.
У кожній окремій вибірці із усіх можливих випадкова помилка вибірки  може приймати різні значення. При великій кількості спостережень розподіл випадкових помилок середньої величини і частки наближається до нормального.
може приймати різні значення. При великій кількості спостережень розподіл випадкових помилок середньої величини і частки наближається до нормального.
Отже, можна вести мову про середню помилку вибірки. Доведено, що при простому випадковому відборі, проведеному за системою повторного відбору:

Якщо вибіркове спостереження застосовується для визначення частки ознаки, то середня помилка частки обчислюється за формулою

Використовуючи функцію нормального розподілу, можна обчислити імовірність граничної помилки певного розміру. Так, імовірність того, що в окремій вибірці помилка не перевищить 2 µ, становить 0,954, а не перевищить 3 µ — 0,997.
У наведених формулах  та pq - характеристики генеральної сукупності, котрі при вибірковому спостереженні невідомі. На практиці їх замінюють вибірковими характеристиками.
та pq - характеристики генеральної сукупності, котрі при вибірковому спостереженні невідомі. На практиці їх замінюють вибірковими характеристиками.
При безповторному відборі середня помилка вибірки дорівнює:

а помилка частки:

Для вирішення практичних завдань обчислення середньої помилки вибірки недостатньо, тому визначають граничний для певної імовірності розмір вибіркової помилки 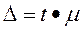 , де t — квантиль нормального розподілу, який називають коефіцієнтом довіри.
, де t — квантиль нормального розподілу, який називають коефіцієнтом довіри.
Розглянемо приклади визначення граничної помилки середньої та частки.
Приклад 4.1
З отари овець загальною чисельністю 1000 голів (N) вибірковій контрольній стрижці було піддано 100 голів (n) середній настриг вовни при цьому становив 4,2 кг на одну вівцю при середньому квадратичному відхиленні 1,5 кг. Визначити межі, в яких знаходиться середній настриг вовни для усіх 1000 голів з імовірністю 0,954 (t = 2).
У даному разі маємо простий випадковий відбір, до того ж, зрозуміло, безповторний. Підставимо дані у відповідні формули:
 кг
кг
 кг
кг
Тоді одне із можливих значень, в межах яких може знаходитись середній настриг вовни, розраховуєтся за формулою

У загальному вигляді це записується таким чином:
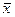 = 4,2 ± 0,284,
= 4,2 ± 0,284,
що дорівнює:
3,92  х
х  4,48.
4,48.
Таким чином, на підставі проведеної вибірки гарантуємо, що у 954 випадках із 1000 середній настриг вовни буде знаходитися в межах: від 3,9 до 4,4 кг на одну вівцю.
Приклод 4.2
Для визначення якості продукції відібрано 500 одиниць з 10 000. Серед них виявлено 50 виробів третього сорту. Визначити граничну помилку частки з імовірністю 0,997.
Маємо, що частка виробів третього сорту становить
W = 50/500 = 0,1,
тоді частка першого та другого сортів становить
p=l-W=l-0,1 =0,9.
Підставимо дані в формулу для простого випадкового безповторного відбору:
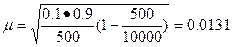
р = 0,9 ±3-0,0131.
Таким чином, на підставі проведеної вибірки встановлено, що середній відсоток виробів третього сорту становить 10 % з можливим відхиленням в той чи інший бік на 3,9 %. З імовірністю 0,997 можна стверджувати, що середній відсоток виробів третього сорту в усій партії буде знаходитись у межах
р = 10% ± 3,9%, тобто 6,1% ÷ 13,9%.
Наведені вище формули середньої та граничної помилки вибірки застосовують при випадковому та механічному відборах.
При типовому відборі гранична помилка визначається за такими формулами (табл. 4.1).
Таблиця 4.1
Граничні помилки вибірки при типовому відборі
| Схема відбору | Гранична помилка вибірки | |
| Для середньої | Для частки | |
| повторний | 
| 
|
| безповторний | 
| 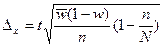
|
Якщо порівняти їх з формулами для випадкового відбору, то виявиться, що замість дисперсії і частки, що визначаються для вибіркової сукупності в цілому, при типовому відборі необхідно обчислити середні з групових дисперсій і частки, що отримані для кожної групи:

Приклад 4.3
Проведена 10-процентна типова вибірка, пропорційна чисельності відібраних груп робітників (табл. 4.2).
Визначити з імовірністю 0,954 межі, в яких знаходиться середній відсоток виконання норм робітниками в цілому. Вибірка безповторна.
Таблиця 4.2
Характеристика вибірки робітників
| Групи робітників за спеціальністю | Чисельність, чол. | Середнє виконання норми,% | Середнє квадратичне відхилення.% |
| Т | |||
| С | |||
| ф |
Обчислимо загальний середній відсоток виконання норми робітниками, які потрапили у вибірку:

Визначимо середню із групових дисперсій:
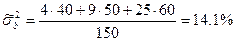
Гранична помилка вибіркової середньої для типового відбору:

Де N = 1 500, так як вибірка 10-процентна.
Таким чином, з імовірністю 0,954 можна стверджувати, що середній відсоток виконання норм робітниками заводу в цілому знаходиться в межах
 = 103,7 ±0,581,
= 103,7 ±0,581,
звідси
103,1 ≤х≤ 104,3.
При серійному відборі з рівновеликими серіями гранична помилка визначається за формулами наведеними в табл. 4.3, де S — загальне число серій у сукупності. У даному випадку кожна серія являється одиницею сукупності, і мірою коливання буде міжсерійна вибіркова дисперсія:

де  — середня для кожної серії;
— середня для кожної серії;  — загальна вибіркова середня, s — число відібраних серій.
— загальна вибіркова середня, s — число відібраних серій.
Таблиця 4.3
Граничні помилки вибірки при серійному відборі
| Схема відбору | Гранична помилка вибірки | |
| Для середньої | Для частки | |
| повторний | 
| 
|
| безповторний | 
| 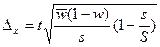
|
Якщо порівняти їх із формулами для випадкового відбору, то виявиться, що замість дисперсії і частки, які визначаються для вибіркової сукупності в цілому, при серійному відборі необхідно обчислити міжгру-пову дисперсію середньої і частки.
Приклад 4.4
Для визначення середньої врожайності цукрового буряка в області проведена 20-процентна серійна вибірка, до якої відійшло 5 районів із 25. Середня врожайність для кожного району становила: 250, 260, 275, 280, 300 ц/га з площі 800, 1000, 1200, 1200 і 2800 га відповідно. Визначити з ймовірністю 0,954 межі, в яких буде знаходитись середня врожайність цукрового буряка по області.
Спочатку знайдемо загальну середню:
 ц/га
ц/га
Визначимо міжсерійну дисперсію:



Розрахуєм граничну помилку серійного безповторного вибору:
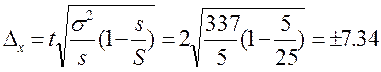 ц/га
ц/га
Отже, з ймовірністю 0,954 можна стверджувати, що середня врожайність цукрового буряка по області буде знаходитись в межах від 272,66 ц/га до 287,34 ц/га. Таким чином розраховуються середня і гранична помилки для частки.
Поиск по сайту: