Характеристики варіації

Варіація ознаки є властивістю статистичної су­купності і зумовлена дією безлічі взаємопов'язаних причин, серед яких є основні і другорядні. Основні формують центр розподілу, другорядні - варіацію оз­нак, сукупна їх дія - форму розподілу [2]. Чим менша варіація, тим більш надійними, типовішими є характе­ристики центру, насамперед середня.

Для характеристики варіації застосовують систему таких оцінок.

Розмах варіації - це різниця між найбільшим і найменшим значенням ознаки R= x_max - x_mln.

В інтервальному ряді розподілу R визначають як різницю між верхньою межею останнього інтервалу і нижньою межею першого або ж різницю між серед­німи значеннями цих інтервалів.

Як міра варіації R не завжди може бути надійним, оскільки залежить від двох крайніх значень, які часто не є типовими для сукупності, або мають випадковий характер. Вони отримали назву «викиди». В практиці статистичних досліджень крайні значення підлягають обробці або, принаймні, уважному розгляданню. Як правило, це помилки кодування або реєстрації, іноді вони мають випадковий характер. Тому їх часто про­сто викидають, звужуючи тим самим розмах і роблячи сукупність більш однорідною. Також зменшує вплив випадкових причин так званий квартальний роз­мах, обчислений за формулою

R_q= Q₃ – Q₁

В усякому разі, відкидаючи крайні значення, слід, пам'ятати, що інколи з ними може бути пов'язане щось цікаве або навіть феноменальне. Замість про­стого відкидання пропонують процедури обчислення оцінок розподілу, які нечутливі до структури даних і отримали назву робастних [1]. Робастними оцін­ками називають також оцінки розподілу, які от­римують при застосуванні цих методів.

Програми статистичних пакетів часто передбачають обчислення оцінок Хампеля, Ендрюса та Т'юки. Наприклад, Т'юки (Tukey) запропонував один з видів робастних оцінок, а саме вінзорізовані оцінки. Суть в тому, що крайні значення не відкидаються а замінюються. Якщо маємо упорядкований ряд зна­чень х₁, х₂,..., х_п, то х₁, надається значення х₂, а х_п -значення х_п-1. Якщо така операція не дає бажаних на­слідків, тобто сукупність ще не стає досить одно­рідною, то процедуру повторюють (наприклад, за до­помогою пакета статистичних програм BMDP до 5 разів). Так, при двократній вінзорізації х₁ та х₂ при­своюється величина варіанти х₃, а двом останнім у ряді — величина х_п-₂.

Важливо підкреслити, що статистичний аналіз від­носиться до таких робіт, де від ретельності підготовки матеріалу може залежати успіх всієї справи. Щодо всіляких процедур «чистки» або попередньої обробки даних, то тут окрім професійного боку справи існує ще й етичний. Дослідник повинен прагнути до об'єк­тивного, науково обгрунтованого результату, а він мо­же виявитись і не таким, як хотілось би.

Середнє відхилення обчислюється як:

1) середнє лінійне відхилення:

а) незважене:

б) зважене:

2) середнє квадратичне відхилення:

а) незважене:

б) зважене:

Характеристика варіації має назву дисперсії:

а) незважена:

б) зважена:

На практиці застосовують більш просту формулу розрахунку дисперсії:

Чим менше середнє відхилення, тим типовіша середня, тим більш однорідна сукупність, а завжди більша за d. В симетричних та помірковано асимет­ричних розподілах = 1,25d. Характеристики R, d та — іменовані величини, які мають одиниці виміру ва­ріюючої ознаки.

При порівнюванні степеня варіації однієї і тієї ж ознаки в різних сукупностях використовують коефіцієнт варіації:

,

Лінійний коефіцієнт варіації:

.

З його допомогою можна оцінити також одно­рідність сукупності. Однорідною прийнято вважати сукупність, для якої V_a < 33%, що приймають до уваги при попередній обробці даних.

Розглянемо особливості обчислення деяких харак­теристик для альтернативної ознаки. Позначимо на­явність ознаки через 1, її відсутність — через 0. Частку одиниць, які мають дану ознаку позначимо через р, які не мають — через q.

Тоді:

,

, або

Очевидно, при відсутності варіації 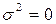; макси­мальне значення дисперсії становить 0,25 при р = q =0,5. Якщо номінальна ознака приймає більше двох значень, оцінка її варіації дорівнює добутку час­ток:

Поиск по сайту: