Аксіоми статики (принципи статики)

1. Аксіома про дві сили (рис. 1.3)

Дві сили, що діють на абсолютно тверде тіло, зрівноважуються тоді і тільки тоді, коли вони діють уздовж однієї лінії в протилежні боки і дорівнюються за модулем.

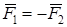
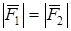
Рис. 1.3

2. Додання (виключення) до діючої на тверде тіло будь – якої зрівноваженої системи сил не змінює дію на тіло, не порушує рівновагу (рис. 1.4).

Рух твердого тіла не зміниться від переносу точки прикладення сили вздовж її лінії дії в будь-яку іншу точку тіла.

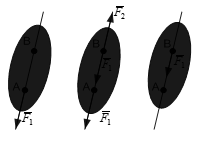
Рис. 1.4

3. Аксіома про паралелограм сил.

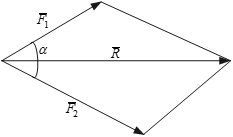
Рівнодійна двох сил, прикладених до тіла в одній точці, дорівнює векторній сумі цих сил і прикладена в тій самій точці (рис. 1.5).

Рис. 1.5

Модуль рівнодійної сили визначається за теоремою косинусів:

.

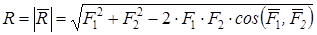Напрямок рівнодійної двох сил визначається діагоналлю паралелограма, побудованого на цих силах.

На основі аксіоми 3 будь-яке число сил, прикладених в одній точці, можна складати геометрично. Рівнодійну сил визначають як векторну суму цих сил (рис. 1.6).

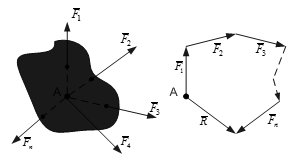
Рис. 1.6

Для цього з кінця вектора, що дорівнює першій силі 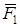, відкидаємо вектор, що дорівнює силі 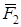, і т.д. З’єднуючи початок першого вектора 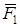з кінцем останнього 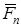, знаходимо рівнодійну силу:

.

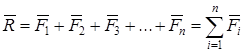Цей многокутник називається многокутником сил, або силовим многокутником.

4. Закон дії і протидії (3-й закон Ньютона).

При деякій дії одного тіла на друге має місце протидія, чисельно рівна, але протилежна за напрямком (рис. 1.7).

Сили дії і протидії 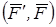дорівнюються за модулем, діють уздовж однієї лінії в протилежному напрямку, але прикладені до різних тіл. Тому сили дії і протидії не врівноважені.

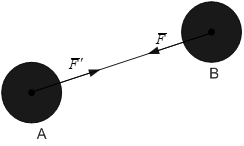
Рис. 1.7

5. Принцип тверднення. Рівновага деформованого (змінюваного) тіла, яке знаходиться під дією даної системи сил, не порушується, якщо його вважати затверділим (абсолютно твердим). Сенс аксіоми полягає в тому, що при вивченні руху деформованих тіл можна користуватися правилами теоретичної механіки, які отримані для твердих тіл.

Система матеріальних точок називається вільною, якщо на рух цих точок не накладено обмежень. У протилежному разі система матеріальних точок називається невільною.

Тіла, або поля, що обмежують свободу руху системи матеріальних точок або твердого тіла, називаються в’язами.

6. Аксіома про звільнення від в’язів. Не змінюючи механічного стану (руху або рівноваги) системи матеріальних точок або твердого тіла, в’язь, накладену на систему або тверде тіло, можна відкинути, замінивши дію в’язі її реакцією, прикладеною до цього тіла або системи в точці взаємодії тіла і в’язі.

Невільні матеріальні точки, систему матеріальних точок або тверде тіло можна розглядати як вільні, якщо їх звільнити від в’язів, заміняючи дію останніх їхніми реакціями.

Поиск по сайту: