Система збіжних сил. Умови рівноваги системи

збіжних сил (рис. 1.20)

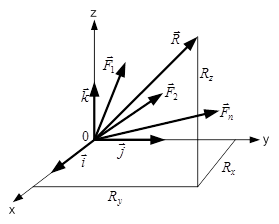
Рис. 1.20

Користуючись аксіомою про паралелограм сил, рівнодійна 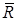системи збіжних сил 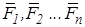визначається графічно як замикальна сторона многокутника сил:

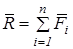
Аналітично рівнодійну силу можна визначити за її проекціями на осі прямокутної системи координат (рис. 1.20) за теоремою про проекції векторної суми на осі координат.

, , ,

де ‑ проекції відповідних сил на осі координат.

Подамо рівнодійну 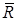у вигляді розкладання по ортах:

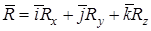
Тоді її модуль ,

або .

Напрямні косинуси рівнодійної сили:

; ; .

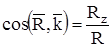Теорема. Для рівноваги просторової системи збіжних сил необхідно і достатньо, щоб рівнодійна сила дорівнювала нулю 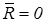. Ця умова є геометричною умовою рівноваги збіжної системи сил.

Оскільки , то многокутник сил має бути замкненим, тобто кінець останньої сили збігається з початком першої сили.

Умови рівноваги системи збіжних сил в аналітичній формі формулюються так: для рівноваги просторової системи збіжних сил необхідно і достатньо, щоб алгебраїчні суми проекцій сил на три взаємно перпендикулярні осі дорівнювали нулю:

; ;

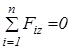
Поиск по сайту: