Рівновага системи тіл

Розглянемо конструкцію, що складається з кількох твердих тіл, з’єднаних між собою за допомогою в’язів. Конструкція, що складається з двох твердих тіл і , з’єднаних між собою за допомогою шарніра , показана на рисунку 3.10. На конструкцію діють сила 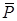, пара сил з моментом і розподілене навантаження інтенсивності 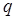. 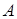У такій конструкції в’язі, з’єднуючи її частини, називаються внутрішніми (шарнір ), а в’язи і 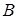- зовнішніми. Реакції в'язів усієї конструкції повністю за допомогою рівнянь рівноваги довільної плоскої системи сил вирішити неможливо, бо кількість невідомих перебільшує кількість рівнянь рівноваги.

До даної конструкції, окрема активних, заданих сил, прикладені реакції зовнішніх в’язів – опор 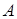і 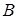. Реакція 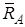шарнірно-рухомого шарніра 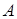перпендикулярна до опорної площини.

З боку опори 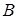, жорсткого защемлення, на конструкцію діють реакція 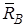невідомого напрямку, що складається з 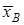і 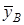, і пара сил . Чотири невідомих реакцій в’язів неможливо визначити з трьох рівнянь рівноваги довільної плоскої системи сил.

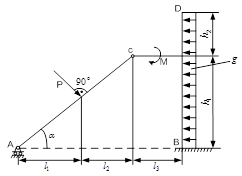
Рис. 3.10

Для їх визначення конструкцію розчленують, розрізають по шарніру на окремі тверді тіла і розглядають рівновагу кожного з них окремо.

Реакції внутрішньої в’язі – шарніра , яка діє на тіло і (рис. 3.11 а, 3.11 б), попарно рівні за модулем і протилежні за напрямком за аксіомою про дію і протидію. Векторним рівнянням і відповідають алгебраїчні рівняння , , що використовуються при розв’язанні задачі. Властивість внутрішніх сил – утворювати зрівноважену систему сил.

а)

б)

Рис. 3.11

Для системи сил, що діють на тіло і тіло , можна скласти ще по три рівняння рівноваги сил, довільно розташованих у площині. З цих шести рівнянь можна визначити шість невідомих .

Тоді розглядувана система сил статично визначена. Рівняння рівноваги конструкції, яка складається з двох твердих тіл, тобто цілком, нерозчленованої, можливо використати для перевірки розв’язання.

Поиск по сайту: