Відносно центра

Векторний момент сили відносно центра 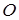дорівнює векторному добутку радіуса вектора точки 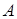прикладення сили відносно цього центра на вектор сили: .

Рис. 2.1

Модуль векторного моменту:

Тут 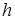‑ плече сили, тобто довжина перпендикуляра, який проведений із центра до лінії дії сили.

Вектор спрямований у той бік, звідки обертаюча дія сили згідно з центром 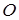видна спрямованою проти ходу годинникової стрілки.

Алгебраїчним моментом сили відносно точки (центра) називається величина, яка дорівнює взятому з відповідним знаком добутку модуля сили на плече: .

Отже, момент сили 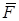відносно центра 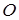чисельно дорівнює добутку модуля сили на плече 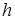і напрямлений перпендикулярно до площини, що проходить через точку 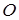і лінію дії сили, в той бік, звідки обертання тіла під дією сили 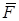навколо точки 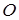(або найкоротший поворот вектора до напряму вектора 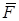) спостерігач бачить таким, що відбувається проти ходу годинникової стрілки. Спостерігач дивиться назустріч вектора-моменту (рис. 2.1, 2.2).

Рис. 2.2

Очевидно, момент сили відносно центра має всі властивості векторного добутку.

Розкриваючи цей визначник за елементами першого рядка і розкладаючи вектор на складові по осях координат, одержимо

.

Порівнюючи ліву й праву частини рівності, маємо аналітичні вирази моменту сили відносно осей :

Ці формули легко одержати, користуючись правилом циклічної перестановки індексів

Модуль і напрям моменту сили відносно центра можна визначити ще так:

,

; ; .

Із визначення моменту сили відносно центра маємо:

1. Якщо перемістити силу вздовж лінії її дії, то момент сили відносно центра не зміниться.

2. Момент сили відносно центра завжди дорівнює нулю, коли лінія дії сили проходить через центр (у цьому випадку плече 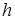дорівнює нулю).

3. Момент сили відносно точки чисельно дорівнює подвоєній площі трикутника (рис. 2.3), побудованого на силі і центрі моменту .

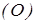Методичні вказівки для визначення моменту сили відносно точки 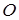(рис. 2.3).

Рис. 2.3

1. Провести лінію дії сили (пряма ).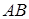

2. З обраної точки 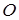провести перпендикуляр на лінію дії сили (довжина перпендикуляра 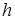- плече сили 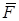відносно центра ).

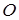3. Скласти добуток модуля сили на плече .

4. Взяти знак “+” якщо сила 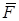прагне обертати площину відносно точки 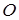проти руху годинникової стрілки, і знак “-” якщо за стрілкою годинника:

.

Теорема про момент рівнодійної просторової системи збіжних сил (теорема Варіньона).

Момент рівнодійної просторової збіжної системи сил відносно довільного центра дорівнює векторній (геометричній) сумі моментів складових сил відносно того самого центра:

.

Рівнодійна 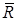збіжної системи сил дорівнює їх геометричній сумі

.

Тоді з визначення моменту сили відносно центру 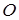маємо

Якщо сили і центр 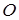розміщені в одній площині, то їхні моменти перпендикулярні до цієї площини і лежать на одній прямій. Тому момент рівнодійної такої системи сил дорівнює алгебраїчній сумі моментів складових сил відносно цієї точки.

Поиск по сайту: