 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Умови рівноваги довільної плоскої системи сил

Рис. 3.7
Система сил  задана у площині
задана у площині 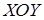 (рис. 3.7). За центр зведення візьмемо довільну точку
(рис. 3.7). За центр зведення візьмемо довільну точку 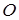 , що належить цій площині. Головний момент
, що належить цій площині. Головний момент  цієї системи сил перпендикулярний до площини
цієї системи сил перпендикулярний до площини 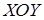 , якій належать сили. Головний вектор
, якій належать сили. Головний вектор  також лежить у площині
також лежить у площині 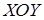 дії сил.
дії сил.
З шести рівнянь рівноваги просторової довільної системи сил залишаються лише три:
1. 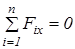 ;
;
2.  ;
;
3. 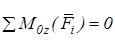 .
.
Для рівноваги довільної плоскої системи сил необхідно і достатньо, щоб алгебраїчні суми проекцій сил на дві взаємно перпендикулярні осі і алгебраїчна сума моментів відносно довільно вибраної точки дорівнювали нулю.
Число невідомих у рівняннях рівноваги для довільної плоскої системи сил не повинно перевищувати трьох, тоді задача буде статично визначеною.
У випадку, якщо вісь 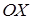 не перпендикулярна до прямої
не перпендикулярна до прямої 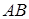 , рівняння рівноваги можна подати у вигляді
, рівняння рівноваги можна подати у вигляді
1. 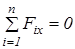 ;
;
2.  ;
;
3. 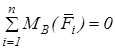 .
.
Якщо три точки 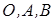 не лежать на одній прямій, всі три рівняння рівноваги можна подати у вигляді рівнянь моментів відносно цих точок:
не лежать на одній прямій, всі три рівняння рівноваги можна подати у вигляді рівнянь моментів відносно цих точок:
1. 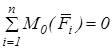 ;
;
2.  ;
;
3. 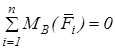 .
.
Такими рівняннями рівноваги довільної плоскої системи сил користуються при визначенні зусиль у стержнях ферми способом Ріттера.
За центр моментів доцільно взяти точку, в якій перетинається найбільша кількість ліній дії невідомих сил (тоді моменти сил відносно цієї точки дорівнюватимуть нулю).
Якщо дві невідомі сили взаємно перпендикулярні, то осі координат доцільно направити по лініях дії цих сил.
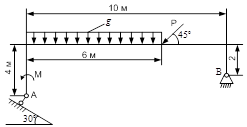
Приклад 1. На рис. 3.8,а показаний брус, вісь якого є ломана лінія. Брус навантажений зосередженою силою  , розподіленим навантаженням постійної інтенсивності
, розподіленим навантаженням постійної інтенсивності  , а також моментом
, а також моментом  . Рівновага навантаженого бруса забезпечується його спиранням в точках
. Рівновага навантаженого бруса забезпечується його спиранням в точках  і
і  на шарнірі (рухомий та нерухомий). Необхідно визначити величини реакцій у шарнірах
на шарнірі (рухомий та нерухомий). Необхідно визначити величини реакцій у шарнірах  і
і 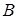 .
.
 а
а
 б
Рис. 3.8
б
Рис. 3.8
| Розв’язання.
Розглянемо рівновагу бруса 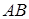 . Обираємо осі . Обираємо осі 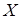 і і  прямокутної системи координат, як показано на рис. 3.8,б. Точку прямокутної системи координат, як показано на рис. 3.8,б. Точку 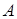 обираємо за початок координат. За аксіомою про звільнення від в’язів замінимо їх дію реакціями: у точці обираємо за початок координат. За аксіомою про звільнення від в’язів замінимо їх дію реакціями: у точці 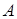 - - 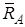 (рухомий шарнір) – реакція перпендикулярна до площини опору, в точці (рухомий шарнір) – реакція перпендикулярна до площини опору, в точці 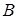 - -  (нерухомий шарнір) – невідома реакція його визначається двома складовими (нерухомий шарнір) – невідома реакція його визначається двома складовими 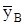 і і 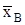 по осях по осях  і і 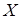 . .
|
Показуємо активні сили і момент. Розподілене на ділянці  навантаження інтенсивності
навантаження інтенсивності 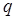 замінимо зосередженою силою
замінимо зосередженою силою  , яка діє посередині ділянки
, яка діє посередині ділянки  і дорівнює
і дорівнює  .
.
Розглянемо систему зрівноважених сил, що діють на брус 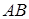 . Для довільної плоскої системи сил складаємо три рівняння рівноваги бруса, користуючись теоремою Варіньйона.
. Для довільної плоскої системи сил складаємо три рівняння рівноваги бруса, користуючись теоремою Варіньйона.
Сума проекцій діючих на брус сил на вісь 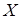 повинна дорівнювати нулю:
повинна дорівнювати нулю:
1. 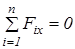 ;
;  .
.
Сума проекцій діючих на брус сил на вісь  повинна дорівнювати нулю:
повинна дорівнювати нулю:
2. 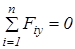 ;
;  .
.
Сума моментів діючих на брус сил відносно точки 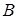 повинна дорівнювати нулю:
повинна дорівнювати нулю:
3.  ;
;

Підставляючи у складені рівняння числові значення величин  , вирішуємо їх відносно невідомих реакцій
, вирішуємо їх відносно невідомих реакцій  :
:
З рівняння 3 маємо
 .
.
З рівняння 2
 .
.
З рівняння 1
 .
.
Знак “-” реакції 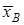 означає, що сила
означає, що сила 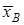 спрямована протилежно показаній на рис. 3.8.
спрямована протилежно показаній на рис. 3.8.
Для перевірки отриманих результатів складемо рівняння суми моментів діючих на брус сил відносно довільної точки (наприклад С):
 ;
; 


Приклад 1 вирішений правильно.
Відповідь:  ,
,  ,
,  .
.
Приклад 2. До балки  , нерухомо закріпленої в точці
, нерухомо закріпленої в точці 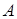 , прикладені сили, як показано на рис. 3.9 а. Дано:
, прикладені сили, як показано на рис. 3.9 а. Дано:  ,
, 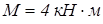 ,
,  Визначити реакції в закріпленні
Визначити реакції в закріпленні 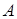 .
.
Розв’язання. Обираємо осі 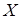 і
і  прямокутної системи координат з початком у точці
прямокутної системи координат з початком у точці 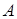 . Розглянемо рівновагу балки
. Розглянемо рівновагу балки  . Побудуємо на схемі зовнішні активні сили і момент, замінив інтенсивність розподіленого на вертикальній ділянці
. Побудуємо на схемі зовнішні активні сили і момент, замінив інтенсивність розподіленого на вертикальній ділянці  навантаження зосередженою силою
навантаження зосередженою силою  . Сила
. Сила  діє посередині ділянки
діє посередині ділянки  . Дію на балку кріплення у точці
. Дію на балку кріплення у точці 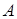 за аксіомою про звільнення від в’язів замінимо їх реакціями (жорстке кріплення) (рис. 3.9,б).
за аксіомою про звільнення від в’язів замінимо їх реакціями (жорстке кріплення) (рис. 3.9,б).
 а а
|  б б
|
Рис. 3.9
Якщо на балку діють сили, то в закріпленні виникають реакції, що складаються з сили реакції закріплення  і пари сил з моментом
і пари сил з моментом  .
.  і
і 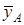 складові реакції
складові реакції 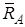 . Напрям реакції
. Напрям реакції 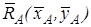 і моменту
і моменту  невідомий.
невідомий.
Розглядаємо систему врівноважених сил, прикладених до балки (активних та реакції в’язів). Рівняння рівноваги в цьому разі матимуть вигляд:
сума проекцій діючих на балку  сил на вісь Х повинна дорівнювати нулю:
сил на вісь Х повинна дорівнювати нулю:
1. 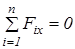 ;
;  ,
,
сума проекцій діючих на балку сил на вісь У повинна дорівнювати нулю:
2. 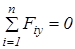 ;
;  ,
,
сума моментів діючих на балку сил відносно точки  мусить дорівнювати нулю:
мусить дорівнювати нулю:
3.  ;
;  .
.
Момент сили  відносно точки
відносно точки  визначається теоремою Варіньйона.
визначається теоремою Варіньйона.
Підставляючи у складені рівняння рівноваги числові значення заданих величин  , вирішуємо їх відносно невідомих реакцій
, вирішуємо їх відносно невідомих реакцій  .
.
З рівняння 1
 .
.
З рівняння 2
 .
.
З рівняння 3
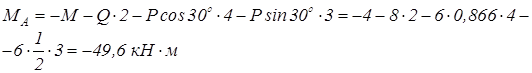
Знак “-” показує, що реакції  спрямовані в протилежний бік.
спрямовані в протилежний бік.
Перевірка. Складемо рівняння суми моментів діючих на балку сил відносно довільної точки  :
:
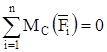 ;
;


 .
.
Оскільки  , то задача про визначення реакцій в защемленні вирішена правильно.
, то задача про визначення реакцій в защемленні вирішена правильно.
Відповідь:  ,
,  ,
,  .
.
Поиск по сайту: