Методичні вказівки для розв’язання задач про рівновагу

Послідовність вирішення задач про рівновагу.

1. Прочитавши умови задачі й виписавши вихідні дані, слід визначити об’єкт дослідження, тобто те тіло, рівновагу якого треба розглянути.

2. Зобразити діючі на тіло активні сили.

3. Маючи на увазі аксіому про звільнення від в’язів, звільнити тіло від в’язів і розглядати його як вільне, але під дією не тільки активних сил, а й реакцій в’язів.

4. Вибрати систему координат.

5. Залежно від характеру одержаної системи сил застосувати відповідні умови рівноваги.

6. Скласти рівняння, розв’язати і проаналізувати їх.

7. Скласти перевірочні рівняння результатів рішення.

Приклад 1. Однорідна куля вагою , що дотикається до гладенької вертикальної стінки, утримується в рівновазі мотузкою (рис. 1.21). Визначити натяг мотузки і тиск кулі на стінку, якщо мотузка із стіною утворює кут .

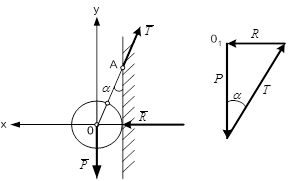
Рис. 1.21

Розв’язання. Оскільки відома сила прикладена до кулі, то розглянемо рівновагу кулі. В’язами для кулі є стінка і мотузка. Оскільки стінка гладенька, то реакція 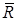буде перпендикулярна до стінки; реакція мотузки має бути спрямована вздовж мотузки до точки підвісу .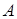

Відкидаємо в’язі та замінюємо їхню дію реакціями. Якщо визначимо реакці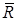ї і , то тим самим знайдемо тиск кулі на стіну й натяг мотузки (це сили протидії й вони напрямлені в бік, протилежний реакціям 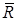і ).

Оскільки сили 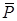, 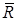і задовольняють теорему про три сили, то для рівноваги кулі необхідно і достатньо, щоб силовий трикутник був замкненим, тобто виконувалась геометрична умова рівноваги збіжних сил.

Для побудови трикутника вибираємо довільну точку і відкладаємо в певному масштабі силу 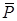. Із її кінця проводимо лінію, що рівнобіжна до лінії дії однієї з реакцій, наприклад . Із умови замкненості силового трикутника кінець сили 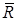має прийти в точку 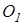. Тому проводимо з 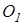лінію, що рівнобіжна силі 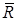. Точка перетину двох ліній єдиним чином визначає величини сил 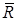і .

Для запису умов рівноваги збіжних сил в аналітичній формі обираємо систему координат .

Записуємо систему алгебраїчних рівнянь:

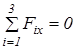; ; . (1)

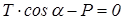; ; . (2)

З рівняння (2) знаходимо

З рівняння (1) знаходимо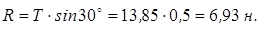

Перевіркою рішення є порівняння результатів, що отримані двома способами.

Відповідь: ,

.

Приклад 2. Тягар ваги підвішений в точці , як зображено на рис.1.22. Кріплення стержнів у точках шарнірне. Знайти реакції в’язів .

Рис. 1.22

Розв’язання.

1. Об’єкт дослідження – точка .

2. Тягар діє з силою на точку .

3. Реакції в’язів спрямовані вздовж ліній, які з’єднують шарніри.

4. Точка знаходиться під дією системи збіжних сил у просторі.

Аналітичні умови рівноваги:

; ; .

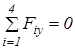5. Складаємо систему алгебраїчних рівнянь:

,

.

Розв’язуючи систему трьох рівнянь відносно трьох невідомих , знаходимо, що , .

Відповідь: , .

Поиск по сайту: