 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Умови рівноваги довільної просторової системи сил
Для рівноваги довільної просторової системи сил (система сил була еквівалентна нулю) необхідно і достатньо, щоб головний вектор і головний момент цієї системи відносно будь-якої точки О дорівнювали нулю, тобто
 ;
;  .
.
Ці умови називаються умовами рівноваги довільної системи сил у векторній (геометричній) формі. Умови рівноваги довільної просторової системи сил в аналітичній формі:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Отже, для рівноваги довільної просторової системи сил необхідно і достатньо, щоб суми проекцій усіх сил на координатні осі та суми моментів цих сил відносно осей координат дорівнювали нулю.
При розв’язуванні задач про рівновагу просторової системи сил, прикладених до твердого тіла, з рівнянь можна визначити шість невідомих величин.
Приклад 1.

Рис. 3.4
На горизонтальний вал (рис. 3.4), що лежить у підшипниках А і D, діють сили 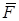 і
і  . Сили
. Сили 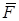 і
і  діють в площині шківів B і C, радіуси яких становлять
діють в площині шківів B і C, радіуси яких становлять  ,
,  . У стані рівноваги сила
. У стані рівноваги сила  , сила
, сила  відхилена від горизонту на кут
відхилена від горизонту на кут  . Дано розміри:
. Дано розміри:  ,
, 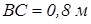 ,
,  . Визначити силу
. Визначити силу 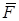 і реакції підшипників А і D, коли
і реакції підшипників А і D, коли  .
.
Розв’язання. Розглянемо рівновагу вала, на який діють активні сили 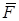 і
і  . В’язами для нього є підшипники А і D. Згідно з аксіомою про в’язі, звільняємо вал від в’язів і замінюємо їх реакціями,
. В’язами для нього є підшипники А і D. Згідно з аксіомою про в’язі, звільняємо вал від в’язів і замінюємо їх реакціями, 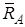 і
і  , що лежать у площинах, перпендикулярних до осі підшипників А і D. Візьмемо систему координат, як показано на рис. 3.4. Невідомі реакції
, що лежать у площинах, перпендикулярних до осі підшипників А і D. Візьмемо систему координат, як показано на рис. 3.4. Невідомі реакції 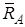 і
і  подаємо складовими
подаємо складовими  , які треба визначити.
, які треба визначити.
Для розв’язання задачі скористаємось умовами рівноваги довільної просторової системи сил в аналітичній формі:
5. 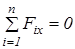 ;
6. ;
6. 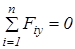 ;
3. ;
3.  ; ;
| 7. 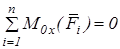 ;
8. ;
8.  ;
6. ;
6.  . .
|
У цьому прикладі друга умова виконується тотожно, оскільки проекції всіх сил, у тому числі реакцій в’язів на вісь  дорівнюють нулю. З п’яти умов рівноваги, що залишилися, слід визначити п’ять невідомих величин:
дорівнюють нулю. З п’яти умов рівноваги, що залишилися, слід визначити п’ять невідомих величин:  – задача статично визначена.
– задача статично визначена.
Щодо заданою задачі умови рівноваги мають вигляд.
9. 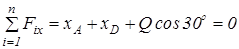 ;
;
10. 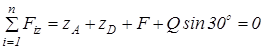 ;
;
11.  ;
;
12.  ;
;
13.  .
.
Звідси з шостої умови
 ,
,
з п’ятої умови
 ,
,
з четвертої умови
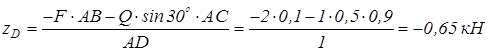 ,
,
з третьої умови
 ,
,
з першої умови
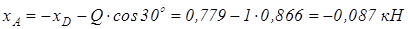 .
.
Відповідь:  ,
,  ,
,  ,
,  ,
,  .
.
Знаки “-” реакцій в’язів  означають, що справжнє напрямлення цих складових протилежне показаним на рисунку.
означають, що справжнє напрямлення цих складових протилежне показаним на рисунку.
Приклад 2.

Рис. 3.5
На горизонтальний вал 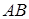 (рис. 3.5) насаджені зубчасте колесо
(рис. 3.5) насаджені зубчасте колесо  радіуса
радіуса  і шестерня
і шестерня  радіуса
радіуса  . До колеса
. До колеса  по дотичній діє горизонтальна сила
по дотичній діє горизонтальна сила  , до шестерні
, до шестерні  по дотичній діє вертикальна сила
по дотичній діє вертикальна сила 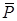 . Дано розміри:
. Дано розміри:  ,
,  ,
,  . Визначити силу
. Визначити силу  і реакції підшипників
і реакції підшипників 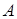 і
і 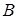 в рівновазі.
в рівновазі.
Розв’язання. Розглянемо рівновагу вала разом з зубчастим колесом  і шестернею
і шестернею  . В’язами для нього є підшипники
. В’язами для нього є підшипники 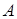 і
і 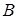 . Звільнимо вал від в’язів, невідомі реакції в’язів
. Звільнимо вал від в’язів, невідомі реакції в’язів 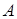 і
і 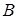 подамо складовими. Невідомі складові лежать у площинах, перпендикулярних до осі підшипників -
подамо складовими. Невідомі складові лежать у площинах, перпендикулярних до осі підшипників - 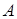 ,
, 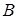 . Обираємо систему координат, як показано на рис. 3,5, тобто в точці
. Обираємо систему координат, як показано на рис. 3,5, тобто в точці 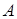 початок координат. Тоді невідомими реакціями в’язів є
початок координат. Тоді невідомими реакціями в’язів є  , які і треба визначити.
, які і треба визначити.
У цьому прикладі з шести умов рівноваги довільної просторової системи сил залишиться також п’ять рівнянь, тому що перша умова виконується тотожно – проекції усіх сил на вісь Ах дорівнюють нулю.
З п’яти умов рівноваги слід визначити п’ять невідомих величин:  і
і  - задача статично визначена.
- задача статично визначена.
Умови рівноваги вала 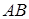 :
:
14.  ;
;
15.  ;
;
16.  ;
;
17.  ;
;
18. 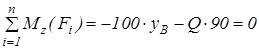 .
.
Звідси
 ;
;
 ;
;
 ;
;
 ;
;
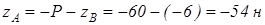 .
.
Відповідь:  ,
,  ,
,  ,
,  ,
,  .
.
Реакції  - спрямовані у напрямку, протилежно визначеному на рисунку.
- спрямовані у напрямку, протилежно визначеному на рисунку.
Поиск по сайту: