Аксіоми статики

Статика базується на декількох вихідних положеннях (аксіомах), які беруться без математичних доказів.

Аксіома 1 (про рівновагу системи двох сил).

Для рівноваги системи двох сил необхідно і достатньо, щоб ці сили були рівні за модулем і діяли уздовж однієї прямо в протилежних напрямках (рис.1.2), тобто

Цією аксіомою встановлюється найпростіша зрівноважена система сил.

Аксіома 2 (про приєднання та відкидання зрівноваженої системи сил).

Дія даної системи сил на абсолютно тверде тіло не зміниться, якщо до неї приєднати або від неї відкинути зрівноважену систему сил.

Ця аксіома встановлює еквівалентність двох систем сил, які відрізняються на зрівноважену систему сил.

Наслідок із аксіом 1 і 2.

Дія сили на тверде тіло не зміниться, якщо силу перенести вздовж лінії її дії в будь-яку точку тіла.

Для доведення наслідку розглянемо силу A F, прикладену в точці А (рис. 1.3,а). У точці В на лінії дії сили прикладемо зрівноважену систему сил

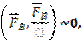
Тоді відповідно до аксіоми 2 одержимо:

(рис. 1.3,б). Згідно з аксіомою 1 система сил 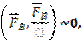а згідно з аксіомою 2 їх можна відкинути (рис. 1.3,в), тобто. Таким чином, наслідок доведено.

З цього наслідку можна зробити висновок, що сила є ковзним вектором.

Аксіома 3 (про паралелограм сил).

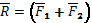
Модуль рівнодіючої знаходять як величину діагоналі паралелограма, побудованого на силах, як на сторонах:

де a – кут, утворений напрямками сил і .

Якщо сили і направлені вздовж однієї прямої в одному або протилежних напрямках, то векторне складання переходить в алгебраїчне.

Напрямок рівнодіючої можна визначити кутами і , які вона утворює із складовими силами і :

Очевидно, що будь-яку силу , взявши її як рівнодіючу, можна розкласти за правилом паралелограма на дві складові сили і ., які утворюють кути і з напрямком цієї сили (рис. 1.4). Величини складових слід визначати за формулами:

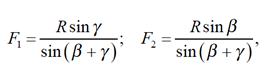
які витікають із попередніх формул.

Аксіома 4 (про рівність сил дії і протидії).

Сили взаємодії двох тіл рівні за величиною і напрямлені вздовж однієї прямої в протилежних напрямках (рис. 1.5).

Хоч сили (рис. 1.5) взаємодії двох тіл і відповідно умовам аксіоми 1 = , але вони не створюють зрівноважену систему сил, бо вони прикладені до різних тіл.

Аксіома 5 (принцип затвердіння).

Рівновага тіла, яке деформується, не порушиться, якщо його вважати абсолютно твердим.

Ця аксіома дозволяє застосовувати методи статики абсолютно твердого тіла для тіл, які деформуються, та змінних конструкцій, вважаючи їх абсолютно жорсткими.

Але хибним буде твердження про те, що рівновага твердого тіла обов’язково збережеться, якщо воно перестане бути твердим.

Поиск по сайту: