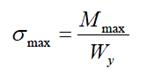Нормальні напруження при згині
Вже відзначалося, що нормальні та дотичні напруження, які одночасно можуть виникати в нормальному до осі перерізі балки, пов’язані з моментами та перерізаючою силою відповідно. Розглянемо випадок так званого чистого згину, який виникає на ділянці за умов Q = 0 та M = const. Такий випадок можна відтворити, наприклад, при навантаженнях балок, зображених на рис. 3.10, а та б. На ділянках CD цих балок виникає чистий згин (епюри моментів М(х) на цих ділянках затемнені).
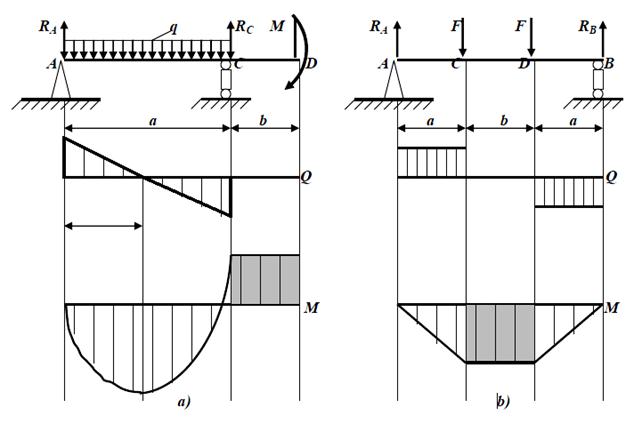
Рисунок 3.10 – Випадки чистого згину: а) на консолі, б) для ділянки між опорами
Для виведення формул нормальних напружень при згині σ домовимося розглядати випадок чистого згину.
Розглянемо ділянку балки довжиною dx, яка знаходиться під дією чистого згину (рис. 3.11). При цьому направимо вісь x уздовж балки, вісь y пов’яжемо з шаром, який не деформується (не стискається і не розтягується). Його називають нейтральним шаром. Вісь z поєднаємо з висотою перерізу.
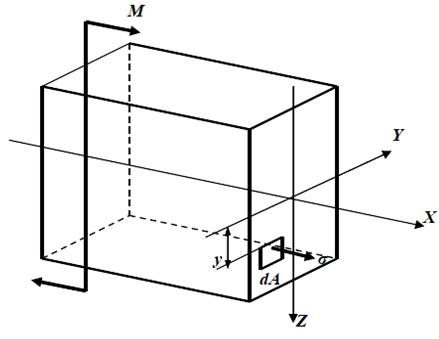
Рисунок 3.11 – Напружений елемент балки
Описуючи статику цієї ділянки, матимемо:

Оскільки розподіл σ по висоті перерізу невідомий, задача носить статично невизначений характер. Тому слід розглянути деформацію цієї ділянки (рис. 3.12).
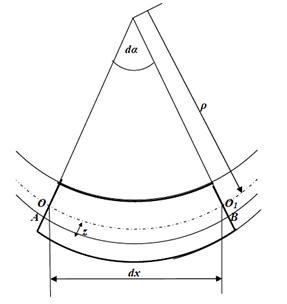
  Рисунок 3.12 – Деформація елементів довжиною dx Рисунок 3.12 – Деформація елементів довжиною dx
 Якщо розглянути найбільші напруження в перерізі (рис. 3.13), то слід відзначити, що вони виникають у найвіддаленіших від нейтральної осі шарах (| z |= z max). Якщо розглянути найбільші напруження в перерізі (рис. 3.13), то слід відзначити, що вони виникають у найвіддаленіших від нейтральної осі шарах (| z |= z max).
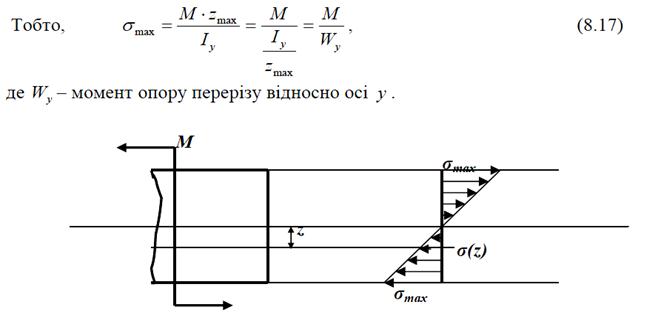
Рисунок 3.13 – Розподіл нормальних напружень по висоті перерізу
Повертаючись до питання знаходження max нормальних напружень max σ у балці, слід ще знати небезпечний переріз, тобто той, де M = M max, тоді
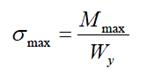
Використовуючи (3.11), неважко записати умову міцності за нормальними напруженнями при згині:

З цієї формули за відомими моментами M та знаючи допустимий рівень напружень [σ ], можна визначити осьовий момент опору y W (а далі і розміри відповідного перерізу) або за відомими формою та розмірами перерізу підібрати допустимі силові фактори, якими можна навантажити балку. При цьому значення M max підбирають при побудові епюр Q (х) та M (х).
Практика показала, що в більшості випадків найнебезпечнішими для балок є нормальні напруження. Тому залежності (3.10 ÷ 3.12) є дуже важливими розрахунковими формулами. Дослідження показали, що формули (3.10 ÷ 3.12) практично справедливі не тільки для випадку чистого згину, але й у випадку, коли на ділянці, що розглядається, перерізаюча сила Q не дорівнює нулю. Похибка незначна і можна вважати формули (3.10 ÷ 3.12) універсальними при розгляді плоского згину прямого бруса.
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | Поиск по сайту:
|






 Рисунок 3.12 – Деформація елементів довжиною dx
Рисунок 3.12 – Деформація елементів довжиною dx
 Якщо розглянути найбільші напруження в перерізі (рис. 3.13), то слід відзначити, що вони виникають у найвіддаленіших від нейтральної осі шарах (| z |= z max).
Якщо розглянути найбільші напруження в перерізі (рис. 3.13), то слід відзначити, що вони виникають у найвіддаленіших від нейтральної осі шарах (| z |= z max).