Рекурентна форма математичної моделі руху судна (за методом кінцевих різниць) та сформувати початкові та граничні умови

Метод різницевої апроксимації є ітераційним, тобто покроковим. Сутність його полягає в тому, що диференційне рівняння замінюється різницевим.

Для цього 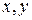- представляємо у вигляді відрізків (а тобто яких-небудь значень). Розіб’ємо ці відрізки на N рівних частин точками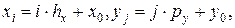

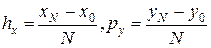- кроки.

Будуємо сіточну область з просторовим кроками: 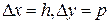, та часовим .

Похідна 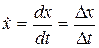замінюється різницевим аналогом:

- висхідна різниця;

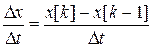- низхідна різниця;

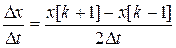- центральна різниця,

де .

Друга похідна замінюється:

Якщо прийняти 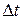=1, отримаємо для різниці, n – го порядку

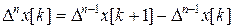
чи безпосередньо через значення різницевої функції [1]

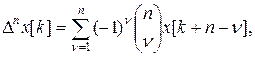
де - біноміальні коефіцієнти.

При дослідженні неперервних систем n – порядку

використовують рівняння, які визначаються зв’язком між безперервною функцією та її похідними.

При переході до різницевих рівнянь будемо мати

,

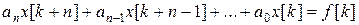де - відома функція;

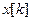- розв’язок різницевого рівняння.

Різницеве рівняння n –гопорядку відповідає безперервному диференційному рівнянню n –гопорядку. Диференційне рівняння можливо розглядати як граничне для різницевого, якщо прийняти період дискретності прямує до нуля.

Будуємо рекурентну форму математичної моделі руху судна у середовищі MATLAB за висхідною різницею.

b(i+1)=(r11*w(i)+q11*b(i)+s11*Vx(i)*a(i))*t+b(i);

w(i+1)=(r21*Vx(i)*w(i)+q21*Vx(i)*b(i)+s21*Vx(i)*Vx(i)*a(i))*t+w(i);

psi(i+1)=w(i)*t+psi(i);

phi(i+1)=((psi(i+1)-psi(i))-(b(i+1)-b(i)))+phi(i);

Vx(i+1)=V*sin(phi(i+1));

Vy(i+1)=V*cos(phi(i+1));

x(i+1)=x(i)+Vx(i+1)*t;

y(i+1)=y(i)+Vy(i+1)*t;

if (0<175.3)

psiz= 3.9095;

end;

if (175.3>291)

psiz=3.8921;

end;

if (291>370)

psiz=3.3336;

end;

a(i+1)=k1*(psi(i+1)-psiz)+k2*w(i);

Поиск по сайту: