 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Еквівалентність формальних моделей алгоритмів
Обмежимося розглядом п- арних функцiй на множині N.
Теорема 1. Клас ЧРФ збігається з класом програмованих на N п-арних функцiй.
1) ЧРФ Í програмованi на N. Базовi функцiї о, s, I 
програмованi на N. Залишається показати, що функцiї, отриманi iз програмованих за допомогою операцiй R та M, теж програмованi. Зрозуміло, що функцiї +, ´ 
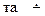програмованi. Згiдно з теоремою про представлення операцiї R досить показати, що якщо функцiя g програмована, то й функцiя f = M (g) програмована. Але операцiя M - по сутi частковий випадок операцiї циклу. У випадку (п +1)-арної функції g операторний терм ППА-Ar- N для f = M (g) має вигляд S n +2(N ☼ (S n +2(g, I 
,..., I 
, I 
), S 2(s, I )), о п, I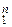 
,..., I 
).
2) Програмованi на N Í ЧРФ. Базовi програмованi на Nп- арніфункцiї о, s, I , +, ´ 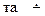є ЧРФ. Залишається показати, що якщо функцiї a та f - ЧРФ, то й функцiя N ☼ (a, f) - ЧРФ. Нехай маємо ЧРФ a(x 1 ,..., xn) та f (x 1 ,..., xn). Розглянемо тепер функцiю j(x 1, ..., xn, у) - по суті y -кратну iтерацiю функцiї f по x 1, що задається такою схемою примiтивної рекурсiї:
j(x 1, ..., xn, у) = x 1;
j(x 1, ..., xn, k+ 1) = f (j(x 1, ..., xn, k), x 2, ..., xn).
Отже, j можна подати у виглядi R (g, h), де g та h - суть функцiї g (x 1 ,..., xn)= x 1 і h (x 1, ..., xn, у, z) = f (z, x 2,..., xn). Операторний терм алгебри ЧРФ для функції j має вигляд R (I 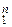, S n +1(f, I 
, I 
,..., I 
)). Звiдси для функції N ☼ (a, f) маємо:
N ☼ (a, f)(x 1 ,..., xn)= j(x 1, ..., xn,m y (a(j(x 1, ..., xn, у), x 2, ..., xn)=0)).
Таким чином, N ☼ (a, f) - ЧРФ.
Теорема 2. Кожна ЧРФ - МНР-обчислювана функцiя.
Базовi функцiї о, s, I обчислюванi такими МНР-програмами:
- програма 1) Z (0) для функцiї о;
- програма 1) S (0) для функцiї s;
- програма 1) T (m -1, 0) для функцiї I .
Нехай k -арна функцiя g та n -арнi функцiї g 1,..., gk обчислюванi вiдповiдно МНР-програмами G, G 1,..., Gk. Тодi функцiя S n +1(g, g 1,..., gk) обчислюється МНР-програмою такого вигляду (тут m = max (r(G),r(G 1),...,r(Gk))):
T (j, m + j +1) для всіх j Î{0,..., n -1}
Gj [ m +1,..., m + n → m + n + j ] для всіх j Î{0,..., n -1}
G [ m + n +1,..., m + n + k → 0].
Нехай (n +1)-арна функцiя g обчислювана МНР-програмою G. Тодi функцiя M (g) обчислюється МНР-програмою такого вигляду (тут m =r(G)):
T (j, m + j +1) для всіх j Î{0,..., n -1}
p) G [ m +1,..., m + n +1→ 0]
J (0, m + n +2, q)
S (m + n +1)
J (0, 0, p)
q) T (m + n +1, 0).
Нехай n -арна функцiя g та (n +2)-арнa функцiя h обчислюванi вiдповiдно МНР-програмами G і H. Тодi функцiя R (g, h) обчислюється МНР-програмою такого вигляду (тут m = m a x (r(G),r(H)):
T (j, m + j +1) для всіх j Î{0,..., n }
p) G [ m +1,..., m + n → m + n +3]
J (m + n +1, m + n +2, q)
H [ m +1,..., m + n +2, m + n +3→ m + n +3]
S (m + n +2)
J(0, 0, p)
q) T (m + n +3, 0).
Отже, кожна ЧРФ - МНР-обчислювана функцiя.
Правильне i зворотне твердження:
Теорема 3. Кожна МНР-обчислювана функцiя є ЧРФ.
Дамо iдею доведення. Нехай f (x 1, ..., xn) обчислюється МНР-програмою P. Позначимо r(x 1, ..., xn, t) функцiю, значенням якої є вмiст 0-го регiстра пiсля t крокiв роботи P над x 1, ..., xn, або пiсля q £ t крокiв, якщо на q -му кроцi програма P при роботi над x 1, ..., xn зупинилась. Через w(x 1, ..., xn, t) позначимо функцiю, значенням якої є номер команди пiсля t крокiв роботи P над x 1, ..., xn, або 0, якщо програма P при роботi над x 1, ..., xn зупинилась на кроцi q £ t. Моделюючи роботу P над x 1, ..., xn за t крокiв, можна довести примiтивну рекурсивнiсть функцiй r та w. Але
f (x 1, ..., xn)= r(x 1, ..., xn,m t (w(x 1, ..., xn, t)=0)),
тому f є ЧРФ.
Наслiдок 1. Клас ЧРФ збігається з класом МНР-обчислюваних функцiй.
Ураховуючи результат теореми 1, маємо:
Наслiдок 2. Класи ЧРФ, МНР-обчислюваних функцiй та програмованих на N функцiй збігаються.
За кожною МТ можна збудувати еквiвалентний їй НА, який задає те ж вербальне вiдображення. З іншого боку, за кожним НА можна збудувати еквiвалентну йому МТ. Отже:
Твeрджeння 1. Клас МТ-обчислюваних функцiй збігається з класом НА-обчислюваних функцiй.
Ще в 1937 р. А.Тьюрiнг установив:
Твeрджeння 2. Клас МТ-обчислюваних функцiй збігається з класом ЧРФ.
Має мiсце також наступне твердження:
Твeрджeння 3. Клас функцiй, обчислюваних за Постом, збігається з класом НА-обчислюваних функцiй.
Пiдсумовуючи зазначені результати, дiстаємо:
Теорема 4. Наступнi класи функцiй збігаються:
1) клас ЧРФ;
2) клас програмованих на N п-арних функцiй;
3) клас МНР-обчислюваних функцiй;
4) клас функцiй, обчислюваних за Тьюрiнгом;
5) клас функцiй, обчислюваних за Марковим;
6) клас функцiй, обчислюваних за Постом.
Розглянутi нами вище формалiзми задають один i той же клас п- арнихфункцiйна N. При цьому самi визначення формалiзмiв такi, що забезпечують ефективну обчислюванiсть описуваних ними функцiй. Тому є всi пiдстави вважати, що такi формалiзми є рiзними математичними уточненнями iнтуїтивного поняття алгоритмiчно обчислюваної функцiї (АОФ). Уперше таке твердження стосовно рекурсивних функцiй було висунуте в 1936 роцi А. Чорчем, тому дiстало назву ” теза Чорча ”. В цьому ж роцi С. Клiнi узагальнив тезу Чорча на випадок часткових функцiй. Розглянемо тезу Чорча в розширеному виглядi.
Поиск по сайту: