 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Алгебри ЧРФ та ПРФ
|
Читайте также: |
Алгебра (Â; R, M, S2, S 3,...), носiєм Â якої є клас усiх ЧРФ, а операцiями – операцiї R, M та S n +1, де n ³1, називається алгеброю ЧРФ, або алгеброю Чoрча.
Алгебра (Â pr ; R, S 2, S 3,...), носiєм Â pr якої є клас усiх ПРФ, а операцiями - операцiї R та S n +1, де n ³1, називається алгеброю ПРФ.
Уведемо поняття операторного терма алгебри ЧРФ та операторного терма алгебри ПРФ. Алфавiт складатиметься iз символiв базових функцiй о, s та I 
, де n ³ m ³1, символiв операцiй R, M та S n +1, де n ³1, а також допомiжних символiв (,) та,.
Дамо iндуктивне визначення ОТалгебри ЧРФ:
1) кожен символ базової функцiї є ОТ; такі ОТ назвемо атомарними;
2) якщо t 0, t 1,..., tn - ОТ, то S n +1(t 0, t 1,..., tn) - ОТ;
3) якщо t 1 та t 2 - ОТ, то R (t 1, t 2) - ОТ;
4) якщо t - ОТ, то M (t) - ОТ.
Аналогiчно дається індуктивне визначення ОТ алгебри ПРФ.
Кожна ЧРФ є значенням деякого ОТ алгебри ЧРФ. Проте не кожен ОТ алгебри ЧРФ має певне значення. Наприклад, операторнi терми R (о, I 
) та S 3(I 
, I 
, I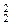 
) не мають значення.
Зауважимо, що завдання ЧРФ операторними термами не є однозначним. Наприклад, операторнi терми о, S 2(о, s), S 2(о, о) та S 2(о, S 2(о, s)) задають одну i ту ж функцiю о (x).
Розглянемо приклади ПРФ, ЧРФ та РФ.
Приклад 1. Функцiї-константи - ПРФ.
Справді, n -арна нуль-функцiя о n (x 1 ,...,xn)=0 задається ОТ S 2(о, I 
);
n -арна константа k n (x 1 ,...,xn)= k задається ОТ S 2(s, S 2(s,..., S 2(о, I )...).
Приклад 2. Функцiя f (x 1, x 2)= x 1+ x 2 - ПРФ. Справдi, маємо
f (x 1, 0) = x 1 = I 
(x 1);
f (x 1, x 2+1) = x 1 + (x 2+1) = (x 1 +x 2) + 1 = s (x 1 +x 2)= s (f (x 1, x 2)).
Отже, функцiя f (x 1, x 2)= x 1+ x 2 виникає примiтивною рекурсiєю iз функцiй g (x 1)= I (x 1) та h (x 1, x 2, x 3)= x 3+1= s (x 3)= S 2(s, I 
)(x 1, x 2, x 3).
Операторний терм функцiї x 1+ x 2 має вигляд R (I , S 2 (s, I )).
Приклад 3. Функцiя f (x 1, x 2)= x 1× x 2 - ПРФ. Справдi, маємо
f (x 1, 0) = 0 = о (x 1);
f (x 1, x 2+1) = x 1×(x 2+1) = x 1× x 2+ x 1 = f (x 1, x 2) +х 1.
Отже, функцiя f (x 1, x 2)= x 1× x 2 виникає примiтивною рекурсiєю iз функцiй g (x 1)= о (x 1) та h (x 1, x 2, x 3) = x 3 +x 1. За прикладом 2 функцiя h є ПРФ, тому f - ПРФ. Операторний терм Ä функцiї x 1× x 2 має вигляд
R (о,S 3(Å, I , I 
)),
де Å - операторний терм функцiї x 1+ x 2 .
Приклад 4. Функцiя f (x 1, x 2) = 
- ПРФ. Справдi, маємо
f (x 1, 0) = (x 1)0 = 1;
f (x 1, x 2+1) = 
= × x 1 = f (x 1, x 2)× х 1 .
Отже, функцiя f (x 1, x 2)= виникає примiтивною рекурсiєю iз функцiй g (x 1) = 1 1(x 1) та h (x 1, x 2, x 3) = x 3× x 1. За прикладом 3 функцiя h є ПРФ, тому f - ПРФ. Операторний терм функцiї має вигляд R (S 2(s, о), S 3(Ä, I , I )), де Ä - ОТ функцiї x 1× x 2 .
Приклад 5. Функцiя sg (x 1)= 
- ПРФ.
Справдi, маємо
sg (0)= 0 = о (x 1);
sg (x 1+1) = 1.
Операторний терм функцiї sg (x 1) має вигляд R (о, S 2(s, S 2(о, I ))).
Приклад 6. Функцiя пsg (x 1) = 
- ПРФ.
Справдi, маємо
пsg (0)= 1 = s (о (x 1));
пsg (x 1+1) = 0.
Операторний терм функцiї пsg (x 1) має вигляд R (S 2(s, о), S 2(о, I )).
Приклад 7. Функцiя f (x 1, x 2) = 
= 
є ПРФ.
Спочатку покажемо, що функцiя 
- ПРФ. Справдi, маємо
= 0 = о (x 1);
= x 1 = I (x 1, x 2).
Операторний терм функцiї 
має вигляд R (о, I ).
Тепер покажемо, що функцiя f (x 1, x 2)= 
- ПРФ. Маємо
f (x 1, 0) = 
= I (x 1);
f (x 1, x 2+1) = 
= 
= 
.
Отже, функцiя f (x 1, x 2) = виникає примiтивною рекурсiєю iз функцiй g (x 1)= I 
(x 1) та h (x 1, x 2, x 3)= 
. Звідси операторний терм функцiї має вигляд R (I , S 2(R (о, I ), I )).
Приклад 8. Функцiя f (x 1, x 2) = | x 1- x 2| = (
)+(
) - ПРФ.
Приклад 9. Функцiя f (x 1, x 2) = x 1- x 2 = 
(| x 1-(x 2 +x 3)|=0) - ЧРФ.
Приклад 10. Всюди не визначена функцiя f Æ - ЧРФ. ×
Cправді, f Æ(x 1)= 
(x 1+1=0), тому f Æ є значенням ОТ М (s).
Приклад 11. Функцiя f (x 1, x 2) = [ x 1 /x 2] - ЧРФ. ×
Cправді, [ x 1 /x 2] = 
(x 2 ×(x 3+1)> x 1) = (nsg (x 2 ×(x 3+1) 
)=0).
Функцiя [ x 1 /x 2] не визначена при x 2=0, тому вона не РФ і не ПРФ.
Приклад 12. Функцiя f (x 1) = [ 
] - РФ. Справді, [ ] тотальна й [ 
]= 
((x 2+1)×(x 2+1)> x 1)= (nsg ((x 2+1)×(x 2+1) )=0).
Розглянемо деякi елементарнi властивостi ПРФ i РФ. Для спрощення звичайно позначатимемо xn +1 та xn +2 як у і z відповідно.
Теорема 1. Нехай (n+ 1) -арна функцiя g - ПРФ. Тодi (n+ 1) -арна функцiя f, задана умовою f (x 1 ,...,xn, у) =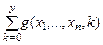 
, також ПРФ.
Домовимося надалi вважати, що при z<y 
= 0.
Тeорeма 2. Нехай (n+ 1) -арна функцiя g - ПРФ. Тодi (n+ 2) -арна функцiя f, задана умовою f (x 1 ,...,xn,у,z) = 
, також ПРФ.
Тeорeма 3. Нехай (n+ 1) -арна функцiя g та n-арнi функцiї a i b - ПРФ. Тодi n-арна функцiя h, задана умовою h (x 1 ,...,xn)= 
, - також ПРФ.
Теореми 1-3 називають теоремами сумування. Замiнивши в цих теоремах символ суми S на символ добутку P, одержимо теореми мультиплiкацiї.
Кажуть, що (п +1)-арна функцiя f отримується iз (n+ 1)-арної функцiї g за допомогою операцiї обмеженої мiнiмiзацiї, якщо вона задається таким спiввiдношенням:
f (x 1 ,...,xn, у)=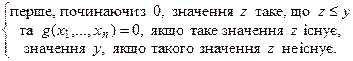 
Цей факт позначаємо так: f (x 1 ,..., xn, у) = 
((g (x 1 ,..., xn, z)=0).
Тeорeма 4 (про обмeжeну мiнiмiзацiю). Нехай (n+ 1) -арна функцiя g є ПРФ. Тодi (n+ 1) -арна функцiя f, задана умовою
f (x 1 ,...,xn, у) = ((g (x 1 ,..., xn, z)=0)- також ПРФ.
Наслідок. Нехай функцiї g (x 1 ,..., xn, у) та a (x 1 ,..., xn) є ПРФ. Тодi функцiя f (x 1 ,..., xn) = 
((g (x 1 ,..., xn, у)=0) також є ПРФ.
Приклад 13. Довизначимо функцiю f (x 1, x 2) = [ x 1 /x 2] таким чином: [ x 1 /0 ]= x 1. Тоді функцiя [ x 1 /x 2] є ПРФ. Справдi, значення [ a/b ] рiвне кiлькостi нулiв у послiдовностi 1× 
, 2× ,..., a × . Тому [ x 1 /x 2] = 
), звідки [ x 1 /x 2] є ПРФ за теоремою 3.
Приклад 14. Функцiя mod (x 1, x 2) - остача вiд дiлення x 1 на x 2 - є ЧРФ. Справдi, mod (x 1, x 2) = 
×[ x 1 /x 2]).
Зауважимо, що, беручи тут довизначену функцію [ x 1 /x 2], дістанемо довизначену функцію mod (x 1, x 2): mod (x 1,0)=0. Така довизначена функція mod (x 1, x 2) є ПРФ.
Приклад 15. Функцiя f (x 1) = [ 
] є ПРФ.
Маємо [ ]= 
(nsg ((x 2+1)×(x 2+1) 
)=0), тому за теоремою 6.6.4 [ ] є ПРФ.
Приклад 16. Функцiя пd (x) - кількість дiльників числа x - є ПРФ при довизначенні пd (0)=1. Справдi, пd (x) = 
.
Приклад 17. Функцiя p(x) - кількість простих чисел, які не більші за число x, є ПРФ. Справдi, p(x) = 
Приклад 18. Функцiя р (x) - х -ве просте число, є ПРФ (тут р (0)=2, р (1)=3 і т.д.)
Справдi, р (x)=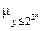 
(| p(у)-(x +1)|=0). Доведення того факту, що р (x) 
, проведемо індукцією по х. Для х =0 маємо р (0)=2 
. Нехай для всіх х £ k маємо p (x) 
. Покажемо p (k +1) 
. Розглянемо число b = p (0)× p (1)× … × p (k)+1. За припущенням індукції р (0) , …, p (k) 
. Тому b 
. Але кожний простий дільник числа b більший за p (k), тому p (k +1)£ b 
.
Приклад 19. Функцiя ex (x, y) - степінь числа р (x) у числі у - є ПРФ при довизначенні ех (x, 0)=0.
Справдi, ex (x, y) = m z £ y (nsg (mod(y, p (x) z +1))× sg (y)=0).
ЛЕКЦІЯ 5
ПЛАН
1. Програмні алгебри. Примітивні програмні алгебри.
2. Програмовані функції.
Поиск по сайту: