 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Програмні алгебри. Примітивні програмні алгебри
Програмна алгебра (P, C) задається парою (B, C), де множина функцій P - основа алгебри, C - множина композицiй (операцiй) над функцiями із P, B Í P - множина базових функцiй. Примiтивні програмні алгебри (ППА) - це програмнi алгебри функцiй із простими типами даних. До таких функцiй належать, зокрема, квазіарні, Х- арні та п- арніфункцiї, заданi на неструктурованих множинах (наприклад, на множині N, на множинi R). Kомпозицiями ППА є операцiї суперпозицiї, циклу і розгалуження.
Операцiї суперпозицiї - це описані вище операцiї S 
.
Для випадку п -арних функцій N операцiї суперпозицiї, циклу й розгалуження дамо наступним чином.
Операцiя циклу N ☼ n -арним функціям g та a ставить у вiдповiднiсть n -арну функцiю f, значення f (x 1 ,..., xn) якої для кожного набору значень x 1 ,..., xn визначається як перший елемент аm послідовності
a 0= x 1, a 1= f (a 0, x 2, ..., xn), a 2= f (a 1, x 2, ..., xn),..., ak = f (ak -1, x 2, ..., xn),...
такий, що a(am, x 2, ..., xn)=0 та для всiх k<m значення a(ak, x 2, ..., xn) визначене і ¹0, якщо такий елемент am iснує. Якщо такий елемент am не iснує, значення f (x 1 ,..., xn) не визначене.
Операцiя розгалуження N D n -арним функцiям g, h і a ставить у вiдповiднiсть n -арну функцiю f, значення f (x 1 ,..., xn) якої для кожного набору значень x 1 ,..., xn визначається так:
f (x 1 ,..., xn) = 
Базовими функцiями для випадку n -арних функцiй, заданих на множинi N, будемо вважати функцiї о, s та I 
, де n ³ m ³1, а також бінарні функції +, × 
.
2. Програмовані функції
Функцiю назвемо програмованою на N, якщо її можна отримати iз указаних вище базових функцiй за допомогою скiнченної кiлькостi застосувань операцiй суперпозицiї S n +1, розгалуження N D, циклу N ☼.
Із наведених визначень випливають наступні твердження:
1. Якщо функцiї a, g, h алгоритмiчно обчислюванi, то функцiя N D (a, g, h) алгоритмiчно обчислювана.
2. Якщо функцiї a та g алгоритмiчно обчислюванi, то функцiя N ☼ (a, g) алгоритмiчно обчислювана.
3. Кожна програмована на N n-арна функцiя є алгоритмiчно обчислюваною.
Алгебра (Ã N; N D, N ☼, S2, S3,...), носiєм Ã N якої є клас усiх програмованих на N n -арних функцiй, а операцiями - операцiї N D, N ☼ та S n +1, де n ³1, називається примiтивною програмною алгеброю програмованих на N n-арних функцiй (ППА-Ar- N).
Дамо індуктивне визначення операторного терма ППА-Ar-N (ОТ ППА-Ar- N). Алфавiт складатиметься iз символiв базових функцiй о, s +, ´ 
та I 
, де n ³ m ³1, символiв операцiй N D, N ☼ і S n +1, де n ³1, а також допомiжних символiв (,) та,.
1) кожен символ базової функцiї є ОТ; такі ОТ назвемо атомарними;
2) якщо t 0, t 1,..., tn - ОТ, то S n +1(t 0, t 1,..., tn) - ОТ;
3) якщо t 0, t 1 і t 2 - ОТ, то N D(t 0, t 1, t 2) - ОТ;
4) якщо t 0 та t 1 - ОТ, то N ☼ (t 0, t 1) - ОТ.
Кожна програмована на N п- арна функція є значенням деякого ОТ ППА-Ar- N. Проте, як і у випадку ОТ алгебри п- арних ЧРФ, через порушення умов арності не кожен ОТ ППА-Ar- N має певне значення. Зрозуміло, що подання програмованих на N п- арних функцій операторними термами ППА-Ar- N неоднозначне.
Нехай функції a та b трактуються як предикати. Тоді функції nsg (a), a × b і a+b можна трактувати як предикати Ø a, a & b та a Ú b відповідно. Враховуючи, що a®b можна подати як Ø a Ú b, a«b можливо подати як (a®b) & (b®a), легко отримати функції, які моделюють указані предикати.
Приклад 1. Функції-константи програмовані.
Такі функції отримуються із базових функцій о, s та I за допомогою операцій S n +1.
Приклад 2. Функції пsg (x 1) та sg (x 1) програмовані.
Справді, пsg (x 1)= 
, sg (x 1)= 
(
.
Приклад 3. Функцiя | x 1- x 2| програмована.
Справдi, | x 1- x 2| = (
)+(
).
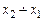Приклад 4. Предикати x 1> x 2, x 1³ x 2, x 1= x 2 та x 1¹ x 2 програмовані.
Предикат x 1> x 2 моделюється функцiєю 
. Предикат x 1³ x 2 моделюється функцiєю 
, предикат x 1= x 2 можна подати у вигляді (x 1³ x 2)&(x 2³ x 1), предикат x 1¹ x 2 - у вигляді Ø (x 1= x 2).
Приклад 5. Функція mod(x 1, x 2) програмована.
Функцію mod(x 1, x 2) можна подати операторним термом
N ☼ (S 3(
, S 2(s, I 
), I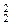 
), 
).
Приклад 6. Функцiю x 1+ x 2 можна отримати із базових функцій о, s, I , ´ 
за допомогою операцій N ☼ та S n +1.
Оскільки x 1< x 2 +x 3 Û nsg (((x 1+1) 
) 
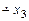)=1, предикат x 1< x 2 +x 3 моделюєтьсяфункцією nsg (((x 1+1) ) 
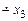), ОТ a якої має вигляд
S 3(, 13, S 3(, S 3(, S 2(s, I 
), I 
), I 
)).
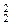Тому x 1+ x 2 можна подати OT S 4(N ☼( a, S 2(s, I )), о 2, I , I ). Отже, функцію + можна не включати до базових програмованих на Nп- арних функцiй.
Приклад 7. Аналогічно випадку V -квазіарних функцій, функцію f = N D(a, g, h) можливо подати у вигляді f=g × sg (a)+ h × nsg (a). Отже, операцiю розгалуження N D можна промоделювати, використовуючи базові функції о, s, I , ´ й операції суперпозицiї та циклу.
ЛЕКЦІЯ 6
ПЛАН
1. Поняття нумерації. Канторові нумерації пар та n -ок натуральних чисел.
2. Функція Геделя та її основна властивість.
3. Теорема про представлення операції примітивної рекурсії.
1. Поняття нумерації. Канторові нумерації пар та n -ок натуральних чисел
Різні формальні моделі алгоритмів можуть діяти на різних множинах об’єктів. Наприклад, машини Тьюрінга і нормальні алгоритми є вербальними алгоритмами, МНР-програми визначають функції натуральних аргументів та значень. Для порівняння різних формальних моделей і для переходу від одної моделі до іншої треба кодувати елементи одної множини елементами іншої множини (див. лекцію 2).
Зауважимо, що МНР-програми, машини Тьюрінга, нормальні алгоритми Маркова визначають універсальні класи алгоритмів.
З поняттям кодування тісно пов’язане поняття ефективної нумерації.
Розглянемо спочатку поняття нумерації в загальному вигляді. Нумерацiєю множини А називають сюр’єктивне функцiональне вiдображення x: N ® А.
Це означає, що кожний елемент b Î А має номер iз N (можливо, не єдиний) та кожне n Î N є номером єдиного елемента x(n)Î А.
Однозначною нумерацiєю множини А називають бієктивне вiдображення x: N → А.
У теорiї алгоритмiв особливий iнтерес викликають ефективнi нумерацiї, якi дозволяють за кожним b Î А ефективно (тобто за допомогою певного алгоритму) визначити його номер та за кожним n Î N ефективно визначити той елемент x(n)= b Î А, який нумерується цим n.
Нумерацiю x: N → А називають ефективною, якщо iснують алгоритми A і B:
- для кожного а Î А A(а)Îx-1(а);
- для кожного n Î N B(п)=x(п).
Таким чином, x: N → А - ефективна нумерація Û x-1: А → N - кодування А на N.
Розглянемо тепер нумерацiї пар та n -ок натуральних чисел. Такі нумерацiї названi канторовими. Канторовi нумерацiї є однозначними ефективними нумерацiями.
Усi пари натуральних чисел розташуємо в послiдовнiсть таким чином:
пара (x, y) йде ранiше за пару (u, v) Û x + y < u+v або (x + y = u+v та x < u).
Отже, маємо таку послідовність: (0,0); (0,1); (1,0); (0,2); (1,1); ….
Номер пари (x, y) в такiй послiдовностi позначають C (x, y) та називають канторовим номером пари (x, y). Наприклад, C (0,0)=0, C (0,2)=3.
Лiву та праву компоненти пари з номером n позначають вiдповiдно l (n) і r (n). Наприклад, l (4)=1, r (3)=2. Функцiї l (n) та r (n) називають вiдповiдно лiвою й правою координатними функцiями.
Теорема 1. Функцiї C (x, y), l (n) та r (n) - ПРФ.
Пара (x, y) знаходиться на x -му мiсцi пiсля пари (0, x + y). Перед парою (0, x + y) знаходиться x + y груп пар з однаковою сумою компонент, причому в групi із сумою компонент m мiститься m +1 пара. Тому перед парою (0, x + y) знаходиться n = 1+2+...+ (x + y) = (x + y +1) × (x + y) /2 пар. Звiдси C (x, y)= n + x, тобто C (x, y) = [(x + y +1) × (x + y) /2]+ x = [((x + y)2+3 x + y)/2]. Отже, функція C (x, y) є ПРФ.
Нехай x = l (n), y = r (n). Тоді
2 n =2 × C (x, y)=((x + y)2+3 x + y)/2, 8 n +1=(2 x +2× y +1)2+8 x = (2 x +2 y +3)2-8 y -8.
Звідси
2 x +2 y +1£ [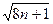 
]<2 x +2 y +3, x + y +1£ [([ 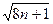]+1)/2]< x + y +2.
Отже,
x + y +1= [([ 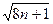]+1)/2].
Але n = C (x, y)= [(x + y +1) × (x + y)/2]+ x, звiдки функція
l (n)= x = 
[(x + y +1) × (x + y)/2] = [[([ 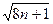]+1)/2] × [([ ] 
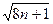)/2]/2]
є ПРФ.
Тепер функцiя r (n) = y = (x + y +1)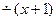 
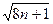= [([ ]+1)/2] 
l (n)+1) є ПРФ.
Зрозумiло, що функцiя C (x, y) задає бiєкцiю N ´ N → N, пара функцiй (l (n), r (n)) задає бiєкцiю N → N ´ N. При цьому функцiї C, l та r зв’язaнi такими тотожностями:
C (l (n), r (n))= n; l (C (x, y))= x; r (C (x, y))= y. (*)
Зауважимо, що якщо функцiї С, L, R зв’язанi тотожностями
C (L (n), R (n))= n; L (C (x, y))= x; R (C (x,y))= y, (**)
то, називаючи C (x, y) номером пари (x, y), дiстанемо однозначну нумерацiю N ´ N.
З іншого боку, нехай задана однозначна нумерацiя N ´ N, тобто всi пари натуральних чисел без повторiв розташованi в послiдовнiсть (x 0, y 0), (x 1, y 2),..., (xn, yn),.... Поклавши тепер L (n)= xn, R (n)= yn та C (xn, yn)= n, дiстанемо функцiї, зв’язанi тотожностями (**).
Маючи нумерацiю пар натуральних чисел, можна ввести нумерацiю n -ок натуральних чисел для довiльного n:
C 3(x 1, x 2, x 3)= C (C (x 1, x 2), x 3);
Ck +1(x 1, x 2,..., xk+ 1) = Ck (C (x 1, x 2), x 3,..., xk+ 1) = C (... С (C (x 1, x 2), x 3),...), xk+ 1)
для k> 2.
Якщо Cп (x 1, x 2,..., xп)= m, то координатнi функцiї Cn 1,..., Cnn вводимо так:
Cn 1(m)= x 1; Cn 2(m)= x 2;..., Cnn (m)= xn.
Для функцiй Cп, Cn 1,..., Cnn маємо такi тотожностi:
Cп (Cn 1(x),..., Cnn (x))= x;
Cnk (Cп (x 1, x 2,..., xп))= xk, 1£ k £ n.
Теорема 2. Функцiї Cп, Cn 1,..., Cnn є ПРФ.
Справдi, маємо
Cnn (m)= xn = r (m); C nn -1(m)= xn- 1= r (l (m));..., Cn 2(m)= x 2= r (l (... l (m))…); Cn 1(m)= x 1= l (l (... l (m))..).
Задамо однозначну ефективну нумерацiю всiх скiнченних послiдовностей натуральних чисел на основі канторових нумераційних функцій. Спочатку задамо кодування k таких послідовностей:
k(Æ)=0;
k(а 1,..., ап) = C (Cп (а 1,..., ап), п -1)+1.
Таке відображення k: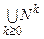 
→ N бієктивне. Тепер обернене відображення η=k-1 - шукана однозначна нумерацiя.
Однозначну ефективну нумерацiю всiх скiнченних послiдовностей натуральних чисел можна також задати на основі наступного кодування s скiнченних послiдовностей:
s(Æ)=0;
s(а 1,..., ап)=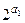 
+ 
+...+ 
.
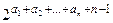Бiєктивнiсть вiдображення s: 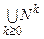→ N випливає з однозначностi подання кожного натурального числа в двiйковiй системi числення. Обернене відображення l=s-1 - шукана однозначна нумерацiя.
Аналогічно задаємо однозначну ефективну нумерацiю всiх непорожніх скiнченних послiдовностей натуральних чисел. Модифікуючи кодування s, дістаємо однозначне кодування
n: 
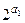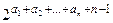→ N: n(а 1,..., ап)= + +...+ -1.
Обернене відображення z=n-1 - шукана однозначна нумерацiя.
Поиск по сайту: