Геделеві нумерації ЧРФ

Поняття геделевої нумерації для випадку нумерацій n -арних ЧРФ уточнимо таким чином.

Нумерація x геделева, якщо існують рекурсивні функції f і g, такі:

- для кожного т Î N j = x _{f ( m )};

- для кожного k Î N x _k = j .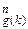

Це означає, що існує пара алгоритмів, перший із яких за стандартним індексом функції знаходить її x-індекс, а другий за x-індексом функції знаходить її стандартний індекс.

Твердження 2. Кожна геделева нумерація ефективна.

Справді, нехай нумерація x геделева. Тоді за ЧРФ, заданою стандартним індексом (кодом МНР-програми) т як j , ефективно (використовуючи РФ f) знаходимо її x-індекс f (m); за x-індексом k ефективно (використовуючи РФ g) знаходимо ЧРФ, задану кодом МНР-програми (стандартним індексом) g (m).

Нехай F - деякий клас функцій вигляду Х→Y, для якого задана нумерація x: N→ F. Із такою нумерацією x зв’язана функція и: N × Х→Y, що визначається умовою и (п, х) = x _п (х). Зазначену функцію и називають спряженою з нумерацією x.

Нумерація називається обчислюваною, якщо спряжена з нею функція є ЧРФ.

Твердження 3. Кожна геделева нумерація обчислювана.

Нехай нумерація x геделева, нехай g - РФ із визначення геделевої нумерації. Тоді спряжена до нумерації x функція и (п, х) = x _п (х) = j 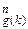є ЧРФ за тезою Чорча.

Зворотне твердження, взагалі кажучи, неправильне. Кожна обчислювана нумерація в певному смислі зводиться до геделевої, в той же час існують приклади негеделевих обчислюваних нумерацій. Проте такі приклади досить неприродні, вони використовують дуже штучні конструкції.

ЛЕКЦІЯ 9

ПЛАН

1. Поняття універсальної функції. Теорема про універсальні функції. Існування універсальної ЧРФ.

2. S-M-N-теорема, приклади її використання.

1. Поняття універсальної функції. Теорема про універсальні функції. Існування універсальної ЧРФ

Функцiя и (y, x ₁ ,..., x_п) називається унiверсальною функцiєю для класу F ^п функцій із F фіксованої арності п, якщо:

- для кожного значення m функцiя и (y, x ₁ ,..., x_п)Î F ^п;

- для кожної f Î F ^п iснує таке m, що f (x ₁ ,..., x_n)= и (т, x ₁ ,..., x_п) для всiх значень x ₁ ,..., x_п .

Теорема 1. Нехай T - деякий клас тотальних п-арних функцiй на N, який мiстить функцiї о, s, I та замкнений вiдносно суперпозицiї. Нехай функцiя u унiверсальна для T ^п. Тодi u Ï T.

Припустимо супротивне: така u Î T, тобто u Î T ^{п +1}. Визначимо функцiю g таким чином: g (x ₁, ..., x_n)= и (x ₁, x ₁, ..., x_п)+1. Тодi g Î T ^п. У силу унiверсальностi функцiї u iснує таке m, що g (x ₁, ..., x_n)= и (т, x ₁, ..., x_п) для всiх значень x ₁ ,..., x_п . Звiдси g (т, x ₂, ..., x_n) = = и (т, т, x ₂, ..., x_п). Але за визначенням функцiї g g (т, x ₂, ..., x_n) = и (т, т, x ₂, ..., x_п)+1. Дiстали суперечнiсть, бо функцiї g та u тотальнi.

Наслiдок 1. Функцiя, унiверсальна для класу n-арних РФ, не є ЧРФ.

Справдi, така функцiя тотальна i не є РФ.

Наслiдок 2. Функцiя, унiверсальна для класу n-арних ПРФ, не є ПРФ.

Теорема 2. Існує РФ, унiверсальна для класу n-арних ПРФ.

На основi розглянутої вище ефективної нумерацiї ПРФ задамо алгоритм для обчислення функцiї и (у, x ₁, ..., x_п), унiверсальної для класу n -арних ПРФ. За п як кодом ОТ алгебри ПРФ побудуємо вiдповiдний ОТ i перевiримо, чи задає вiн n -арну ПРФ. Якщо нi, то видаємо значення 0 (тобто и (у, x ₁, ..., x_п) – суть функцiя о ^п ). Якщо так, то обчислимо значення заданої цим термом функцiї над x ₁, ..., x_п. Отже, функцiя и - тотальна АОФ, тому за тезою Чорча вона рекурсивна.

Наслiдок 1. Існує РФ, яка не є ПРФ.

Наслiдок 2. Для вiдповiдних класiв функцiй маємо строгi включення ПРФÌРФÌЧРФ.

Теорема 3. Існує ЧРФ, унiверсальна для класу n-арних ЧРФ.

Розглянемо функцiю и (у, x ₁, ..., x_п) = j 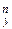(x ₁, ..., x_п). Вона є унiверсальною для класу n -арних ЧРФ. Справді, для кожного m функцiя и (т, x ₁, ..., x_п)=j (x ₁, ..., x_п) - ЧРФ. З іншого боку, кожна n -арна ЧРФ f - суть функцiя j для деякого m, тобто f (x ₁, ..., x_п) =j (x ₁, ..., x_п) = и (т, x ₁, ..., x_п) для всiх x ₁, ..., x_п.

Задамо алгоритм для обчислення функцiї u. За y як за кодом МНР-програми вiдновимо програму P_y для функцiї j 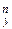. Потiм запустимо P_y над значеннями x ₁, ..., x_п. Отримане значення є значенням j 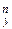(x ₁, ..., x_п). За тезою Чорча u - n -арна ЧРФ.

МНР-програма, яка обчислює унiверсальну ЧРФ, називається унiверсальною МНР - програмою. Унiверсальнiсть зовсiм не означає, що така програма мiстить у собi всi програми для обчислення n -арних ЧРФ! Унiверсальна програма вмiє декодувати довiльне число y в програму P_y, а далi вона моделює роботу P_y. Тому така унiверсальна програма може бути задана в явному виглядi. Отже, можна конструктивно знайти iндекс k унiверсальної функцiї u в стандартній нумерацiї (n +1)-арних ЧРФ, тобто u – суть функцiя j .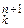

Машина Тьюрiнга, яка обчислює унiверсальну ЧРФ, називається унiверсальною МТ. Таку МТ, здатну моделювати роботу довiльної МТ за її кодом, теж можна задати в явному виглядi.

Унiверсальна МНР-програма та унiверсальна МТ є абстрактними моделями сучасних комп’ютерiв. Вони реалiзують в абстрактному виглядi принцип програмного керування: виконання заданої програми над заданими даними.

Поиск по сайту: