Примеры решения задач по физике — концентрические проводящие сферы

Для расчета различных систем автоматического управления их обычно разбивают на отдельные элементы, динамическими характеристиками которых являются дифференциальные уравне­ния не выше второго порядка. Причем различные по своей физиче­ской природе элементы могут описываться одинаковыми диффе­ренциальными уравнениями, поэтому их относят к определенным классам, называемым типовыми звеньями.

Изображение системы в виде совокупности типовых звеньев с указанием связей между ними называется структурной схемой. Она может быть получена на основе как дифференциальных урав­нений, так и передаточных функций. Данный способ и составляет суть структурного метода, т. е. метода представления систем ав­томатического управления различной физической природы.

Хотя структурный метод не предлагает новых способов расчета, он позволяет наглядно представить взаимосвязь элементов систе­мы и оценить при наличии соответствующего опыта отдельные свойства переходных и статических процессов. Он настолько ши­роко используется в практике проектирования, что, по существу, может считаться одним из «языков», на котором обсуждаются свойства систем автоматического управления.

Рассмотрим подробнее отдельные типовые звенья и их различ­ные динамические характеристики.

3.1. ТИПОВЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ

3.1.1. Пропорциональное (усилительное) звено

Пропорциональным называется звено, поведение которого опи­сывает алгебраическое уравнение

y =ku,

где k - коэффициент усиления. Строго говоря, это звено не являет­ся динамическим, но относится к типовым.

Примерами таких звеньев могут служить безынерционные усилители. механические редукторы, многие датчики сигналов и т. д. передаточная функция звена следующая:

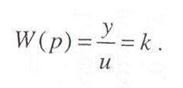
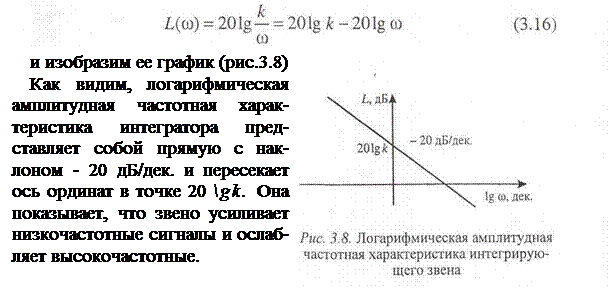
Переходная характеристика (реакция звена на скачкообразное входное воздействие 1(t)) имеет вид

Импульсная переходная функция пропорционального звена оп­ределяется выражением

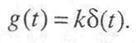
Модальные характеристики (собственные значения и собствен­ные векторы) для него отсутствуют.

Заменив в передаточной функции р на jω, получим выражения
для частотных характеристик. Амплитудно-фазовая характеристика представляет собой точку на комплексной плоскости в соответствии с формулой

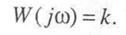
Вещественная частотная характеристика определяется соотношением (рис. 3.1)

а мнимая частотная характеристи­ка отсутствует (I(ω)=0).

Амплитудная частотная характеристика может быть построена по соотношению

и имеет тот же вид, что и ВЧХ. Выражение для ФЧХ следующее:

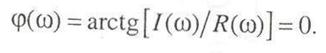
Таким образом, при прохождении через пропорциональное звено амплитуда периодического входного сигнала изменяется в k раз, а базовый сдвиг отсутствует.

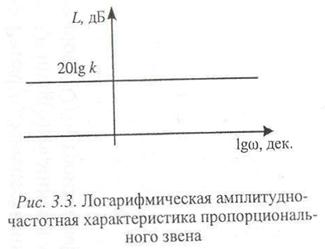Амплитудно-фазовая характеристика звена имеет вид точки на комплексной плоскости (рис. 3.2).

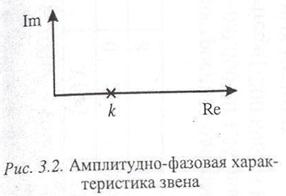
Логарифмическая АЧХ звена представляет собой прямую, па­раллельную оси абсцисс:

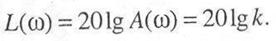
Как следует из выражений (3.3, 3.4) и рис. 3.3, пропорциональ­ное звено пропускает входные сигналы без искажений.

3.1.2. Дифференцирующее звено

Дифференцирующим называется звено, которое описывается дифференциальным уравнением

y =ku.

Его передаточная функция имеет вид

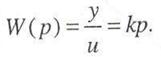
Примером дифференцирующего звена часто может служить тахогенератор постоянного тока. Переходная характеристика диффе­ренцирующего звена определяется выражением

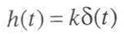
и имеет вид 5 -функции (рис. 3.4).

Импульсная переходная функция (рис. 3.5) представляет собой «дуплет» δ –функций

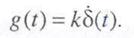
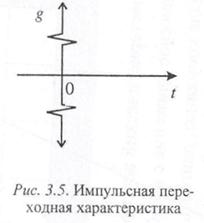
Рассмотрим теперь частотные характеристики звена. Ампли­тудно-фазовая характеристика

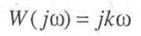
совпадает с положительной мнимой полуосью комплексной плос­кости; вещественная частотная характеристика равна нулю, Л(ц>) = 0; мнимая частотная характеристика соответствует выра­жжению

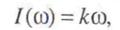
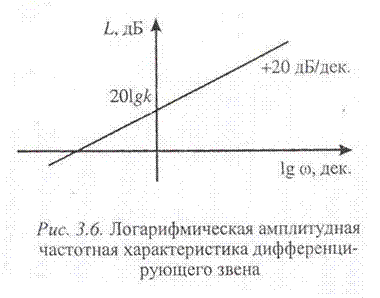
т. е. представляет собой линейно нарастающую функцию. С ней совпадает амплитудная частотная характеристика, которая имеет вид

Фазовую частотную характеристику можно определить по со­отношению

Следовательно, на всех частотах имеется постоянный фазовый сдвиг.

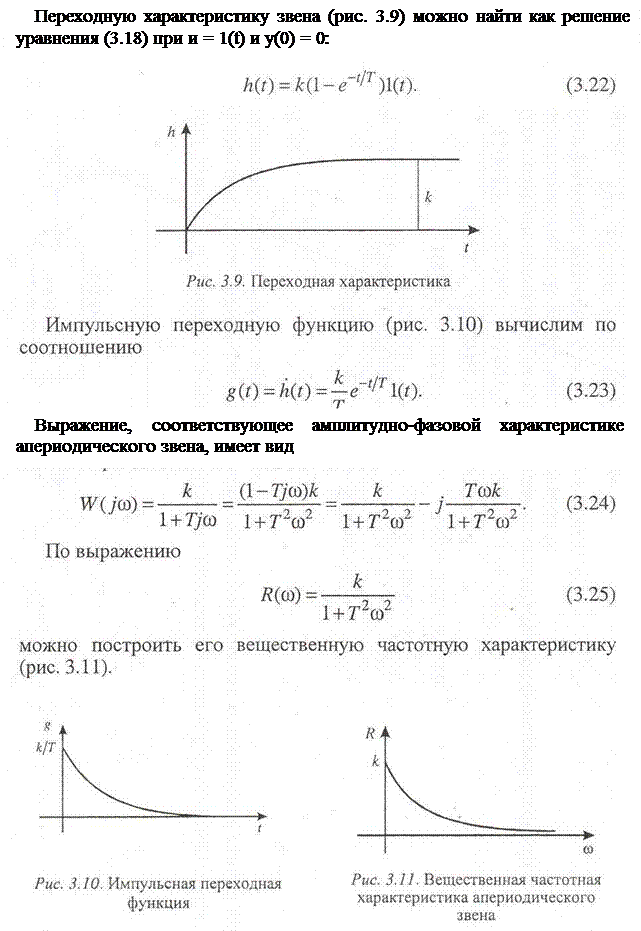
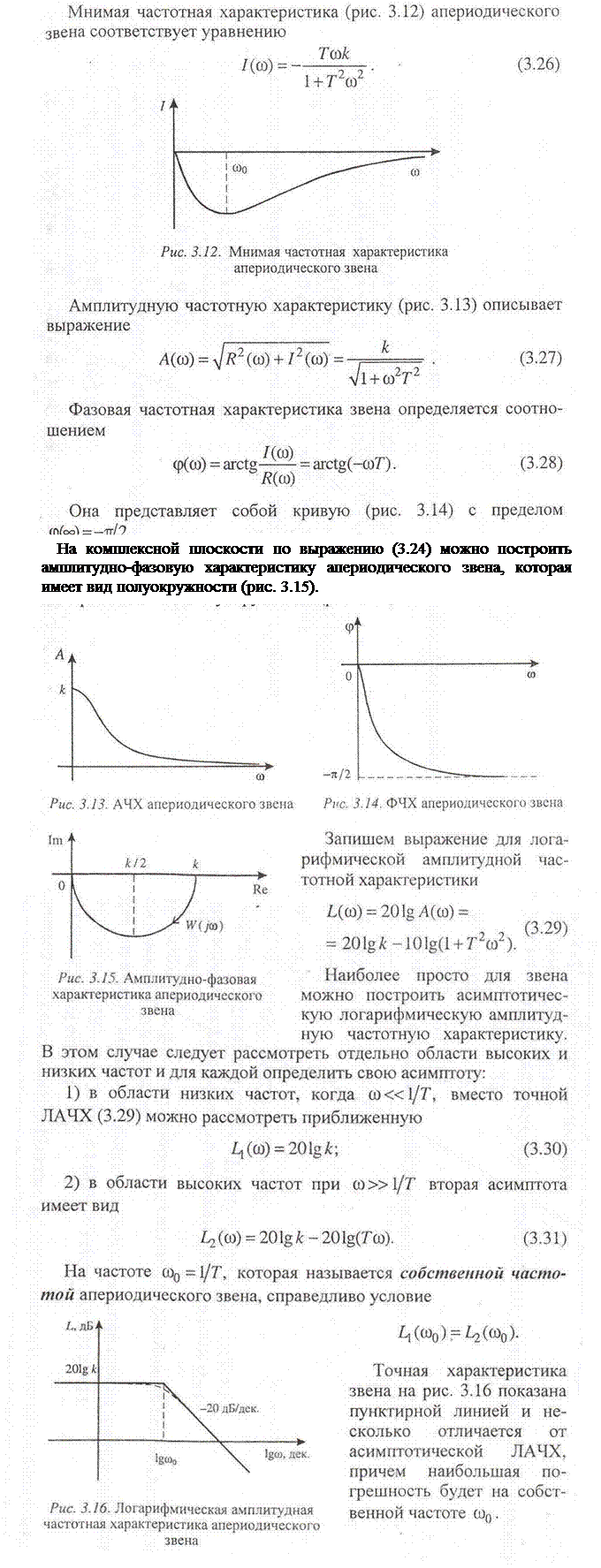
Причем се можно получить, исследуя отдельно области низких _и высоких частот или суммируя ЛАЧХ пропорционального и дифференцирующего звеньев.

Нетрудно убедиться, сравнивая выражения (3.28) и (3.29) с выражениями (3.37) и (3.38), в том, что логарифмические ампли­тудная и фазовая частотные характеристики форсирующего звена представляют собой зеркальное отображение относительно оси абсцисс соответствующих логарифмических характеристик апе­риодического звена.

		Для определения модальных характеристик запишем характери­стическое уравнение звена

Примеры решения задач по физике — концентрические проводящие сферы

Автор Sergey Seliverstov

Суббота, Февраль 25, 2012

Среди школьных задач по физике особняком стоят те, которые связаны с концентрическими проводящими сферами. Эти сферы могут быть заряжены, заземлены, могут находиться в поле внешних зарядов, вариаций много. Думаю можно сказать, что это один из самых сложных типов задач, входящих в школьный курс физики. Я и сам в свое время сломал не мало копий, пытаясь разобраться в том, как они решаются, со своим преподавателем. Не в последнюю очередь, конечно, непонимание этого материала связано с неспособностью большинства школьных учителей его доступно объяснить. Если эта проблема касается и вас, предлагаю вашему вниманию сей опус. Возможно, ознакомившись с ним, что-нибудь для вас прояснится.

Тексты заданий я взял из сборника задач по физике для подготовительных отделений вузов.

Задача 1. Сфера радиуса r, которой сообщен заряд q, окружена концентрической тонкостенной проводящей сферической оболочкой радиуса R, заряд которой равен Q. Определите потенциалы сфер φ _in(внутренней) и φ _ex (внешней).

Решение. Потенциал на поверхности внутренней сферы φ _ex складывается из двух потенциалов: внешней сферы φ ₁ и собственно внутренней сферы φ ₂.

Потенциал внешней сферы φ ₁ в каждой точке ее внутреннего объема одинаков и равен потенциалу на ее поверхности (подробнее о решении задач на тему «Потенциал» читайте в этой статье):

Потенциал внутренней сферы φ ₂ определяется известным соотношением:

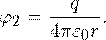
Тогда общий потенциал φ _in на поверхности внутренней сферы равен:

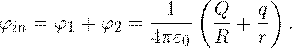
Потенциал на поверхности внешней сферы также складывается из двух потенциалов: внутренней сферы φ’ ₁ и собственно внешней сферы φ’ ₂.

Потенциал внутренней сферы φ’ ₁ на расстоянии R от ее центра определяется известным соотношением:

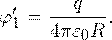
Формула, определяющая потенциал внешней сферы φ’ ₂ на ее поверхности, также хорошо известна:

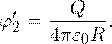
Тогда общий потенциал на поверхности внешней сферы равен:

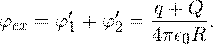
Задача 2. Металлический шар радиуса R ₁, заряженный до потенциала φ, окружают тонкой сферической проводящей оболочкой радиуса R ₂. Определите потенциал шара φ ₁ после того, как он будет соединен проводником с оболочкой. Первоначальный заряд оболочки равен нулю, центры оболочки и шара совпадают.

Решение. До соединения сфер проводником заряд первой был равен:

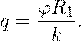
После соединения часть заряда с внутренней сферы перетекло на внешнюю. Ток прекратился в тот момент, когда потенциал шара стал равен потенциалу внешней оболочки. Удобнее поэтому искать не потенциал шара, а равный ему потенциал внешней оболочки. В соответствии с результатами, полученными в предыдущей задаче, этот потенциал определяется выражением:

где q ₁ и q ₂ — заряды шара и внешней оболочки после соединения их проводником соответственно. По закону сохранения заряда q = q ₁ + q ₂. После несложных преобразований получаем:

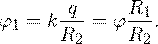
Задача 3. Металлический шар радиуса R ₁, заряженный до потенциала φ, окружают концентрической сферической проводящей оболочкой радиуса R ₂. Чему станет равен потенциал шара φ ‘, если заземлить оболочку?

После заземления проводящей оболочки весь положительный заряд, образовавшийся на ней вследствие явления электростатической индукции, стекает на землю. На ней остается только отрицательный заряд, поскольку он притягивается к положительному заряду внутренней сферы

Решение. Зная потенциал шара в начальный момент времени и его радиус, можно найти заряд на нем:

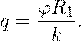
Вследствие явления электростатической индукции на внешней оболочке должно произойти разделение заряда. Отрицательный заряд перетечет на внутреннюю поверхность оболочки, положительный — на внешнюю (см. рисунок). Это же явление возникало и в предыдущих задачах, но мы не принимали его во внимание. Почему? В условии задач было указано, что оболочка тонкая, и такое «разбегание» зарядов не приводило к сколько-нибудь существенному изменению конфигурации электростатического поля.

В этой задаче учет данного явления важен, поскольку оболочку заземляют. После заземления положительный заряд с оболочки стечет на землю, останется лишь отрицательный q ₂, поскольку он притягивается к положительному заряду q ₁ внутренней сферы. Потенциал заземленной оболочки станет равен потенциалу земли, то есть нулю. В этой связи и в соответствии с результатом, полученным при решении первой задачи, получаем равенство:

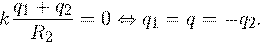
Используя выражение для расчета потенциала внутренней сферы подобной системы, полученное в первой задаче, находим окончательно требуемый потенциал шара:

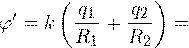
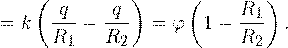
Опыт показывает, что редко кто понимает решение этих задач во всех деталях с первого раза. Обычно приходится долго и настойчиво разъяснять ученикам все те мелочи, без осознания которых решение сводится к пустым преобразованиям буквенных выражений с целью получения приведенного в конце учебника ответа. Понять физическую сущность этих задач и научиться применять полученные знания в будущем не просто. Однако в этом и состоит основная методическая ценность данной темы в школьном курсе физики. Лучшим помощником в ее изучении непременно станет профессиональный репетитор, грамотный наставник, который сможет придумать понятное именно вам объяснение и ответит на все возникшие вопросы. Кстати, если таковые имеются, вы можете задать их ниже в комментариях.

Репетитор по физике и математике
Сергей Селиверстов

Учителя только открывают двери, дальше вы идете сами.
© Китайская пословица

Поделиться…

Метки: задачи по физике
Опубликовано в категории Методическая копилка | Комментарии (6)»

Поиск по сайту: