АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Pressure/velocity variation

Читайте также:
  1. AC MOTORS
  2. ACCURACY, RELIABILITY AND VALIDITY
  3. Correlation of style, norm and function in the language
  4. Electrical measurement. Electrical measuring instruments and their classification.
  5. ELEMENTS OF MECHANICS OF LIQUIDS.
  6. Essential concepts of decoding stylistic analysis and types of foregrounding
  7. Familiar colloquial style.
  8. Hyperbole
  9. II. Prepositions and Conjunctions.
  10. Legal systems of the world
  11. Main historical sources of the Modern English spelling.
  12. Measurement of AC frequency and phase angle. Design and function of frequency and phase meters.

Consider the steady, flow of a constant density fluid in a converging duct, without losses due to friction (figure 1). The flow therefore satisfies all the restrictions governing the use of Bernoulli's equation. Upstream and downstream of the contraction we make the one-dimensional assumption that the velocity is constant over the inlet and outlet areas and parallel.

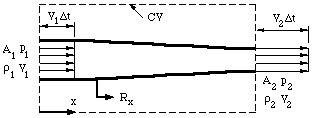
  Figure 1. One-dimensional duct showing control volume.


When streamlines are parallel the pressure is constant across them, except for hydrostatic head differences (if the pressure was higher in the middle of the duct, for example, we would expect the streamlines to diverge, and vice versa). If we ignore gravity, then the pressures over the inlet and outlet areas are constant. Along a streamline on the centerline, the Bernoulli equation and the one-dimensional continuity equation give, respectively,

 

 


1 | 2 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)