 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Кинематика
|
Читайте также: |
ЛЕКЦИЯ 5
Кинематикой называется раздел механики, в котором изучается движение материальных точек и тел в пространстве с геометрической точки зрения, вне связи с силами, определяющими это движение.
Мы будем изучать простейшую форму движения – механическое движение, то есть происходящее во времени изменение положения одного тела относительно другого, с которым связана система координат, называемая системой отсчета.
Эта система может быть как движущейся, так и условно неподвижной.
Рассматривая движение, мы связываем изменение положения тела или точки с течением времени.
При изучении движения всегда устанавливаем начало отсчета времени  .
.
Непрерывную кривую, которую описывает точка при своем движении, называют траекторией.
Если траектория – прямая линия, то движение называется прямолинейным, если кривая – криволинейным.
Способы задания движения.
Задать движение точки по отношению к избранной системе отсчета – это значит указать способ, при помощи которого можно определить положение точки в любой момент времени. Существуют три способа задания движения:
1. Векторный способ
Положение точки в пространстве однозначно определяется заданием радиуса-вектора  , проведенного из некоторого неподвижного центра 0 в данную точку М.
, проведенного из некоторого неподвижного центра 0 в данную точку М.
Для определения движения точки нужно знать, как изменяется с течением времени  , то есть должна быть известна функция
, то есть должна быть известна функция
 (1)
(1)

Годографом какого-либо вектора называют кривую, которую вычерчивает конец этого вектора при изменении его аргумента (предполагается, что начало вектора находится в одной и той же точке).
Таким образом, годографом радиуса-вектора является траектория точки.
2. Координатный способ
Положение точки М в системе отсчета ОХУ определяется декартовыми координатами  .
.
При движении точки М ее координаты изменяются с течением времени. Следовательно, координаты  движущейся точки, являются функциями времени.
движущейся точки, являются функциями времени.
 (2)
(2)

Эти уравнения называются уравнениями движения точки в декартовых координатах.
Пусть движение точки М в плоскости задано уравнениями

Из первого уравнения выразим время  и подставим во второе:
и подставим во второе:  – уравнение траектории точки.
– уравнение траектории точки.
3. Естественный способ задания движения.
Этот способ применяется в том случае, если траектория точки заранее известна. Выберем на траектории неподвижную точку 0, которую назовём началом отсчёта дуговой координаты.
Положение точки М на траектории будем определять дуговой координатой  , отложенной на траектории от начала отсчета 0. Расстояния, отложенные в одну сторону от точки 0, будем считать положительными, в другую – отрицательными, то есть установим направление отсчета дуговой координаты.
, отложенной на траектории от начала отсчета 0. Расстояния, отложенные в одну сторону от точки 0, будем считать положительными, в другую – отрицательными, то есть установим направление отсчета дуговой координаты.
При движении точки М расстояние  от этой точки до неподвижной точки 0 изменяется с течением времени:
от этой точки до неподвижной точки 0 изменяется с течением времени:
 (3)
(3)
– уравнение движения точки М.
Скорость точки
1. При векторном способе задания движения
Пусть в момент времени  положение точки М определяется
положение точки М определяется  , а в момент
, а в момент  –
–  .
.
Вектор 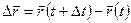 будем называть вектором перемещения точки за время
будем называть вектором перемещения точки за время  . Отношение
. Отношение  к
к  называется средней скоростью за промежуток времени
называется средней скоростью за промежуток времени  .
.  (4)
(4)
Скоростью точки в данный момент времени называется предел отношения вектора перемещения точки к промежутку времени, за которое при стремлении этого промежутка времени к нулю.
 (5)
(5)
Скорость точки – это вектор, направленный по касательной к траектории в сторону движения.
2. При координатном способе задания движения.
Пусть движение точки задано координатным способом

Тогда для радиуса-вектора точки М можно записать
 (*)
(*)
где  – единичные орты осей
– единичные орты осей  соответственно.
соответственно.
Согласно (5)  дифференцируем (*)
дифференцируем (*)
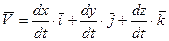 (**)
(**)
Для вектора  справедливо соотношение:
справедливо соотношение:
 (***)
(***)
где  – проекции
– проекции 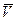 на оси
на оси  .
.
Сравнивая (**) и (***), получим
 (6)
(6)
Модуль скорости точки
 (7)
(7)
Направление скорости определяется направляющими косинусами:

3. При естественном способе задания движения
Пусть в момент времени  положение точки М определяется координатой
положение точки М определяется координатой  , в момент
, в момент  –
–  .
.
Согласно (5)
 (*)
(*)
Вычислим модуль и определим направление  :
:

Вектор  направлен так же, как
направлен так же, как  . При
. При  направление этого вектора стремится к направлению касательной к траектории в точке М. Обозначим единичный орт касательной через
направление этого вектора стремится к направлению касательной к траектории в точке М. Обозначим единичный орт касательной через  .
.

Таким образом  , следовательно
, следовательно  , так как
, так как  .
.
И равенство (*) принимает вид:
 (8)
(8)
Модуль  , направление
, направление  совпадает с
совпадает с  .
.
ЛЕКЦИЯ 6
Ускорение точки.
1. При векторном способе задания движения
Предположим, что в момент времени  скорость, точки –
скорость, точки –  , а в момент
, а в момент  –
–  .
.
Предел приращения скорости к приращению времени  , за которое произошло это приращение, при условии, что
, за которое произошло это приращение, при условии, что  , называется ускорением точки в данный момент времени
, называется ускорением точки в данный момент времени
 (9)
(9)
Годографом скорости называется кривая, которую вычерчивает конец вектора скорости при движении точки, если вектор скорости проводится из одной и той же точки.
2. При: координатном способе задания движения
Вектор скорости точки

С учетом.(9)
 (*)
(*)
На для вектора ускорения точки имеем
 (**)
(**)
Сравнивая (*) и (**), получим

Модуль ускорения точки

Направление вектора ускорения определяется направляющими косинусами

3. При естественном способе задания движения
Пусть известна траектория точки. Возьмем две близкие на траектории точки М и М1  . Проведем касательные к траектории в точках М и М1 –
. Проведем касательные к траектории в точках М и М1 –  и
и  .
.

Вектор  перенесем в точку М параллельно ему самому и проведем плоскость через
перенесем в точку М параллельно ему самому и проведем плоскость через  и
и  . Эта плоскость называется соприкасающейся плоскостью.
. Эта плоскость называется соприкасающейся плоскостью.
Плоскость, перпендикулярная ( ) касательной, называется нормальной плоскостью.
) касательной, называется нормальной плоскостью.
Плоскость  нормальной и соприкасающейся плоскостям называется спрямляющей плоскостью.
нормальной и соприкасающейся плоскостям называется спрямляющей плоскостью.

Три взаимно перпендикулярных плоскости: нормальная, соприкасающаяся, спрямляющая образуют естественный трехгранник.
Линия пересечения нормальной и соприкасающейся плоскостей называется главной нормалью. Орт главной нормали –  .
.
Линия пересечения нормальной и спрямляющей плоскостей называется бинормалью траектории. Орт бинормали –  .
.
Три взаимно перпендикулярные оси: касательная, направленная в сторону возрастания дуговой координаты, главная нормаль, направленная в сторону вогнутости траектории, бинормаль, направленная по отношению к  и
и  так же, как ось
так же, как ось  по отношению к осям
по отношению к осям  , называются естественными осями.
, называются естественными осями.
Угол между касательными в двух ближайших точках траектории называется углом смежности,  .
.

Кривизной кривой в точке М называется предел отношения угла смежности к абсолютному значению длины дуги ММ1 между ближайшими точками траектории 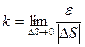 .
.
Радиусом кривизны кривой в точке М называется величина обратная кривизне: 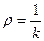 .
.
Получим формулу для вычисления ускорения точки М  .
.
Продифференцируем по времени обе части этого равенства
 (*)
(*)
Вычислим  .
.

 направлен параллельно вектору
направлен параллельно вектору  , то есть в сторону вогнутости траектории и лежит в плоскости, проходящей через точку М и векторы
, то есть в сторону вогнутости траектории и лежит в плоскости, проходящей через точку М и векторы  . Таким образом,
. Таким образом,  лежит в соприкасающейся плоскости, так как при
лежит в соприкасающейся плоскости, так как при  плоскость
плоскость  МАВ совпадает с соприкасающейся плоскостью. Дифференцируем обе части. тождества:
МАВ совпадает с соприкасающейся плоскостью. Дифференцируем обе части. тождества:  ;
;  , то есть
, то есть  .
.
Следовательно,  направлен по главной нормали траектории.
направлен по главной нормали траектории.
Определим  .
.  МАВ – равнобедренный.
МАВ – равнобедренный.

Так как вектор  равен
равен  , а направлен по главной нормали, то
, а направлен по главной нормали, то 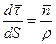 .Подставил в (*).
.Подставил в (*).
 (**)
(**)
Ускорение точки равно геометрической сумме двух векторов: один, направленный по главной нормали, называется нормальным ускорением –  , другой, направленный по касательной, называется касательным ускорением –
, другой, направленный по касательной, называется касательным ускорением –  . То есть
. То есть 
где  ,
,  ,
,  ,
,  .
.

Некоторые частные случаи движения точки
1. Прямолинейное движение.

Так как при прямолинейном движении скорость изменяется только численно, то делаем вывод, что касательное ускорение характеризует изменение скорости по численной величине.
2. Равномерное криволинейное движение
Равномерным называется такое криволинейное движение, в котором численная величина скорости остается все время постоянной:
 ,
,  ,
,  .
.
Так как ускорение при равномерном движении появляется в результате изменения направления скорости, то нормальное ускорение характеризует изменение скорости по направлению  ,
,  , проинтегрируем
, проинтегрируем  ,
, 
 – закон равномерного криволинейного движения.
– закон равномерного криволинейного движения.
3. Равномерное прямолинейное движение
 ,
,  . Следовательно,
. Следовательно,  .
.
4. Равнопеременное криволинейное движение
Равнопеременным называется такое криволинейное движение, при котором касательное ускорение остается величиной постоянной:  ,
,  ,
,  , проинтегрируем
, проинтегрируем  ,
,  ,
,  , но
, но  ,
,  .
.
Проинтегрируем 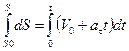 ,
,  .
.
 – закон равнопеременного криволинейного движения.
– закон равнопеременного криволинейного движения.
ЛЕКЦИЯ 7
Простейшие движения твёрдого тела.
1. Поступательное движение тела
Поступательным называется такое движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается, оставаясь параллельной самой себе.
Теорема
При поступательном движении твердого тела все точки тела описывают – одинаковые (при наложении совпадающие) траектории и имеют в каждый момент времени: одинаковые по модулю и направлению скорости и ускорения.
Доказательство:
Возьмем две произвольные точки А и В, положения которых определяются радиусами-векторами  и
и  .
.

 (*)
(*)
 , так как тело абсолютно твердое, то есть траектория точки В получается из траектории точки А параллельным смещением всех точек на постоянный вектор АВ. Таким образом„траектории точек А и В одинаковы. Продифференцируем по времени равенство (*):
, так как тело абсолютно твердое, то есть траектория точки В получается из траектории точки А параллельным смещением всех точек на постоянный вектор АВ. Таким образом„траектории точек А и В одинаковы. Продифференцируем по времени равенство (*): 
 . Продифференцируем
. Продифференцируем  , то есть
, то есть  ч.т.д.
ч.т.д.
При поступательном движении общую для всех точек тела скорость называют скоростью поступательного движения. Закон поступательного движения имеет вид:

2. Вращательное движение твердого тела
Вращательным называется такое движение твердого тела, при котором остаются неподвижными все его точки, лежащие на некоторой прямой, называемой осью вращения.
При этом движении все остальные точки тела движутся в плоскостях  оси вращения и описывают окружности, центры которых лежат на этой оси.
оси вращения и описывают окружности, центры которых лежат на этой оси.
Для осуществления этого движения следует неподвижно закрепить две произвольные точки тела А и В.
Тогда прямая АВ будет осью вращения тела и все точки, лежащие на этой прямой, во все время движения будут оставаться неподвижными.

Определим положение вращающегося тела следующим образом: зададимся направлением оси вращения  . Проведем через эту ось две полуплоскости: неподвижную Р и подвижную Q, связанную с твердым телом и вращающуюся вместе с ним. Двухгранный угол
. Проведем через эту ось две полуплоскости: неподвижную Р и подвижную Q, связанную с твердым телом и вращающуюся вместе с ним. Двухгранный угол  между этими полуплоскостями, отсчитываемый от неподвижной полуплоскости Р к подвижной Q, называется углом поворота тела. Угол поворота будем считать положительным, если, смотря навстречу оси вращения, можно увидеть его отложенным против движения часовой стрелки.
между этими полуплоскостями, отсчитываемый от неподвижной полуплоскости Р к подвижной Q, называется углом поворота тела. Угол поворота будем считать положительным, если, смотря навстречу оси вращения, можно увидеть его отложенным против движения часовой стрелки.
Численное значение угла поворота выражается в радианах:  . Угол поворота часто выражают числом оборотов N. Тогда угол
. Угол поворота часто выражают числом оборотов N. Тогда угол  в радианах, соответствующий N оборотам, определяется:
в радианах, соответствующий N оборотам, определяется:  .
.
Угол  , определяя положение подвижной полуплоскости, определяет так же положение всего вращающегося тела. Поэтому его можно рассматривать как угловую координату тела. При вращении тела
, определяя положение подвижной полуплоскости, определяет так же положение всего вращающегося тела. Поэтому его можно рассматривать как угловую координату тела. При вращении тела  изменяется от времени:
изменяется от времени:  – уравнение вращательного движения твердого тела.
– уравнение вращательного движения твердого тела.
Главными кинематическими характеристиками вращательного движения твердого тела в целом являются угловая скорость –  и угловое ускорение –
и угловое ускорение –  .
.
Пусть в момент времени  движение подвижной полуплоскости определяется углом
движение подвижной полуплоскости определяется углом  , а в момент
, а в момент  – углом
– углом  .
.
Предел отношения приращения угла к приращению времени при стремлении последнего к нулю, называется угловой скоростью тела в данный момент времени:
 .
.
Размерность  – радиан, деленный на секунду:
– радиан, деленный на секунду: 
В технике часто при равномерном вращении тела пользуются числом оборотов в минуту –  .
.
Зависимость между  и
и  имеет вид:
имеет вид:
 .
.
Величина, характеризующая быстроту изменения угловой скорости с течением времени, называется угловым ускорением
 ,
, 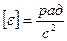 .
.
Весьма полезным является введение в рассмотрение вектора угловой скорости и углового ускорения.
Вектором угловой скорости будем называть вектор, модуль которого равен абсолютному значению производной угла поворота тела по времени, направленный вдоль оси вращения в ту сторону, откуда вращение тела видно происходящим против хода часовой стрелки  ,
,
здесь  – единичный орт оси
– единичный орт оси  .
.
Вектором углового ускорения будем называть вектор равный производной по времени от вектора угловой скорости:  .
.
Вектор  , как и вектор
, как и вектор  , направлен вдоль оси вращения твердого тела.
, направлен вдоль оси вращения твердого тела.
Уравнение равномерного вращения тела
Вращение тела с постоянной угловой скоростью называется равномерным.  ,
, 
проинтегрируем:  ,
,
 – уравнение равномерного движения тела.
– уравнение равномерного движения тела.
Уравнение равнопеременного вращения тела
Вращение тела, при котором угловое ускорение постоянно, называется равнопеременным вращением.
Если абсолютная величина  увеличивается, то вращение называется равноускоренным, если уменьшается – равнозамедленным.
увеличивается, то вращение называется равноускоренным, если уменьшается – равнозамедленным.

Разделим переменные: 
проинтегрируем  ,
, 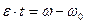 ,
,  ,
,  разделим переменные:
разделим переменные:  .
.
Проинтегрируем:  ,
,  ,
,  .
.
В общем случае:  – уравнение равнопеременного движения тела. Знак "+" соответствует ускоренному вращению, знак "–" – замедленному.
– уравнение равнопеременного движения тела. Знак "+" соответствует ускоренному вращению, знак "–" – замедленному.
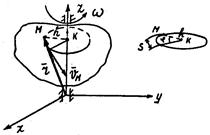
Скорость точки твердого тела,
вращающегося вокруг неподвижной оси
Скорость любой точки тела, вращающегося вокруг неподвижной оси,, называется линейной.
Так как движение точки в этом случае движения тела задано естественным способом, то величина линейной скорости будет:
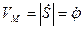
Так как криволинейная координата  ,
,
следовательно,  .
.
Линейная скорость точки вращающегося тела равна произведению угловой скорости тела на расстояние от точки до оси вращения. Направлен вектор скорости точки по касательной к окружности в сторону вращения.
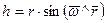

То есть модуль скорости равен модулю векторного произведения  .
.
Направление вектора скорости совпадает с направлением векторного произведения  .
.
То есть, окончательно,  – формула Эйлера.
– формула Эйлера.
Определение ускорения точки тела,
вращающегося вокруг неподвижной оси
Мы доказали, что
 (*)
(*)
Продифференцируем по времени обе части равенства (*):
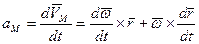 (**)
(**)
Но  ,
, 
Подставим в (**)
 (***)
(***)
Первое слагаемое правой части равенства (***) называется касательным ускорением точки М и обозначается:  .
.
Модуль 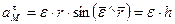
Направлен вектор 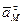 в соответствии с правилом векторного произведения, то есть по касательной к траектории в сторону
в соответствии с правилом векторного произведения, то есть по касательной к траектории в сторону  .
.
Второе слагаемое правой части равенства (***) называется нормальным ускорением точки и обозначается:  .
.
Модуль нормального ускорения

Направлен вектор нормального ускорения всегда к оси вращения. То есть равенство (***) принимает вид:



ЛЕКЦИЯ 8
Сложное движение точки.
Сложным движением точки называется движение точки относительно двух систем отсчета, одна из которых неподвижна, другая произвольно перемещается относительно неподвижной системы координат.

Движение точки М относительно неподвижной системы координат ( ) называется абсолютным. Скорость и ускорение в этом движении называются абсолютной скоростью и абсолютным ускорением, обозначаются
) называется абсолютным. Скорость и ускорение в этом движении называются абсолютной скоростью и абсолютным ускорением, обозначаются  .
.
Движение точки М относительно подвижной системы координат ( ) называется относительным. Скорость и ускорение в этом движении называются относительной скоростью и ускорением, обозначаются
) называется относительным. Скорость и ускорение в этом движении называются относительной скоростью и ускорением, обозначаются  . Подвижная система координат и все, что с ней неразрывно связано, называется переносной средой. Движение точки М вместе с подвижной системой координат относительно неподвижной называется переносным движением.
. Подвижная система координат и все, что с ней неразрывно связано, называется переносной средой. Движение точки М вместе с подвижной системой координат относительно неподвижной называется переносным движением.
Скорость (ускорение) той точки переносной среды, с которой в данный момент времени совпадает наша точка, называется переносной скоростью (ускорением), обозначаются  .
.
Теорема.
Абсолютная производная вектора, определенного в подвижной системе координат, равна геометрической сумме относительной производной этого вектора и векторного произведения угловой скорости подвижных осей координат на этот вектор.
Доказательство:
Пусть вектор 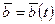 определен в подвижной системе координат,
определен в подвижной системе координат,  – единичные векторы подвижных осей координат, которые вследствие движения подвижной системы координат меняют свое направление.
– единичные векторы подвижных осей координат, которые вследствие движения подвижной системы координат меняют свое направление.
Вектор  можно представить:
можно представить: 
здесь  – проекции вектора
– проекции вектора  на оси подвижной системы координат.
на оси подвижной системы координат.
Продифференцируем обе части записанного равенства
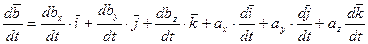 (*)
(*)
Первые три слагаемых правой части (*) называются относительной производной вектора  и обозначаются:
и обозначаются:
 (**)
(**)
Для преобразования трех последних слагаемых (*) воспользуемся формулой Эйлера:  , то есть
, то есть
 (***)
(***)
С учетом (**) и (***) равенство (*) принимает вид:

 (10)
(10)
Теорема сложения скоростей
Абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей.
Доказательство:
Пусть  определяет положение точки М по отношению к
определяет положение точки М по отношению к  ,
,  определяет положение точки С (начало подвижной системы координат) относительно
определяет положение точки С (начало подвижной системы координат) относительно  определяет положение точки М относительно
определяет положение точки М относительно 


Продифференцируем: 

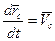
 согласно (10) имеет вид:
согласно (10) имеет вид:  .
.
С учётом всего этого (*) принимает вид:

 – относительная скорость точки М. То есть
– относительная скорость точки М. То есть
 (**)
(**)
Для определения переносной скорости точка М следует закрепить точку в подвижной системе координат, то есть положить в (**)  . Тогда из (**) имеем
. Тогда из (**) имеем  .
.
И равенство (* *) принимает вид:
 (11)
(11)

Модуль абсолютной скорости
 (12)
(12)
Теорема сложения ускорений.
(Теорема Кориолиса)
Абсолютное ускорение точки равно геометрической сумма относительного ускорения, переносного и ускорения Кориолиса,
Доказательство:
Согласно теореме сложения скоростей

Продифференцируем:
 (*)
(*)
Введем обозначения:



Производные  . преобразуем согласно (10)
. преобразуем согласно (10)

Подставим в (*)


 (**)
(**)
Чтобы вычислить переносное ускорение точки М, следует остановить точку в подвижной системе координат, то есть в (**),положить  . Тогда из (**) имеем.
. Тогда из (**) имеем.
 (***)
(***)
С учетом (***) равенство (**) принимает вид:
 (****)
(****)
Удвоенное векторное произведение угловой скорости подвижных осей координат на вектор относительной скорости называется ускорением Кориолиса и обозначается;
 (13)
(13)
Равенство (****) принимав вид:
 (14)
(14)
В общем случае, относительное движение точки есть движение криволинейное, то есть:
 .
.
Переносное движение в общем случае – вращательное
 .
.
То есть (14) принимает вид:
 (15)
(15)
– развернутая форма теоремы Кориолиса. Спроектируем (14) на оси  :
:

Ускорение Кориолиса
Согласно (13) имеем
 (16)
(16)
Ускорение Кориолиса равно нулю, если:
1. 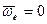 – переносное движение поступательное;
– переносное движение поступательное;
2.  – в те моменты времени, когда относительная скорость обращаете в нуль;
– в те моменты времени, когда относительная скорость обращаете в нуль;
3.  – вектор относительной скорости параллелен вектору угловой скорости переносного вращения.
– вектор относительной скорости параллелен вектору угловой скорости переносного вращения.
Направление  определяется по правилу векторного произведения. Кроме того, направление
определяется по правилу векторного произведения. Кроме того, направление  определяется по правилу Н.Е.Жуковского.
определяется по правилу Н.Е.Жуковского.
Чтобы определить направление вектора ускорения Кориолиса, следует вектор относительной скорости спроектировать на плоскость перпендикулярную вектору угловой скорости переносного вращения, полученный при этом вектор следует повернуть в этой плоскости на угол 90° в сторону 

Причины появления ускорения Кориолиса
 Причиной появления ускорения Кориолиса является взаимное влияние относительного движения на переносное и переносного на относительное. В результате этого влияния переносная скорость меняет модуль и направление, а вектор относительной скорости – направление.
Причиной появления ускорения Кориолиса является взаимное влияние относительного движения на переносное и переносного на относительное. В результате этого влияния переносная скорость меняет модуль и направление, а вектор относительной скорости – направление.
Покажем это на следующем примере.

Пусть по радиусу диска, вращающегося вокруг оси, перпендикулярной плоскости диска, перемещается равномерно человек с относительной скоростью  . Для какого-то фиксированного момента времени
. Для какого-то фиксированного момента времени  , то есть переносная скорость человека – скорость той точки диска, где в данный момент времени находится человек.
, то есть переносная скорость человека – скорость той точки диска, где в данный момент времени находится человек.
Пусть в момент времени  человек занимает положение М1. Очевидно, что за время
человек занимает положение М1. Очевидно, что за время  относительная скорость изменяется по направлению от
относительная скорость изменяется по направлению от  до
до 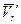 вследствие вращательного переносного движения. Вследствие относительного движения человека из точки М в точку М1 модуль переносной скорости изменился:
вследствие вращательного переносного движения. Вследствие относительного движения человека из точки М в точку М1 модуль переносной скорости изменился:  .
.
Указанные изменения вызывают' появление Кориолисова ускорения.
ЛЕКЦИЯ 9
Плоское движение твёрдого тела.
Движение твердого тела называемся плоским или плоскопараллельным, если все точки тела перемещаются в плоскостях, параллельных некоторой неподвижной плоскости.

Рассмотрим произвольное плоское движение твердого тела. Пусть все точки тела перемещаются в плоскостях, параллельных плоскости  .
.

Из определенен плоского движения и из свойств твердого тела (углы между прямыми, фиксированными в твердом теле, сохраняются неизменными) следует, что любая прямая АВ проведенная в теле перпендикулярно плоскости  , будет перемещаться поступательно, то есть траектории, скорости, ускорения всех точек этой прямой будут одинаковы.
, будет перемещаться поступательно, то есть траектории, скорости, ускорения всех точек этой прямой будут одинаковы.
Таким образом, для определения движения тела необходимо знать движение лишь одной точки на каждой прямой, проведенной перпендикулярно плоскости  . Взяв точки в одной плоскости параллельной плоскости
. Взяв точки в одной плоскости параллельной плоскости  , мы можем утверждать, что плоское движение твердого тела вполне определяется движением плоской фигуры, полученной от пересечения тела любой плоскостью, параллельной плоскости
, мы можем утверждать, что плоское движение твердого тела вполне определяется движением плоской фигуры, полученной от пересечения тела любой плоскостью, параллельной плоскости  .
.
Итак, задание движения тела сводится к заданию движения одного его сечения. Поэтому будем изображать только плоскую фигуру – сечение тела и изучать движение точек этого сечения в его плоскости.

Свяжем жестко с плоской фигурой систему координат  . Тогда положение системы
. Тогда положение системы  , а вместе с ней и плоской фигуры относительно
, а вместе с ней и плоской фигуры относительно  будет определено заданием координат ХА, YА точки А и углом
будет определено заданием координат ХА, YА точки А и углом  между осями АХ2 и АХ (оси АХ2 и АХ соответственно параллельны осям ОХ1 и. OY1 и перемещаются при движении плоской фигуры поступательно).
между осями АХ2 и АХ (оси АХ2 и АХ соответственно параллельны осям ОХ1 и. OY1 и перемещаются при движении плоской фигуры поступательно).
Такал образом, три функции


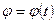
ФОРМУЛА определяют положение плоской фигуры в любой момент времени, то есть это уравнение движения плоской фигуры*
Скорости точек тела при плоском движении.
I способ
Теорема.
Скорость любой точки плоской фигуры равна геометрической суше скорости точки принятой за полюс и скорости данной точки при вращении плоской фигуры вокруг полюса.
Доказательство:
Рассмотрим плоскую фигуру. Точку А примем за полюс. Вычислим скорость точки В.

Радиус-вектор  определяет положение точки В относительно OX1Y1.
определяет положение точки В относительно OX1Y1.
Радиус-вектор  определяет положение точки А относительно OX1Y1.
определяет положение точки А относительно OX1Y1.
Радиус-вектор  определяет положение точки В относительно AX2Y2.
определяет положение точки В относительно AX2Y2.
Очевидно 
Продифференцируем по времени обе части записанного равенства
 (*)
(*)
Заметим, что  – скорость точки В относительно подвижной системы координат AX2Y2. Введем обозначение
– скорость точки В относительно подвижной системы координат AX2Y2. Введем обозначение
 (17)
(17)
Движение тела относительно AX2Y2 представляет собой вращение тела вокруг оси AZ2 перпендикулярной плоскости чертежа. Таким образом, 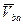 – это скорость точки В при вращении тела вокруг оси, проходящей через полюс А, то есть с учетом формулы Эйлера
– это скорость точки В при вращении тела вокруг оси, проходящей через полюс А, то есть с учетом формулы Эйлера  и равенство (*) принимает вид
и равенство (*) принимает вид
 (18)
(18)
Модуль скорости 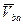 определяется следующим образом;
определяется следующим образом;

При этом вектор 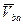 перпендикулярен
перпендикулярен  .
.
II способ
Теорема
Проекции скоростей двух точек плоской фигуры на прямую, их соединяющую – равны.
Доказательство:

Пусть скорость точки А известна –  . Согласно предыдущей теореме для скорости точки В имеем
. Согласно предыдущей теореме для скорости точки В имеем  . Спроектируем обе части этого равенства на ось Х.
. Спроектируем обе части этого равенства на ось Х.  ,
,  , так как
, так как  оси
оси  То есть
То есть
 (19)
(19)
Мгновенный центр скоростей (МЦС)
МЦС называется точка плоской фигуры, скорость которой в, данный момент времени равна нулю.
Теорема
Если угловая скорость плоской фигуры не равна нулю, то МЦС существует.
Доказательство:
Пусть скорость точки. А не равна нулю,  . Вычислим скорость точки Р, отстоящей от точки А на расстоянии
. Вычислим скорость точки Р, отстоящей от точки А на расстоянии  , причем
, причем 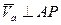 .
.

Согласно I способу  . Так как
. Так как  то
то  , причем
, причем  . Вектор
. Вектор  направлен противоположно
направлен противоположно  , то есть можно записать
, то есть можно записать 
 .
.
Определение скорости точки плоской фигуры с помощью МЦС
III способ.
Выберем за полюс точку Р. Тогда скорость произвольной точки А
 (20)
(20)
Таким образом, скорости точек тела при его плоском движении распределяются так же, как при. вращательном движении тела вокруг неподвижной оси. Роль неподвижной оси играет мгновенная ось, проходящая, через МЦС перпендикулярно плоской фигуре. Следовательно, скорости всех точек плоской фигуры перпендикулярны отрезкам, соединяющим эти точки с МЦС, а модули скоростей пропорциональны расстояниям от точек до МЦС.


Определение угловой скорости плоской фигуры
Угловая скорость плоской фигуры определяется одним единственным способом: она равна скорости любой точки плоской фигуры, деленной на расстояние от этой точки до МЦС:
 (21)
(21)
Частные случаи определения положения МЦС
1. МЦС находится в точке пересечения перпендикуляров к векторам скоростей двух точек плоской фигуры.

2. а) 
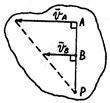
2. б) 

3. 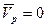

4.  но
но  не перпендикулярна
не перпендикулярна 


Согласно II способу определена скоростей точек
 ,
,  ,
,  .
.
В данный момент времени скорости всех точек плоской фигуры геометрически равны. Имеем мгновенно поступательное распределение; скоростей. Угловая скорость равна нулю. МЦС находится в бесконечности.
ЛЕКЦИЯ 10
Ускорение точек при плоском движении.
Теорема.
Ускорение любой точки плоской фигуры геометрически складывается из ускорения полюса и осестремительного и вращательного ускорений во вращательном движении тела относительно полюса.
Доказательство:
В соответствии с формулой (18) имеем

Продифференцируем последующее равенство по времени:

С учетом (17) это выражение принимает вид:
 (*)
(*)
Два последних слагаемых в равенстве (*) определяют ускорение точки В при закрепленной точке А  . Поэтому их сумма дает ускорение точки В во вращательное движении относительно системы AX2Y2.
. Поэтому их сумма дает ускорение точки В во вращательное движении относительно системы AX2Y2.

 (**)
(**)
Вектор вращательного ускорения точки В во вращательном движении тела относительно полюса А направлен  ВА и определяется формулой
ВА и определяется формулой 
Вектор осестремительного ускорения точки В во движении тела относительно полюса А имеет направление, совпадающее с ВА, т.е. от точки, В к полюсу А, и определяется формулой  .
.
Модули этих составляющих будут
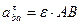

И, окончательно, равенство (*) принимает вид
 (22)
(22)
Мгновенный Центр ускорений (МЦУ)
Мгновенным центром ускорений называется точка плоской фигуры, ускорение которой равно нуля.
Если в данный момент времени задано ускорение какой-то точки А –  , причем
, причем  и
и  известны, то положение МЦУ определяется следующим образом.
известны, то положение МЦУ определяется следующим образом.
Проведем из точки А полупрямую AN под углом  к ускорению
к ускорению  ,отсчитывая этот угол от
,отсчитывая этот угол от  в сторону вращения плоской фигуры, если вращение является ускоренным, и против вращения, если оно замедленное.
в сторону вращения плоской фигуры, если вращение является ускоренным, и против вращения, если оно замедленное.
На полученной полупрямой отложим отрезок  .
.
Полученная таким образом точка Q и есть МЦУ. Убедимся в том, что ускорение точки Q равно нулю.

Выбрав точку А за полюс, получим



Таким образом,  составляет с направлением QA угол
составляет с направлением QA угол  равный углу
равный углу  . Поэтому векторы
. Поэтому векторы  и
и  параллельны. Но в силу принятого правила отсчета угла
параллельны. Но в силу принятого правила отсчета угла  ускорения
ускорения  и
и  направлены противоположно.
направлены противоположно.
Учитывая, что по модулю они равны, получим  .Отсюда следует:
.Отсюда следует: 
ФОРМУЛА
Таким образом, мы доказали, что точка Q – МЦУ.
Ускорение точек плоской фигуры, как ускорение
во вращательном движении вокруг МЦУ
Примем точку Q за полос. На основании (22) имеем
 (23)
(23)
Таким образом, ускорение любой точки плоской фигуры можно определить как ускорение этой точки при вращении вокруг неподвижной оси, проходящей через МЦУ.
Частные случаи определения положения МЦУ
1. Известна точка, ускорение которой равно нулю. Эта точка и является МЦУ.
Например, качение без скольжения колеса по прямолинейному рельсу с постоянной скоростью центра С.

Так как 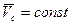 , то
, то  , то есть точка С есть МЦУ. Ускорение любой точки колеса, например точки В, определяется на основании (23)
, то есть точка С есть МЦУ. Ускорение любой точки колеса, например точки В, определяется на основании (23)

Поиск по сайту: