 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
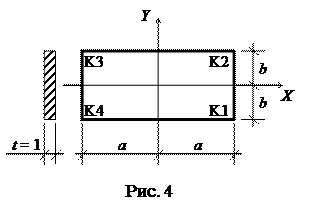
Задание. Для прямоугольной пластинки изображенной на рис.4 требуется:
|
Читайте также: |
Для прямоугольной пластинки изображенной на рис.4 требуется:
1. Найти напряжения  в пластинке.
в пластинке.
2. Определить контурную нагрузку, соответствующую заданной функции напряжений.
3.  Построить эпюры напряжений
Построить эпюры напряжений  для сечений, проходящих через заданную точку
для сечений, проходящих через заданную точку 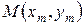 перпендикулярно оси
перпендикулярно оси  и перпендикулярно оси
и перпендикулярно оси  .
.
4. Оценить прочность пластинки в точке 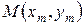 в соответствии с теорией прочности Треска–Сен-Венана и теорией прочности Губера-Мизеса-Генки.
в соответствии с теорией прочности Треска–Сен-Венана и теорией прочности Губера-Мизеса-Генки.
5. Найти деформации  в пластинке.
в пластинке.
6. Построить эпюры деформаций  для сечений, проходящих через точку
для сечений, проходящих через точку 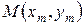 перпендикулярно оси
перпендикулярно оси  и перпендикулярно оси
и перпендикулярно оси  .
.
7. Определить перемещения  в пластинке.
в пластинке.
8. Построить графики перемещений контура пластинки.
9. Построить форму пластинки в состоянии после деформации.
Замечание. Первые четыре пункта задания являются обязательными для выполнения. Пункты 5-9 предназначены для выполнения контрольной работы с элементами НИРС и УИРС по усмотрению преподавателя.
Порядок решения задачи
1. Проверяем корректность постановки задачи. Для этого заданную функцию напряжений подставляем в бигармоническое уравнение (24).
2. Определяем напряжения в пластинке как функции пространственных координат в соответствии с формулами (25).
3. Определяем контурную нагрузку по каждой грани пластинки, используя краевые условия (26).
4. Строим эпюры контурной нагрузки, нормальной к контуру.
5. Строим эпюры контурной нагрузки, касательной к контуру.
6. Строим эпюры напряжений в заданных сечениях.
7. Вычисляем значение эквивалентного напряжения в точке 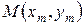 по теории прочности Треска–Сен-Венана (29) и теории прочности Губера-Мизеса-Генки (30) и оцениваем прочность пластинки.
по теории прочности Треска–Сен-Венана (29) и теории прочности Губера-Мизеса-Генки (30) и оцениваем прочность пластинки.
8. Определяем деформации в пластинке как функции пространственных координат в соответствии с обобщённым законом Гука (3).
9. Строим эпюры деформаций в заданных сечениях.
10. Определяем перемещения  в пластинке путём интегрирования соотношений (17).
в пластинке путём интегрирования соотношений (17).
11. Строим графики перемещений контура пластинки.
12. Определяем форму пластинки в состоянии после деформации путем геометрического сложения ординат эпюр перемещений точек контура пластинки.
Пример решения конкретной задачи
Дано:  ;
;
 ,
, 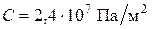 ,
,  ;
;
 - модуль упругости;
- модуль упругости;
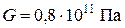 - модуль сдвига;
- модуль сдвига;
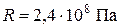 - расчётное сопротивление;
- расчётное сопротивление;
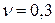 - коэффициент Пуассона материала пластинки;
- коэффициент Пуассона материала пластинки;
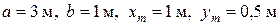 ;
;
 координаты точки
координаты точки  , в которой устанавливается шарнирно-неподвижная опора.
, в которой устанавливается шарнирно-неподвижная опора.
РЕШЕНИЕ
1. Проверяем корректность постановки задачи. Находим выражение производных:
 ,
,  ,
,  .
.
Подставляя полученные производные в бигармоническое уравнение (24) видим, что оно удовлетворяется тождественно. Следовательно, заданная функция  является функцией напряжений плоской задачи теории упругости. Чтобы выяснить, решением какой плоской задачи конкретно является данная функция напряжений, необходимо по данной функции найти значения напряжения и затем по ним определить нагрузку, действующую по граням пластинки.
является функцией напряжений плоской задачи теории упругости. Чтобы выяснить, решением какой плоской задачи конкретно является данная функция напряжений, необходимо по данной функции найти значения напряжения и затем по ним определить нагрузку, действующую по граням пластинки.
Если же, например, в качестве функции напряжений принять функцию 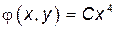 , (С ¹ 0), то
, (С ¹ 0), то

то есть
 .
.
Значит, функция 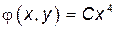 не удовлетворяет бигармоническому уравнению и, следовательно, она не является решением плоской задачи теории упругости.
не удовлетворяет бигармоническому уравнению и, следовательно, она не является решением плоской задачи теории упругости.
2. Определяем напряжения. В соответствии с формулами (25), имеем:
 ,
,
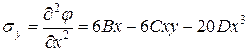 ,
,
 .
.
Учитывая значения коэффициентов  , получаем:
, получаем:
 ,
,
 , (а)
, (а)
 .
.
3.
 |
Определяем контурную нагрузку. Используя граничные условия на контуре (26), подсчитаем интенсивность распределённой внешней нормальной и касательной нагрузки на каждой грани K1-K2, K2-K3, K3-K4, K4-K1 пластинки (рис. 5). Положительные направления внешней контурной нормальной и касательной нагрузки показаны на рис. 5 стрелками с обозначениями
 и
и  .
.
а). Грань K1-K2 пластинки. Внешняя нормаль n к контуру K1-K2 совпадает с направлением оси X, то есть 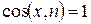 ,
, 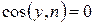 . Все точки стороны K1K2 имеют координаты x и y, причём,
. Все точки стороны K1K2 имеют координаты x и y, причём,  ,
,  . Интенсивность нормальной к контуру нагрузки будет равна
. Интенсивность нормальной к контуру нагрузки будет равна
 ; (б)
; (б)
интенсивность касательной к контуру нагрузки будет равна
 (в)
(в)
б). Грань K2-K3 пластинки. Внешняя нормаль n к контуру K2-K3 совпадает с направлением оси Y, то есть  ,
,  . Все точки стороны K2K3 имеют координаты x и y, причём,
. Все точки стороны K2K3 имеют координаты x и y, причём,  ,
,  . Интенсивность касательной к контуру нагрузки будет равна
. Интенсивность касательной к контуру нагрузки будет равна
 (г)
(г)
интенсивность нормальной к контуру нагрузки будет равна
 (д)
(д)
в). Грань K3-K4 пластинки. Внешняя нормаль n к контуру K3-K4 направлена противоположно направлению оси X, то есть  ,
, 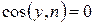 . Все точки стороны K3K4 имеют координаты x и y, причём, ]
. Все точки стороны K3K4 имеют координаты x и y, причём, ]  ,
,  . Интенсивность нормальной к контуру нагрузки будет равна
. Интенсивность нормальной к контуру нагрузки будет равна
 (е)
(е)
интенсивность касательной к контуру нагрузки будет равна
 (ж)
(ж)
г). Грань K4-K1 пластинки. Внешняя нормаль n к контуру K4-K1 направлена противоположно направлению оси Y, то есть  ,
,  . Все точки стороны K4K1 имеют координаты x и y, причём,
. Все точки стороны K4K1 имеют координаты x и y, причём,  ,
,  . Интенсивность касательной к контуру нагрузки будет равна
. Интенсивность касательной к контуру нагрузки будет равна
 (з)
(з)
интенсивность нормальной к контуру нагрузки будет равна
 (и)
(и)
4. Строим эпюры контурной нагрузки, нормальной к контуру. Эпюры контурной нагрузки строим в соответствии с формулами (б, д, е, и) по точкам (рис. 6). При этом учитываем правило знаков для нормальных напряжений: нормальные напряжения считаются положительными, если их направление совпадает с направлением внешней нормали к рассматриваемой площадке и наоборот, если направление напряжений противоположно направлению внешней нормали к площадке, то они считаются отрицательными.
а). Грань K1-K2 пластинки:  ,
,  .
.
б). Грань K2-K3 пластинки:  ,
,  .
.
в). Грань K3-K4 пластинки:  ,
,  .
.
г). Грань K4-K1 пластинки:  ,
,  .
.
Результаты вычислений сведены в табл. 7
 |
Таблица 7

5. Строим эпюры контурной нагрузки, касательной к контуру. Эпюры контурной нагрузки строим в соответствии с формулами (в, г, ж, з) по точкам (рис. 7). При этом учитываем правило знаков для касательных напряжений: касательные напряжения на одной из двух взаимно-перпендикулярных площадок считаются положительными, если их направление совпадает с положительным направлением одной из осей координат, а положительное направление другой оси совпадает с направлением внешней нормали к рассматриваемой площадке; направление касательных напряжений на другой из двух взаимно-перпендикулярных площадок определяется в соответствии с законом парности касательных напряжений. Закон парности касательных напряжений: на любых взаимно-перпендикулярных площадках касательные напряжения равны по величине и направлены так, что стремятся вращать элемент в противоположные стороны. На рис.7 направления внешней контурной касательной нагрузки показаны стрелками.
а). Грань K1-K2 пластинки:  ,
,  .
.
б). Грань K2-K3 пластинки:  ,
,  .
.
в). Грань K3-K4 пластинки:  ,
,  .
.
г). Грань K4-K1 пластинки: 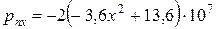 ,
,  .
.
Результаты вычислений сведены в табл. 8
Таблица 8
 |

6. Строим эпюры напряжений в заданных сечениях  и
и  . В сечении
. В сечении  , то есть в сечении, перпендикулярном к оси
, то есть в сечении, перпендикулярном к оси  , строим эпюры напряжений
, строим эпюры напряжений  ,
,  ; в сечении
; в сечении  , перпендикулярным к оси
, перпендикулярным к оси  , – эпюры
, – эпюры  ,
,  .
.
С помощью соотношений (а) находим напряжения:
в сечении  :
:
 (к)
(к)
в сечении  :
:
 (л)
(л)
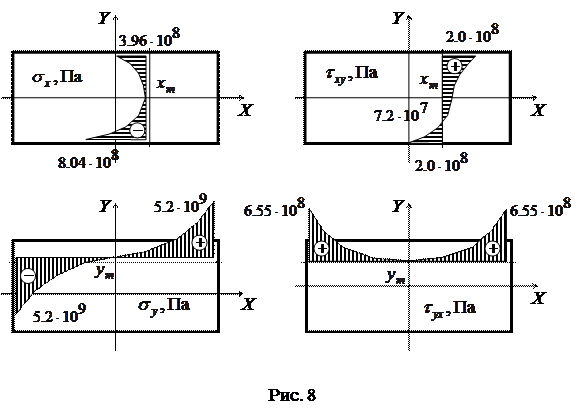
Эпюры напряжений в заданных сечениях строим по точкам. Результаты вычислений сведены в табл. 9. Соответствующие графики представлены на рис. 8.
Таблица 9

 |
7. Вычисляем значение эквивалентного напряжения и оцениваем прочность пластинки в точке 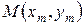 .
.
В соответствии с теорией прочности Треска–Сен-Венана (формула (29)) и соотношениями (а), получаем:

Это означает, что прочность пластинки в точке 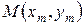 по теории прочности Треска–Сен-Венана не обеспечена.
по теории прочности Треска–Сен-Венана не обеспечена.
В соответствии с теорией прочности Губера-Мизеса-Генки (формула (30)) и соотношениями (а), будем иметь:

Это означает, что прочность пластинки в точке 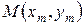 по теории прочности Губера-Мизеса-Генки обеспечена.
по теории прочности Губера-Мизеса-Генки обеспечена.
Таким образом, если нормы проектирования предусматривают оценку прочности пластинки в заданной точке по теории прочности Треска–Сен-Венана, то, поскольку в соответствии с расчётом её прочность в заданной точке не обеспечена, пластинка под действием внешней нагрузки в заданной точке разрушится. Если же нормы проектирования предусматривают оценку прочности пластинки в заданной точке по теории прочности Губера-Мизеса-Генки, то, поскольку в соответствии с расчётом её прочность в заданной точке обеспечена, пластинка будет работать под действием внешней нагрузки без опасности разрушения в заданной точке. Следует отметить, что судить о прочности пластинки в целом можно лишь, вообще говоря, если принятое условие прочности выполняется во всех её точках.
8. Определяем деформации в пластинке. В соответствии с обобщённым законом Гука (3), получаем:
 (м)
(м)
9. Строим эпюры деформаций в заданных сечениях  и
и  . В сечении
. В сечении  , то есть в сечении, перпендикулярном к оси
, то есть в сечении, перпендикулярном к оси  , строим эпюры деформаций
, строим эпюры деформаций  ,
,  ; в сечении
; в сечении  , перпендикулярным к оси
, перпендикулярным к оси  , – эпюры
, – эпюры  ,
,  .
.
С помощью соотношений (м) находим деформации:
в сечении  :
:
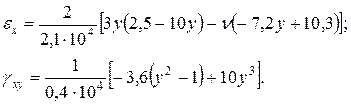 (н)
(н)
в сечении  :
:
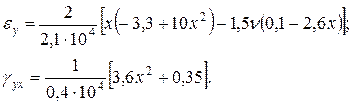 (о)
(о)
Эпюры деформаций в заданных сечениях строим по точкам. Результаты вычислений сведены в табл. 10. Соответствующие графики представлены на рис. 9.
Таблица 10

 |
10. Определяем перемещения  в пластинке. В соответствии с заданием закрепляем точку
в пластинке. В соответствии с заданием закрепляем точку  с помощью шарнирно-неподвижной опоры (рис. 10). Тем самым в точке
с помощью шарнирно-неподвижной опоры (рис. 10). Тем самым в точке  перемещения будут равны нулю:
перемещения будут равны нулю:  .
.
 Интегрируем соотношения (17):
Интегрируем соотношения (17):
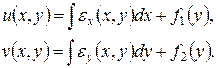 (п)
(п)
Учитывая выражения для деформаций (м), будем иметь:

(р)

Постоянные интегрирования 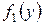 и
и  определяются из условия, что в точке
определяются из условия, что в точке  перемещения равны нулю, то есть
перемещения равны нулю, то есть


Отсюда,


Подставляя полученные значения постоянных интегрирования в соотношения (р) будем иметь функции перемещений:

(с)

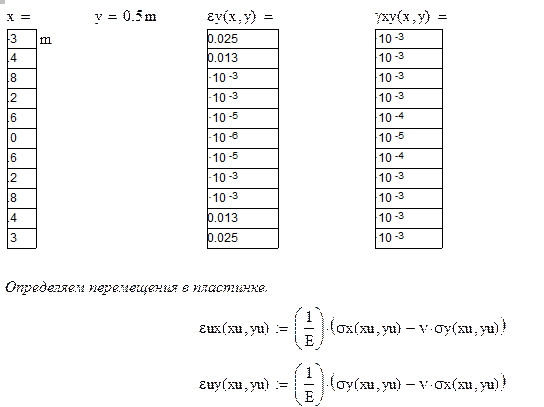
11. Строим графики перемещений контура пластинки. Прежде всего, пользуясь соотношениями (с), определяем вертикальные и горизонтальные перемещения контура пластинки. Затем строим эпюры перемещений вдоль контура пластинки по точкам (рис. 11, 12). Результаты вычислений сведены в табл. 11.
a). Грань K1-K2 пластинки: 


б). Грань K2-K3 пластинки: 

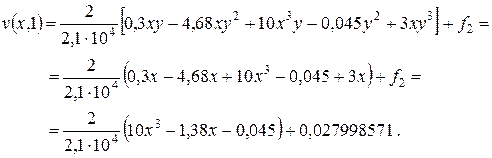
в). Грань K3-K4 пластинки: 


г). Грань K4-K1 пластинки: 


Таблица 11

На рис. 11 представлены эпюры продольных перемещений точек контура пластинки вдоль осей координат X и Y: для стороны K1-K2 – это перемещения  ; для стороны K2-K3 – это перемещения
; для стороны K2-K3 – это перемещения  ; для стороны K3-K4 – это перемещения
; для стороны K3-K4 – это перемещения  ; для стороны K4-K1 – это перемещения
; для стороны K4-K1 – это перемещения  . На рис. 12 представлены эпюры поперечных перемещений точек контура пластинки вдоль осей координат X и Y: для стороны K1-K2 – это перемещения
. На рис. 12 представлены эпюры поперечных перемещений точек контура пластинки вдоль осей координат X и Y: для стороны K1-K2 – это перемещения  ; для стороны K2-K3 – это перемещения
; для стороны K2-K3 – это перемещения  ; для стороны K3-K4 – это перемещения
; для стороны K3-K4 – это перемещения  ; для стороны K4-K1 – это перемещения
; для стороны K4-K1 – это перемещения  .
.
 |
 |
12. Определяем форму пластинки в состоянии после деформации путем геометрического сложения ординат эпюр перемещений точек контура пластинки в соответствии с рис. 11, 12 и таблицей 11.
Замечание: каждая точка контура пластинки получает перемещений и вдоль оси X, и вдоль оси Y. Строя эти перемещения для каждой точки контура пластинки, получаем форму пластинки в состоянии после деформации. Результаты построений представлены на рис. 13.
 |
Решение задачи с использованием математического пакета MathCAD
Ниже, в качестве примера, представлено решение плоской задачи теории упругости при помощи целых полиномов с использованием возможностей математического пакета MathCAD. Эта часть контрольной работы является не обязательной для выполнения.
Ещё раз подчеркнём, что контрольную работу можно выполнять как в режиме ручного счёта, так и на персональном компьютере с использованием математического пакета MachCAD в зависимости от знаний, умений и возможностей студента.










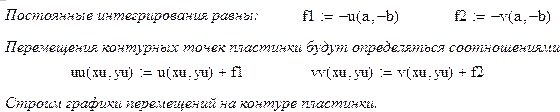


Контрольные вопросы
1. Сформулируйте основные задачи курса теории упругости.
2. Сформулируйте основные допущения, принятые в теории упругости.
3. Что называется напряжением в точке?
4. Какие бывают разновидности напряжений?
5. Объясните понятие “напряжённое состояние в точке”».
6. Какие напряжения называются главными? Какова связь между главными напряжениями?
7. Сформулируйте закон парности касательных напряжений.
8. Какие уравнения устанавливают связь между компонентами напряжения? Запишите эти уравнения.
9. Какие виды деформаций могут возникать в произвольной точке упругого тела?
10. Что называется линейной деформацией?
11. Что называется угловой деформацией?
12. Объясните понятие “деформированное состояние в точке”.
13. Какие деформации называются главными? Какова связь между главными деформациями?
14. Какие перемещения возникают в произвольной точке упругого тела?
15. Какие уравнения устанавливают связь между перемещениями и деформациями? Запишите эти уравнения.
16. Дайте физическую интерпретацию уравнений неразрывности Сен-Венана.
17. Какие уравнения устанавливают связь между напряжениями и деформациями?
18. Что такое модуль упругости, модуль сдвига, коэффициент Пуассона?
19. Сформулируйте обобщённый закон Гука в прямой форме.
20. Сформулируйте закон Гука в форме Ляме.
21. Дайте понятие пространственной и плоской задачи теории упругости?
22. Какие группы уравнений включает общая система уравнений теории упругости?
23. Сформулируйте условия на границе деформированного тела в перемещениях.
24. Сформулируйте условия на границе деформированного тела в напряжениях.
25. Что такое “прямая задача теории упругости”?
26. Как решается прямая задача теории упругости в напряжениях?
27. Как решается прямая задача теории упругости в перемещениях?
28. Что такое “обратная задача теории упругости”?
29. Как решается обратная задача теории упругости?
30. Что называется плоской задачей теории упругости? Охарактеризуйте плоскую деформацию и плоское напряжённое состояние.
31. Запишите уравнения равновесия для плоской задачи.
32. Запишите уравнения Коши для плоской задачи.
33. Запишите уравнение неразрывности деформаций для плоской задачи.
34. Как формулируются физические уравнения для плоской задачи?
35. Сформулируйте граничные условия для плоской задачи в перемещениях, в напряжениях.
36. Какие существуют методы решения плоской задачи теории упругости?
37. Как решается плоская задача в перемещениях?
38. Как решается плоская задача в напряжениях?
39. Какие величины связывает уравнение Мориса-Леви?
40. Что такое функция напряжений?
41. Как при помощи функции напряжений найти напряжения?
42. Запишите бигармоническое уравнение плоской задачи теории упругости.
43. Запишите граничные условия (условия на контуре пластины) с использованием функции напряжений.
44. Какие существуют пути решения плоской задачи теории упругости в напряжениях?
45. Как решается плоская задача теории упругости в напряжениях при помощи целых полиномов?
46. Как проверить, может ли функция напряжений в виде целого полинома быть принята в качестве функции напряжений?
47. Заданы функции: а). 
б). 
Можно ли их принять в качестве функции напряжений?
48. Заданы функции напряжений: а). 
б). 
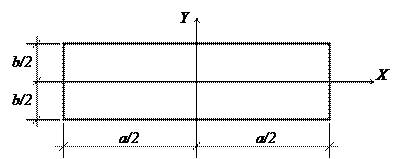 |
Найдите напряжения и постройте их эпюры на контуре пластины (см. рис.)
49. Для чего нужны теории прочности?
50. Что называется расчётным сопротивлением материала?
51. Как определяется расчётное сопротивление для пластичных и хрупких материалов?
52. Какие эксперименты положены в основу построения классических теорий прочности?
53. Сформулируйте первую теорию прочности.
54. Сформулируйте вторую теорию прочности.
55. Сформулируйте третью теорию прочности.
56. Сформулируйте теорию прочности Губера-Мизеса-Генки.
57. Что называется эквивалентным напряжением?
58. Запишите критерий прочности Треска–Сен-Венана для плоской задачи теории упругости.
59. Запишите критерий прочности Губера-Мизеса-Генки для плоской задачи теории упругости.
Поиск по сайту: