 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО МЕХАНИКЕ
 1.1. Точка движется по дуге радиуса ρ со скоростью, зависящей от дуговой координаты l по закону
1.1. Точка движется по дуге радиуса ρ со скоростью, зависящей от дуговой координаты l по закону  , где k – постоянная. Найти угол между векторами полного и тангенциального ускорений как функцию координаты l.
, где k – постоянная. Найти угол между векторами полного и тангенциального ускорений как функцию координаты l.
 ρ
ρ
|
| a -? |
Решение. Угол a можно найти из условия: tga =  ; где
; где 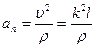 ;
; 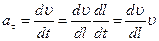 ; подставляя
; подставляя  , получим
, получим 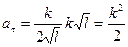 , Þ tga =
, Þ tga =  . Ответ: tga =
. Ответ: tga =  .
.
 1.2. Тело массой m бросили под углом a к горизонту с начальной скоростью
1.2. Тело массой m бросили под углом a к горизонту с начальной скоростью  . Пренебрегая сопротивлением воздуха, найти приращение импульса
. Пренебрегая сопротивлением воздуха, найти приращение импульса  тела за время полета.
тела за время полета.
 a
a
|
 -? -?
|
Решение. Из II-го закона Ньютона Þ  . Интегрируем:
. Интегрируем: 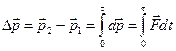 , где
, где  , поскольку в отсутствие трения других сил во время полета нет. Поэтому
, поскольку в отсутствие трения других сил во время полета нет. Поэтому 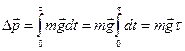 , где мы вынесли постоянные величины из-под интеграла. Так как t - полное время полета, то t/ 2 – это время подъема до наивысшей точки траектории, где вертикальная составляющая скорости становится равной нулю:
, где мы вынесли постоянные величины из-под интеграла. Так как t - полное время полета, то t/ 2 – это время подъема до наивысшей точки траектории, где вертикальная составляющая скорости становится равной нулю: 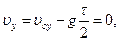 Þ
Þ 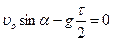 . Откуда находим t =
. Откуда находим t = 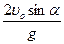 и подставляем его в выражение для
и подставляем его в выражение для 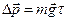 ,
,  , т.е. направлено вниз.
, т.е. направлено вниз.
Ответ: 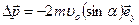 , где последний вектор – орт оси y.
, где последний вектор – орт оси y.
 1.3. Тело бросили под углом a к горизонту с начальной скоростью
1.3. Тело бросили под углом a к горизонту с начальной скоростью  =20 м/с под углом a =30о к горизонту. Пренебрегая сопротивлением воздуха, найти для момента времени t =1,5 c после начала движения нормальное и тангенциальное ускорения.
=20 м/с под углом a =30о к горизонту. Пренебрегая сопротивлением воздуха, найти для момента времени t =1,5 c после начала движения нормальное и тангенциальное ускорения.
 =20 м/с
a =30о
t 1 = 1,5 c =20 м/с
a =30о
t 1 = 1,5 c
|
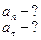
|
Решение. 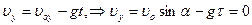 в высшей точке, время достижения которой t =
в высшей точке, время достижения которой t =  =1,02 с < t 1, Þ точка, в которой мы ищем ускорения, находится на спуске. В этой точке
=1,02 с < t 1, Þ точка, в которой мы ищем ускорения, находится на спуске. В этой точке 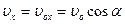 ;
;  ,Þtg j =
,Þtg j =  , где j - одновременно угол между нормальным и полным ускорениями (см. взаимно перпендикулярные стороны). Поскольку полное ускорение равно
, где j - одновременно угол между нормальным и полным ускорениями (см. взаимно перпендикулярные стороны). Поскольку полное ускорение равно 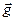 , Þ
, Þ
Ответ:  =9,47 м/с 2;
=9,47 м/с 2;  =2,58 м/с 2
=2,58 м/с 2
1.4. Тело массой m бросили под углом a к горизонту с начальной скоростью  . Пренебрегая сопротивлением воздуха, найти приращение момента импульса D
. Пренебрегая сопротивлением воздуха, найти приращение момента импульса D  тела за время t.
тела за время t.
 a
t
a
t
|
D  -? -?
|
Решение. Примем точку бросания за начало отсчета декартовой системы координат. Относительно этой точки момент импульса  , где
, где  ;
; 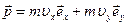 , ибо движение происходит в плоскости xy. Представим векторное произведение в виде определителя матрицы
, ибо движение происходит в плоскости xy. Представим векторное произведение в виде определителя матрицы  =
=  . Подставим проекции: x = u ocos at; y = u osin at - gt 2 / 2;
. Подставим проекции: x = u ocos at; y = u osin at - gt 2 / 2;  ;
;  , тогда
, тогда  =
=  . Поскольку в момент бросания
. Поскольку в момент бросания 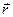 = 0, то и
= 0, то и  1= 0, Þ D
1= 0, Þ D  =
=  . Ответ: D
. Ответ: D  =
= 
1.5. Материальная точка движется вдоль оси х по закону x= At+Bt 3, где А =3 м/с, В =0,06 м/с 3. Найти скорость и ускорение в моменты времени t 1=0, t 2=3 c, а также средние значения скорости и ускорения за первые 3 с движения.
| t 1=0 t 2=3 c А =3 м/с В =0,06 м/с 3 x= At+Bt 3 |
| u 1, u 2 -? a 1, a 2 -? < u>,<a> |
Решение. Проекция скорости на ось х равна  = A+ 3 Bt 2. Подставляя вместо t данные t 1 и t 2, получим u 1=3+3×0,06×02=3 (м/с); u 2=3+3×0,06×32=4,62 (м/с); Проекция ускорения на ось х равна
= A+ 3 Bt 2. Подставляя вместо t данные t 1 и t 2, получим u 1=3+3×0,06×02=3 (м/с); u 2=3+3×0,06×32=4,62 (м/с); Проекция ускорения на ось х равна  = 6 Bt, Þ a 1=6В×0=0; a 2=6×0,06×3=1,08 (м/с 2). Средняя скорость прохождения траектории равна
= 6 Bt, Þ a 1=6В×0=0; a 2=6×0,06×3=1,08 (м/с 2). Средняя скорость прохождения траектории равна 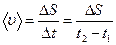 . Поскольку А >0, B >0, Þ тело не меняло направления движения, Þ путь D S равен разности координат: х 2- х 1, или более формально, его можно найти интегрированием скорости:
. Поскольку А >0, B >0, Þ тело не меняло направления движения, Þ путь D S равен разности координат: х 2- х 1, или более формально, его можно найти интегрированием скорости: 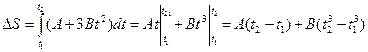 , Þ
, Þ 
 = 3,54 (м/с). Аналогично вычислим среднюю величину ускорения:
= 3,54 (м/с). Аналогично вычислим среднюю величину ускорения:  =
= 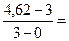 0,54 (м/с 2).
0,54 (м/с 2).
Ответ: u 1=3 м/с; u 2=4,62 м/с; a 1=0; a 2=1,08 м/с 2; < u>= 3,54 (м/с); <a> =0,54 м/с 2.
1.6. Твердое тело замедленно вращается вокруг неподвижной оси с угловым ускорением b, зависящим от угловой скорости w по закону  . Найти среднюю угловую скорость тела за время, в течение которого оно будет вращаться, если в начальный момент угловая скорость = w 0.
. Найти среднюю угловую скорость тела за время, в течение которого оно будет вращаться, если в начальный момент угловая скорость = w 0.
t 1=0
w (t 1)= w 0

|
| < w> -? |
Решение. По определению средняя угловая скорость за интервал от t 1=0 до времени остановки t 2 (пока неизвестного) равна < w> = 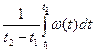 , где последний интеграл равен углу поворота за тот же интервал времени, Þ < w> =
, где последний интеграл равен углу поворота за тот же интервал времени, Þ < w> =  . В проекциях на ось вращения должно быть b = -
. В проекциях на ось вращения должно быть b = -  , где b >0, а знак минус показывает, что вращение замедленное. По определению
, где b >0, а знак минус показывает, что вращение замедленное. По определению 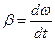 , Þ
, Þ  = -
= -  . Преобразуем последнее уравнение:
. Преобразуем последнее уравнение: 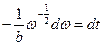 , и проинтегрируем с учетом того, что в момент остановки угловая скорость равна нулю:
, и проинтегрируем с учетом того, что в момент остановки угловая скорость равна нулю:  , Þ
, Þ 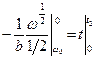 , Þ D t = t 2 =
, Þ D t = t 2 =  . Угол поворота D j =
. Угол поворота D j = 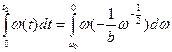 =
=  . Выпишем для удобства полученные соотношения:
. Выпишем для удобства полученные соотношения:
D t =  ; D j =
; D j =  . Откуда следует, что < w> =
. Откуда следует, что < w> =  =
=  . Ответ: < w> =
. Ответ: < w> =  .
.
1.7. Движение материальной точки в плоскости xy описывается уравнениями x = At; y = At (1+Bt), где А и В – положительные постоянные. Определить уравнение траектории материальной точки y (x); радиус-вектор как функцию времени; скорость и модуль скорости; ускорение в зависимости от времени.
| x = At y = At (1+Bt) А> 0, B >0 |
y (x), 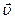 , u, , u,
 , а, , а,
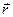 -? -?
|
Решение. Из x = At следует, что 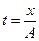 , подставим в выражение для y = At (1+Bt), Þ
, подставим в выражение для y = At (1+Bt), Þ  , Þ
, Þ 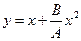 . Это – уравнение траектории. Для точки, движущейся в плоскости xy, радиус-вектор
. Это – уравнение траектории. Для точки, движущейся в плоскости xy, радиус-вектор 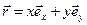 , Þ
, Þ 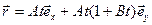 .
. 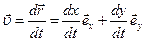 , Þ
, Þ  . Модуль этого вектора найдем по теореме Пифагора:
. Модуль этого вектора найдем по теореме Пифагора:  . Ускорение
. Ускорение 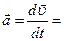 =
= 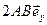 . Модуль ускорения а =2 АВ. Ответ:
. Модуль ускорения а =2 АВ. Ответ: 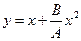 ;
; 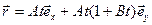 ;
;  ;
; 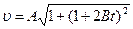 ; а =
; а = 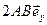 ; а =2 АВ.
; а =2 АВ.
1.8. Твердое тело вращается вокруг неподвижной оси по закону 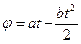 , где a, b – положительные константы. Найти момент времени, в который направление вращения меняется на противоположное.
, где a, b – положительные константы. Найти момент времени, в который направление вращения меняется на противоположное.
 a >0
b >0
a >0
b >0
|
| t -? |
Решение. Если направление вращения изменилось на противоположное, угловая скорость вращения должна изменить знак проекции на ось вращения. В этот момент тело должно остановиться, т.е. w = 0. По определению 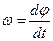 , Þ время t
, Þ время t
находим из условия  , Þ
, Þ 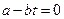 , Þ t =
, Þ t =  . Ответ: t =
. Ответ: t =  .
.
1.9. Якорь электродвигателя, имеющий частоту вращения n =50 c-1, после выключения тока, сделав N = 500 оборотов, остановился. Определить угловое ускорение b якоря.
| n =50 c-1 N = 500 |
| b -? |
Решение. Считая движение якоря равнозамедленным, запишем зависимость угла поворота от времени:  . Подставляя j = 2 pN, w 0=2 pn, получим
. Подставляя j = 2 pN, w 0=2 pn, получим
2 pN =2 pnt - 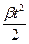 . В момент остановки угловая скорость
. В момент остановки угловая скорость 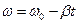 = 0. Поэтому
= 0. Поэтому  , откуда время движения до остановки
, откуда время движения до остановки 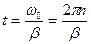 ® 2 pN =2 pnt -
® 2 pN =2 pnt - 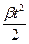 , Þ 2 pN =2 pn
, Þ 2 pN =2 pn 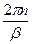 -
-  . После несложных преобразований и сокращений, выразим угловое ускорение
. После несложных преобразований и сокращений, выразим угловое ускорение 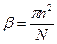 =15,7 (рад/с).
=15,7 (рад/с).
Ответ: b =15,7 рад/с.
1.10. Частица движется по окружности со скоростью 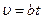 , где b =0,5 м/с2. Найти модуль ее полного ускорения в момент, когда она пройдет n =0,1 длины окружности после начала движения.
, где b =0,5 м/с2. Найти модуль ее полного ускорения в момент, когда она пройдет n =0,1 длины окружности после начала движения.

n =0,1
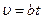 b =0,5 м/с2
b =0,5 м/с2
|
| a -? |
Решение. Представим полное ускорение в виде векторной суммы нормального и тангенциального ускорений: 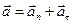 . Тогда модуль полного ускорения равен
. Тогда модуль полного ускорения равен  . По определению
. По определению  , Þ тангенциальное ускорение постоянно. Нормальное ускорение равно
, Þ тангенциальное ускорение постоянно. Нормальное ускорение равно 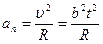 . Пройденный путь S = 0,1×2 pR =
. Пройденный путь S = 0,1×2 pR =  , т.е. 0,2 pR =
, т.е. 0,2 pR = 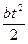 , Þ t 2=
, Þ t 2= 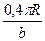 , Þ
, Þ  . Отсюда полное ускорение равно
. Отсюда полное ускорение равно 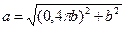 =
= 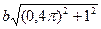 .
.
Ответ: а = 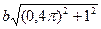 .
.
 1.11. Через блок в виде сплошного диска массой m перекинута нить, к концам которой подвешены грузы с массами m 1 и m 2 (m 2> m 1). Пренебрегая трением, определить ускорение грузов, если их предоставить самим себе.
1.11. Через блок в виде сплошного диска массой m перекинута нить, к концам которой подвешены грузы с массами m 1 и m 2 (m 2> m 1). Пренебрегая трением, определить ускорение грузов, если их предоставить самим себе.
| m m 1 m 2 m 2> m 1 |
| a -? |

 Решение. К каждому грузу приложены: сила тяжести, направленная вниз, и сила натяжения со стороны нити, направленная вверх. Точно такие же по модулю (но противоположные по направлению) силы натяжения со стороны нити приложены с двух сторон к блоку в точках отрыва. Эта пара сил создает вращающий момент. Запишем уравнения второго закона Ньютона для грузов и основное уравнение динамики вращательного движения для диска:
Решение. К каждому грузу приложены: сила тяжести, направленная вниз, и сила натяжения со стороны нити, направленная вверх. Точно такие же по модулю (но противоположные по направлению) силы натяжения со стороны нити приложены с двух сторон к блоку в точках отрыва. Эта пара сил создает вращающий момент. Запишем уравнения второго закона Ньютона для грузов и основное уравнение динамики вращательного движения для диска:
(1)  ; (2)
; (2) 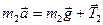 ; (3)
; (3) 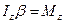 , где последнее уравнение записано сразу в проекции на ось вращения диска, перпендикулярную листу. Спроектируем уравнения (1) и (2) на ось х с учетом того, что правое тело будет двигаться вниз, а левое вверх (т.к. m 2 > m 1):
, где последнее уравнение записано сразу в проекции на ось вращения диска, перпендикулярную листу. Спроектируем уравнения (1) и (2) на ось х с учетом того, что правое тело будет двигаться вниз, а левое вверх (т.к. m 2 > m 1):
(1) 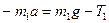 ; (2)
; (2)  . В уравнение (3) подставим момент инерции диска
. В уравнение (3) подставим момент инерции диска 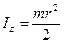 и результирующий момент сил:
и результирующий момент сил: 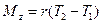 , где r = r 1= r 2 – это радиус диска, равный плечу каждой из сил: (3)
, где r = r 1= r 2 – это радиус диска, равный плечу каждой из сил: (3) 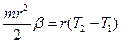 . По модулю ускорение грузов равно ускорению любой точки нерастяжимой нити, в том числе и в точке отрыва нити от диска, а следовательно, и линейному (тангенциальному) ускорению точек на ободе диска. Для этих точек связь между а и b очевидна: а = br, Þ b=
. По модулю ускорение грузов равно ускорению любой точки нерастяжимой нити, в том числе и в точке отрыва нити от диска, а следовательно, и линейному (тангенциальному) ускорению точек на ободе диска. Для этих точек связь между а и b очевидна: а = br, Þ b= 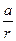 ® (3), Þ (3)
® (3), Þ (3) 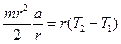 , Þ после сокращений: (3)
, Þ после сокращений: (3) 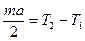 . Теперь вычтем из уравнения (2) уравнение (1):
. Теперь вычтем из уравнения (2) уравнение (1):  , откуда находим сразу разность сил натяжения:
, откуда находим сразу разность сил натяжения: 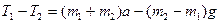 . Изменим знаки на противоположные и подставим в (3):
. Изменим знаки на противоположные и подставим в (3):  ® (3) Þ
® (3) Þ 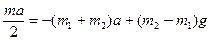 , откуда получим Ответ:
, откуда получим Ответ:  .
.
 1.12. Через легкий блок на конце стола, перекинута невесомая нерастяжимая нить, к концам которой прикреплены грузы, один из которых, m 1=0,6 кг, движется по поверхности стола, а другой m 2=0,4 кг – вертикально вниз. Коэффициент трения груза о стол равен k= 0,1. Найти ускорение грузов и силу натяжения нити.
1.12. Через легкий блок на конце стола, перекинута невесомая нерастяжимая нить, к концам которой прикреплены грузы, один из которых, m 1=0,6 кг, движется по поверхности стола, а другой m 2=0,4 кг – вертикально вниз. Коэффициент трения груза о стол равен k= 0,1. Найти ускорение грузов и силу натяжения нити.
| m 1=0,6 кг m 2=0,4 кг k= 0,1 |
| a -? T -? |
Решение. Запишем второй закон Ньютона для каждого груза:
(1) 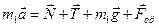
(2) 
Сила натяжения нити по модулю одинакова для обоих грузов, так как нить нерастяжима и массой блока можно пренебречь, Þ для его раскрутки не потребуется момент сил. Модуль силы трения скольжения связан с модулем силы нормальной реакции опоры уравнением  . Спроектируем с учетом этого уравнение (1) на оси х и y, а уравнение (2) – только на ось х:
. Спроектируем с учетом этого уравнение (1) на оси х и y, а уравнение (2) – только на ось х:
(1) ох: 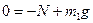 , Þ
, Þ 
(1) oy:  , Þ
, Þ 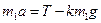
(2) oх: 
Сложив два последних уравнения, исключим T, в результате чего найдем а: 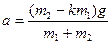 . Подставив а, например, в последнее уравнение, выразим Т:
. Подставив а, например, в последнее уравнение, выразим Т:  .
.
Ответ: а =5,49 м/с 2, Т =2,59 Н.
1.13. На однородный сплошной цилиндр массой m и радиусом R намотана невесомая нить с грузом массой m 1. В момент t =0 система пришла в движение. Пренебрегая трением, найти зависимость кинетической энергии системы от времени.

| m m 1 R |
| К (t)-? |
Решение. Кинетическая энергия системы цилиндр-груз является суммой кинетических энергий поступательного движения груза  и вращательного – цилиндра
и вращательного – цилиндра 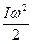 : К =
: К =  +
+ 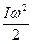 , где
, где  - момент инерции цилиндра:
- момент инерции цилиндра:  =
=  . Связь между линейной и угловой скоростями любой точки на боковой поверхности цилиндра известна:
. Связь между линейной и угловой скоростями любой точки на боковой поверхности цилиндра известна:  , Þ К =
, Þ К =  +
+ 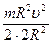 , Þ К =
, Þ К =  . Осталось найти зависимость от времени скорости груза и подставить в последнюю формулу. Из второго закона Ньютона для груза (
. Осталось найти зависимость от времени скорости груза и подставить в последнюю формулу. Из второго закона Ньютона для груза (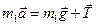 ), который мы спроектируем на ось х (
), который мы спроектируем на ось х (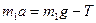 ), и основного уравнения динамики вращательного движения для цилиндра (
), и основного уравнения динамики вращательного движения для цилиндра ( ) можно найти ускорение а, и затем скорость u (t). Подставим в уравнение
) можно найти ускорение а, и затем скорость u (t). Подставим в уравнение  величины:
величины:  =
=  ,
,  ,
, 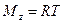 , откуда получим:
, откуда получим: 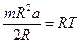 , или, после сокращений
, или, после сокращений 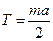 , которое подставим в выражение в рамке и найдем а =
, которое подставим в выражение в рамке и найдем а =  . При равноускоренном движении из состояния покоя
. При равноускоренном движении из состояния покоя  , Þ
, Þ  , Þ
, Þ  . Ответ: К =
. Ответ: К = 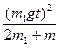 .
.
1.14. Катер массой 200 кг движется по озеру со скоростью 10 м/с. В момент времени t =0 двигатель выключают. Считая силу сопротивления равной - 2 u (Н), найти путь катера до остановки.
| m =200 кг Fc =- 2 u u0 =10 м/с |
| S -? |
Решение. После выключения двигателя единственной силой, действующей на катер, является сила трения, направленная против скорости катера. Из проекции второго закона Ньютона на направление движения:  , можно найти
, можно найти  , а затем проинтегрировать и получить
, а затем проинтегрировать и получить 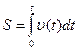 . Однако проще сразу проинтегрировать уравнение
. Однако проще сразу проинтегрировать уравнение 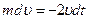 (оно получится из 2-го закона умножением обеих частей на dt):
(оно получится из 2-го закона умножением обеих частей на dt):  , Þ
, Þ  , Þ
, Þ  = 1000 (м). Ответ: S = 1 км.
= 1000 (м). Ответ: S = 1 км.
1.15. Частица массой m движется из начала координат вдоль оси х под действием силы F с=- kx, где k >0. В начальный момент скорость частицы равна u о. Найти зависимость её координаты х от времени.
| m F с=- kx u (0)= uо |
| x (t) -? |
Решение. Запишем второй закон Ньютона в проекции на ось х сразу в форме 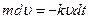 , как мы сделали в предыдущей задаче, и проинтегрируем:
, как мы сделали в предыдущей задаче, и проинтегрируем: 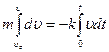 , где последний интеграл – это координата х, с учетом определения скорости и начальных условий. Þ
, где последний интеграл – это координата х, с учетом определения скорости и начальных условий. Þ  , Þ
, Þ 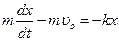 , Þ
, Þ 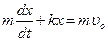 . Это неоднородное дифференциальное уравнение относительно функции x (t). Стандартно оно решается методом Лагранжа. Если Вы ещё не искушены в решении дифференциальных уравнений, то лучше запомнить, что общее решение подобных уравнений
. Это неоднородное дифференциальное уравнение относительно функции x (t). Стандартно оно решается методом Лагранжа. Если Вы ещё не искушены в решении дифференциальных уравнений, то лучше запомнить, что общее решение подобных уравнений 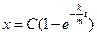 , в чем нетрудно убедиться его прямой подстановкой в уравнение в рамке. Константу С найдем из условия u (0)= uо:
, в чем нетрудно убедиться его прямой подстановкой в уравнение в рамке. Константу С найдем из условия u (0)= uо: 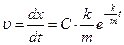 , Þ
, Þ  , Þ С =
, Þ С = 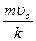 , Þ
, Þ  .
.
Ответ:  .
.
1.16. С платформы, движущейся со скоростью u0 =18 км/час, выстрелили из пушки горизонтально в направлении движения платформы. Масса платформы с пушкой М =15 т, масса снаряда m =20 кг, а начальная скорость снаряда u 2=500 м/с. Найти скорость платформы после выстрела.
| u0 =18 км/час =5 м/с М =15 т=1,5×104 кг m =20 кг u 2=500 м/с |
| u 1 -? |
Решение. Из закона сохранения импульса:  следует, что в проекции на направление движения величины связаны уравнением:
следует, что в проекции на направление движения величины связаны уравнением:  , откуда
, откуда  = 4,34 м/с.
= 4,34 м/с.
Ответ: u 1=4,34 м/с. Поскольку проекция скорости платформы на направление движения, u 1>0, Þ платформа продолжает двигаться в том же направлении.
1.17. Груз массой m =80 кг поднимают с ускорением а =1 м/с 2 по наклонной плоскости с углом наклона a =30о, действуя некоторой силой, направленной вдоль наклонной плоскости вверх. Коэффициент трения скольжения m =0,15; длина наклонной плоскости l = 3 м. Найти: работу силы F; её среднюю мощность; её максимальную мощность, считая начальную скорость груза =0.

| u o=0 m =80 кг а =1 м/с 2 a =30о m =0,15 l = 3 м |
| А-? < P > -? Рmax-? |
Решение. По второму закону Ньютона:
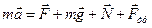 . В проекциях на оси:
. В проекциях на оси:
ох: 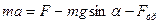 (1)
(1)
oy:  , Þ
, Þ  (2)
(2)
Известно, что модули сил Fтр и N связаны соотношением Fтр = m N ®(1) и (2)®(1), Þ  , откуда найдем F:
, откуда найдем F:  . Так как а =const, и направления силы F и перемещения совпадают, то работа А = F× l, Þ
. Так как а =const, и направления силы F и перемещения совпадают, то работа А = F× l, Þ 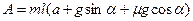 =1,72×103(Дж). Так как движение равноускоренное и пройдено расстояние l, то
=1,72×103(Дж). Так как движение равноускоренное и пройдено расстояние l, то  , Þ
, Þ 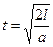 . Отсюда легко найти среднюю мощность:
. Отсюда легко найти среднюю мощность: 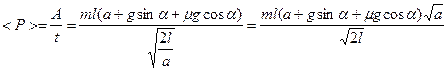 = 702 Вт. Поскольку Р=F×u, то
= 702 Вт. Поскольку Р=F×u, то 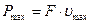 . Максимальной скорость будет в конце пути:
. Максимальной скорость будет в конце пути: 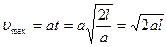 , Þ
, Þ  = 1,41×103 Вт.
= 1,41×103 Вт.
Ответ: А =1,72×103 Дж; < P >=702 Вт; Рmax = 1,41×103 Вт.
1.18. Тело массой m начинает двигаться под действием силы  . Найти зависимость мощности, развиваемой этой силой, от времени.
. Найти зависимость мощности, развиваемой этой силой, от времени.
m

|
| Р (t) -? |
Решение. В общем случае мощность равна скалярному произведению Р =  . Так как
. Так как  , Þ
, Þ 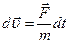 , откуда
, откуда  =
= 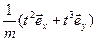 , Þ Р =
, Þ Р = 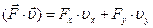 =
= 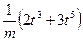 . Ответ: Р (t)=
. Ответ: Р (t)= 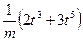 .
.
1.19. На поверхности озера покоится плот массой M и длиной l. Человек массой m переходит с одного конца плота на другой вдоль его длины. Пренебрегая силой трения плота о воду, найти перемещение х плота относительно воды.
| m M l |
| х -? |
Решение. Для системы плот-человек выполняется закон сохранения импульса:  , где
, где 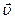 и
и  - скорости человека и плота относительно воды, что в проекции на направление движения человека:
- скорости человека и плота относительно воды, что в проекции на направление движения человека:  , или
, или 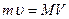 . Скорость человека относительно воды равна
. Скорость человека относительно воды равна 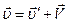 , где
, где 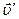 - его скорость относительно плота, что в проекции на то же направление дает
- его скорость относительно плота, что в проекции на то же направление дает 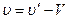 (1). Обратите внимание! Нет принципиальной разницы, равномерно двигались человек и плот, или нет. В последнем случае можно под скоростями понимать средние скорости перемещений. Умножим уравнение (1) на время t, за которое произошло перемещение:
(1). Обратите внимание! Нет принципиальной разницы, равномерно двигались человек и плот, или нет. В последнем случае можно под скоростями понимать средние скорости перемещений. Умножим уравнение (1) на время t, за которое произошло перемещение: 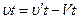 (2). В этом уравнении
(2). В этом уравнении  - перемещение человека относительно воды,
- перемещение человека относительно воды,  - перемещение человека относительно плота и
- перемещение человека относительно плота и 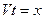 - искомое перемещение самого плота относительно воды, Þ
- искомое перемещение самого плота относительно воды, Þ 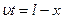 (3). Умножим уравнение в рамке на время t:
(3). Умножим уравнение в рамке на время t: 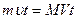 , Þ
, Þ 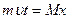 , Þ
, Þ  ®(3), Þ
®(3), Þ 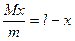 , откуда находим искомое
, откуда находим искомое  . Если необходимо представить ответ в векторном виде, то следует учесть, что плот и человек будут двигаться в противоположные стороны, Þ
. Если необходимо представить ответ в векторном виде, то следует учесть, что плот и человек будут двигаться в противоположные стороны, Þ  , где
, где  - вектор перемещения человека относительно плота.
- вектор перемещения человека относительно плота.
Ответ:  .
.
1.20. Во сколько раз уменьшится скорость шара, двигавшегося со скоростью  , после его соударения с покоящимся шаром, масса которого в n раз больше массы двигавшегося. Удар – центральный, абсолютно упругий.
, после его соударения с покоящимся шаром, масса которого в n раз больше массы двигавшегося. Удар – центральный, абсолютно упругий.
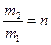

|
 -? -?
|
Решение. Из закона сохранения импульса Þ 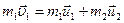 , что в проекции на направление движения первого шара:
, что в проекции на направление движения первого шара: 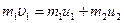 (1); Так как удар абсолютно упругий, то выполняется также и закон сохранения энергии:
(1); Так как удар абсолютно упругий, то выполняется также и закон сохранения энергии:  (2). Учтем в уравнениях (1) и (2), что
(2). Учтем в уравнениях (1) и (2), что  , тогда после сокращений получим:
, тогда после сокращений получим:
 , Þ
, Þ  , Þ
, Þ  (1);
(1);
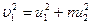 , Þ
, Þ  (2). Поскольку уравнения в рамках имеют одинаковые левые части, значит, равны и правые части:
(2). Поскольку уравнения в рамках имеют одинаковые левые части, значит, равны и правые части: 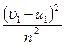 =
= 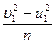 , умножим обе части равенства на n и разложим на множители разность квадратов, Þ
, умножим обе части равенства на n и разложим на множители разность квадратов, Þ  =
=  , сократим на
, сократим на  :
:
 , Þ
, Þ 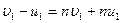 , Þ
, Þ 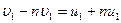 , Þ
, Þ  , Þ
, Þ 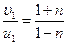 .
.
Ответ: 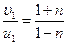 .
.
1.21. К ободу однородного сплошного диска радиусом R приложена постоянная касательная сила F, и, кроме того, действует момент сил трения Мтр. Определить массу диска, если известно, что он вращается с постоянным угловым ускорением b.
| F R Мтр b |
| m -? |
Решение. Сила F создает момент противоположного направления к моменту сил трения, поэтому основное уравнение динамики вращательного движения в проекции на ось вращения запишем так: Ib = FR- Мтр, где I - момент инерции диска I =  , Þ
, Þ 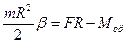 , где неизвестной является только m, Þ
, где неизвестной является только m, Þ 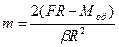 .
.
Ответ: 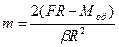 .
.
1.22. Платформа в форме диска вращается по инерции вокруг неподвижной вертикальной оси. На краю платформы стоит человек, масса которого в 3 раза меньше массы платформы. Во сколько раз изменится угловая скорость вращения платформы, если человек приблизится к центру на расстояние, равное половине радиуса платформы.
 n= 3
r=R/ 2 n= 3
r=R/ 2
|
 -? -?
|
Решение. В данной задаче выполняется закон сохранения момента импульса, который в проекции на ось вращения запишем так:  , где I1, I2 – моменты инерции системы человек-платформа до и после перехода; w 1 и w 2 – соответствующие угловые скорости вращения. Отсюда искомое отношение равно:
, где I1, I2 – моменты инерции системы человек-платформа до и после перехода; w 1 и w 2 – соответствующие угловые скорости вращения. Отсюда искомое отношение равно: 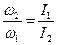 . Моменты инерции системы соответственно равны:
. Моменты инерции системы соответственно равны: 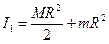 =
= 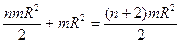 ;
; 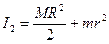 =
= 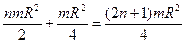 , Þ
, Þ 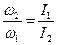 =
=  .
.
Ответ:  =
=  =
= 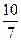 .
.
 1.23. Человек массой m стоит на краю однородного горизонтального диска-платформы массой M, которая может вращаться вокруг вертикальной неподвижной оси, проходящей через центр диска. В некоторый момент человек начал двигаться по краю диска и совершил перемещение на угол
1.23. Человек массой m стоит на краю однородного горизонтального диска-платформы массой M, которая может вращаться вокруг вертикальной неподвижной оси, проходящей через центр диска. В некоторый момент человек начал двигаться по краю диска и совершил перемещение на угол 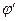 относительно платформы. На какой угол
относительно платформы. На какой угол  при этом перемещении повернулся диск относительно Земли?
при этом перемещении повернулся диск относительно Земли?
m
M
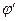
|
 -? -?
|
Решение. За время t поворота диска со средней угловой скоростью < w z> диск повернулся на угол  =< w z> t. Аналогично,
=< w z> t. Аналогично, 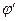 =
= 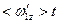 относительно диска. Угловая скорость человека относительно Земли равна разности
относительно диска. Угловая скорость человека относительно Земли равна разности  (1), так как человек и диск будут вращаться в разные стороны. Из закона сохранения момента импульса системы человек-диск в проекции на ось z следует, что
(1), так как человек и диск будут вращаться в разные стороны. Из закона сохранения момента импульса системы человек-диск в проекции на ось z следует, что  где I 1= mR 2, I 2= MR 2/2, Þ
где I 1= mR 2, I 2= MR 2/2, Þ 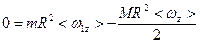 , или
, или  (2). Умножив уравнения (1) и (2) на t, получим:
(2). Умножив уравнения (1) и (2) на t, получим: 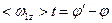 (1);
(1); 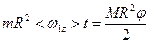 (2). Разделим уравнение (2) на уравнение (1):
(2). Разделим уравнение (2) на уравнение (1): 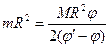 , откуда выражаем искомое φ:
, откуда выражаем искомое φ: 
 .
.
Ответ:  .
.
 1.24. Два шара массами m 1 и m 2 движутся навстречу друг другу со скоростями u 1 и u 2. Определить скорости шаров после удара, кинетическую энергию шаров до и после удара, долю кинетической энергии шаров, превратившуюся во внутреннюю энергию. Удар считать центральным, абсолютно неупругим.
1.24. Два шара массами m 1 и m 2 движутся навстречу друг другу со скоростями u 1 и u 2. Определить скорости шаров после удара, кинетическую энергию шаров до и после удара, долю кинетической энергии шаров, превратившуюся во внутреннюю энергию. Удар считать центральным, абсолютно неупругим.
| m 1, m 2, u 1, u 2 |
u 1-?; u 2-?;
T 1-?; T 2-?;
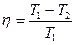
|
Решение. После абсолютно неупругого удара шары движутся как единое целое со скоростью u, направление которой мы не указали, так как оно зависит от соотношения исходных скоростей. Значит, закон сохранения импульса можно записать так:  , откуда сразу в векторном виде можно найти скорость шаров после удара:
, откуда сразу в векторном виде можно найти скорость шаров после удара: 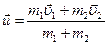 , или в проекции на ось х:
, или в проекции на ось х: 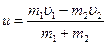 (1). Кинетические энергии системы двух шаров до и после удара соответственно будут:
(1). Кинетические энергии системы двух шаров до и после удара соответственно будут: 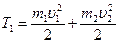 ;
;  . Подставим u из (1):
. Подставим u из (1):
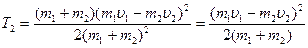 . Тогда
. Тогда  =
= 
 = =
= = 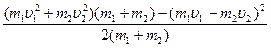 . Подставим в выражение для
. Подставим в выражение для 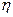 , и после раскрытия скобок и несложных (но не слишком коротких) преобразований, получим:
, и после раскрытия скобок и несложных (но не слишком коротких) преобразований, получим:
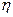 =
=  . Ответ:
. Ответ: 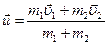 ; u 1= u 2=
; u 1= u 2= 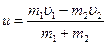 ;
; 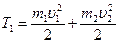 ;
; 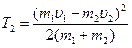 ;
; 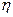 =
=  .
.
1.25. Деревянный стержень массой M = 6 кг и длиной l =2 м может вращаться в вертикальной плоскости относительно горизонтальной оси, проходящей через конец стержня. В другой конец стержня попадает пуля массой m =10 г со скоростью u о=103 м/с, перпендикулярной стержню и оси вращения, и застревает в нем. Найти кинетическую энергию стержня после удара.

| m =10-2 кг M = 6 кг l =2 м u о=103 м/с |
| Т -? |
 Решение. Пуля сначала двигалась прямолинейно, а после попадания в стержень стала участвовать во вращательном движении относительно оси О вместе со стержнем. Поэтому целесообразно использовать закон сохранения момента импульса системы пуля-стержень в проекции на ось вращения:
Решение. Пуля сначала двигалась прямолинейно, а после попадания в стержень стала участвовать во вращательном движении относительно оси О вместе со стержнем. Поэтому целесообразно использовать закон сохранения момента импульса системы пуля-стержень в проекции на ось вращения:  , где I – момент инерции стержня с застрявшей в нем пулей, который» равен моменту инерции одного стержня из-за незначительности массы пули по сравнению с массой стержня:
, где I – момент инерции стержня с застрявшей в нем пулей, который» равен моменту инерции одного стержня из-за незначительности массы пули по сравнению с массой стержня: 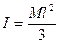 ; w - угловая скорость стержня после попадания пули, Þ
; w - угловая скорость стержня после попадания пули, Þ 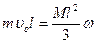 , откуда найдем
, откуда найдем  и подставим в выражение для кинетической энергии (вращения) системы пуля-стержень:
и подставим в выражение для кинетической энергии (вращения) системы пуля-стержень: 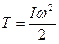 +
+ 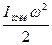 , где вторым слагаемым можно пренебречь по сравнению с первым также из-за незначительности момента инерции пули, обусловленным малой массой пули. Таким образом,
, где вторым слагаемым можно пренебречь по сравнению с первым также из-за незначительности момента инерции пули, обусловленным малой массой пули. Таким образом, 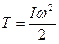 =
= 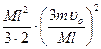 =
=  =25 (Дж). Ответ: Т =
=25 (Дж). Ответ: Т =  = 25 Дж.
= 25 Дж.
1.26. Условие то же. Деревянный стержень массой M = 6 кг и длиной l =2 м может вращаться в вертикальной плоскости относительно горизонтальной оси, проходящей через конец стержня. В другой конец стержня попадает пуля массой m =10 г со скоростью u о=103 м/с, перпендикулярной стержню и оси вращения, и застревает в нем. Найти максимальный угол a, на который стержень отклонится после удара.
| m =10-2 кг M = 6 кг l =2 м u о=103 м/с |
| a -? |
Решение. В предыдущей задаче в момент неупругого удара часть энергии переходила во внутреннюю, поэтому мы не могли использовать закон сохранения энергии. Однако после удара неконсервативных сил в системе нет, Þ к дальнейшему процессу движения стержня и пули можно применить закон сохранения энергии. Если конец стержня при отклонении на угол a окажется приподнятым на высоту 2 h (см. рис. к задаче 1.25), то из подобия треугольников следует, что центр масс стержня (его середина) приподнимется на h. Следовательно в момент остановки стержень приобретет потенциальную энергию Mgh, она же полная энергия. Эта энергия равна кинетической энергии вращательного движения стержня (мы ее вычислили в предыдущей задаче) в момент непосредственно следующий за попаданием пули:  = Mgh. В последнем уравнении неизвестно только h:
= Mgh. В последнем уравнении неизвестно только h:  . Из рис. находим
. Из рис. находим 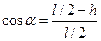 = (1-
= (1- 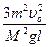 ).
).
Ответ: a =arccos(1- 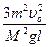 )» 54o.
)» 54o.
 1.27. Однородный шар радиуса r скатывается без скольжения с вершины сферы радиуса R. Найти угловую скорость шара после отрыва от сферы, считая начальную скорость шара равной нулю.
1.27. Однородный шар радиуса r скатывается без скольжения с вершины сферы радиуса R. Найти угловую скорость шара после отрыва от сферы, считая начальную скорость шара равной нулю.
| r R |
| w -? |
Решение. В месте отрыва шара от сферы сила реакции опоры, действующая на шар, равна нулю. Поэтому уравнение движения центра масс шара по окружности радиуса R + r в точке отрыва принимает вид
 .
.
Так как при качении без проскальзывания, сила трения работы не совершает, то выполняется закон сохранения полной механической энергии
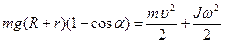 , причем
, причем  . Момент инерции шара известен:
. Момент инерции шара известен: 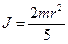 . После подстановки
. После подстановки  в первые два уравнения,
в первые два уравнения, 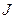 во второе и сокращения на m, останутся два неизвестных:
во второе и сокращения на m, останутся два неизвестных: 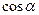 и искомая угловая скорость. Исключая
и искомая угловая скорость. Исключая 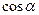 , находим
, находим 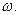
Ответ: 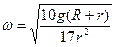
 1.28. Однородный цилиндр толкнули вверх вдоль наклонной плоскости со скоростью
1.28. Однородный цилиндр толкнули вверх вдоль наклонной плоскости со скоростью 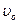 = 3 м/с. Плоскость образует с горизонтом угол 20о. На какую высоту вкатится цилиндр и сколько времени он будет двигаться до первой остановки? Считать, что радиус цилиндра мал по сравнению с высотой и проскальзывания нет.
= 3 м/с. Плоскость образует с горизонтом угол 20о. На какую высоту вкатится цилиндр и сколько времени он будет двигаться до первой остановки? Считать, что радиус цилиндра мал по сравнению с высотой и проскальзывания нет.
a =20o
 = 3 м/с = 3 м/с
|
| h-? t-? |
Решение. Поскольку нет скольжения поверхности цилиндра относительно наклонной плоскости, сила трения качения работы не совершает, следовательно, в системе сохраняется полная механическая энергия. Этот запас энергии в виде суммы кинетической энергии вращения  и кинетической энергии поступательного движения
и кинетической энергии поступательного движения  был сообщен цилиндру у основания наклонной плоскости. В момент достижения максимальной высоты подъема h эта энергия перешла в потенциальную:
был сообщен цилиндру у основания наклонной плоскости. В момент достижения максимальной высоты подъема h эта энергия перешла в потенциальную:
 +
+  =
= 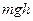 . (1)
. (1)
Поскольку момент инерции цилиндра 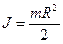 , и в отсутствие проскальзывания
, и в отсутствие проскальзывания 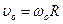 , где
, где 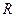 - радиус цилиндра, выражение (1) можно упростить:
- радиус цилиндра, выражение (1) можно упростить: 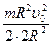 +
+  =
= 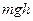 , что после сокращения даст
, что после сокращения даст  +
+  =
= 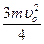 =
= 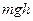 , откуда
, откуда 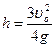 =0,69 м. Время подъема найдем из условия равенства нулю скорости в момент остановки:
=0,69 м. Время подъема найдем из условия равенства нулю скорости в момент остановки:  , Þ
, Þ 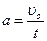 ;
; 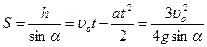 ; Þ
; Þ  , Þ
, Þ 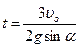 =13,4 с.
=13,4 с.
Ответ: 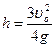 =0,69 м;
=0,69 м; 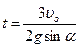 =13,4 с.
=13,4 с.
Поиск по сайту: