 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
по дисциплине «вычислительная математика»
Контрольная работа
Выполнил: студент Роспономарев М.Г.
группы АУЗ – 263с
Шифр 20101664
Проверил: Бочкин А.М.
Волгоград 2012
Содержание
Задание 1. 2
Задание 2. 7
Задание 3. 14
Задание 4. 17
Задание 1
а) Система двух Линейных Алгебраических Уравнений (СЛАУ) с двумя неизвестными задана своей расширенной матрицей. Решите СЛАУ методом Зейделя с точностью до 0,001. Поменяйте порядок следования уравнений в СЛАУ и решите полученную таким образом СЛАУ тем же методом Зейделя. Постройте графики уравнений СЛАУ в обоих случаях и покажите на них первые три-четыре итерации.

Решение
Метод Зейделя представляет собой модификацию метода простой итераций.
Имеем СЛАУ
Ax =b (1)
Предполагая, что aii ≠ 0 разрешим новое уравнение системы (1) относительно x1, второе – относительно x2,…, n-ое уравнение – относительно xn. В результате получим:
x1=β1 - α12x2 - α13x3 -... - α1nxn
x2=β2 - α21x1 - α23x3 -... - α2nxn
xn=βn - αn1xn - αn3x3 -... - αnn-1xn-1
где βi=bi/aii; αij=aij/aii при i ≠ j; αii=0
Известно начальное приближение: x0=(x01, x02,..., x0n).
Основная идея заключается в том, что при вычислении (k+1)-го приближения неизвестной xi учитываются уже вычисленные ранее (k+1) - приближение неизвестных x1, x2,..., xn.
Итерационная схема имеет вид:
xk+11=β1 - ∑α1jxkj
xk+12=β2 - α21xk+11 - ∑α2jxkj
xk+1i=βi - ∑αijxk+11 - ∑α2jxkj
Рассмотрим один из способов преобразования системы: Ax=b, (1), позволяющий всегда получать сходящийся процесс Зейделя. Помножим (1) слева на AT: ATAx=ATb или Cx=d, (2).
где C=ATA; d=ATb.
Систему (2) принято называть нормальной (Такая система получается при использовании МНК).
Нормальная система обладает рядом замечательных свойств:
1) матрица С – симметрическая;
2) все элементы главной диагонали cij > 0;
3) матрица С - положительно определена.
Умножаем матрицы ATA.

Умножаем матрицы ATb.

Приведем к виду:
x1=0.25-0.45x2
x2=-0.0769-1.38x1

Рис. 1. графики уравнений СЛАУ
Покажем вычисления на примере нескольких итераций.
N=1
x1=0.25 - 0 • (-0.45) - 0 • 0=0.25
x2=-0.0769 - 0.25 • (-1.38) - 0 • 0=0.27
x3=0 - 0.25 • 0 - 0.27 • 0=0
N=2
x1=0.25 - 0.27 • (-0.45) - 0 • 0=0.37
x2=-0.0769 - 0.37 • (-1.38) - 0 • 0=0.44
x3=0 - 0.37 • 0 - 0.44 • 0=0
N=3
x1=0.25 - 0.44 • (-0.45) - 0 • 0=0.45
x2=-0.0769 - 0.45 • (-1.38) - 0 • 0=0.54
x3=0 - 0.45 • 0 - 0.54 • 0=0
Остальные расчеты сведем в таблицу.
| N | x1 | x2 | e1 | e2 |
| 0.25 | 0.27 | 0.25 | 0.27 | |
| 0.37 | 0.44 | 0.12 | 0.17 | |
| 0.45 | 0.54 | 0.0755 | 0.1 | |
| 0.49 | 0.61 | 0.047 | 0.0651 | |
| 0.52 | 0.65 | 0.0293 | 0.0406 | |
| 0.54 | 0.67 | 0.0183 | 0.0253 | |
| 0.55 | 0.69 | 0.0114 | 0.0158 | |
| 0.56 | 0.7 | 0.00709 | 0.00982 | |
| 0.56 | 0.7 | 0.00442 | 0.00612 | |
| 0.57 | 0.71 | 0.00275 | 0.00381 | |
| 0.57 | 0.71 | 0.00171 | 0.00237 | |
| 0.57 | 0.71 | 0.00107 | 0.00148 | |
| 0.57 | 0.71 | 0.000666 | 0.000922 |
б) Система четырех Линейных Алгебраических Уравнений (СЛАУ) с четырьмя неизвестными задана своей расширенной матрицей. Решите СЛАУ методом Зейделя с точностью до 0,001.

Решение
Метод Зейделя представляет собой модификацию метода простой итераций.
Имеем СЛАУ
A x =b (1)
Предполагая, что aii ≠ 0 разрешим новое уравнение системы (1) относительно x1, второе – относительно x2,…, n-ое уравнение – относительно xn. В результате получим:
x1=β1 - α12x2 - α13x3 -... - α1nxn
x2=β2 - α21x1 - α23x3 -... - α2nxn
xn=βn - αn1xn - αn3x3 -... - αnn-1xn-1
где βi=bi/aii; αij=aij/aii при i ≠ j; αii=0
Известно начальное приближение: x0=(x01, x02,..., x0n).
Основная идея заключается в том, что при вычислении (k+1)-го приближения неизвестной xi учитываются уже вычисленные ранее (k+1) - приближение неизвестных x1, x2,..., xn.
Итерационная схема имеет вид:
xk+11=β1 - ∑α1jxkj
xk+12=β2 - α21xk+11 - ∑α2jxkj
xk+1i=βi - ∑αijxk+11 - ∑α2jxkj
Рассмотрим один из способов преобразования системы: Ax=b, (1), позволяющий всегда получать сходящийся процесс Зейделя. Помножим (1) слева на AT: ATAx=ATb или Cx=d, (2).
где C=ATA; d=ATb.
Систему (2) принято называть нормальной (Такая система получается при использовании МНК).
Нормальная система обладает рядом замечательных свойств:
1) матрица С – симметрическая;
2) все элементы главной диагонали cij > 0;
3) матрица С - положительно определена.
Умножаем матрицы ATA.
Умножаем матрицы ATb.
Приведем к виду:
x1=0.93+0.6x2+0.74x3+0.69x4
x2=0.73+0.45x1+0.51x3-0.0727x4
x3=0.53+0.66x1+0.6x2+0.36x4
x4=-0.18+0.74x1-0.1x2+0.44x3
Покажем вычисления на примере нескольких итераций.
N=1
x1=0.93 - 0 • 0.6 - 0 • 0.74 - 0 • 0.69=0.93
x2=0.73 - 0.93 • 0.45 - 0 • 0.51 - 0 • (-0.0727)=0.31
x3=0.53 - 0.93 • 0.66 - 0.31 • 0.6 - 0 • 0.36=-0.26
x4=-0.18 - 0.93 • 0.74 - 0.31 • (-0.1) - (-0.26) • 0.44=-0.72
N=2
x1=0.93 - 0.31 • 0.6 - (-0.26) • 0.74 - (-0.72) • 0.69=1.44
x2=0.73 - 1.44 • 0.45 - (-0.26) • 0.51 - (-0.72) • (-0.0727)=0.15
x3=0.53 - 1.44 • 0.66 - 0.15 • 0.6 - (-0.72) • 0.36=-0.25
x4=-0.18 - 1.44 • 0.74 - 0.15 • (-0.1) - (-0.25) • 0.44=-1.13
N=3
x1=0.93 - 0.15 • 0.6 - (-0.25) • 0.74 - (-1.13) • 0.69=1.8
x2=0.73 - 1.8 • 0.45 - (-0.25) • 0.51 - (-1.13) • (-0.0727)=-0.046
x3=0.53 - 1.8 • 0.66 - (-0.046) • 0.6 - (-1.13) • 0.36=-0.22
x4=-0.18 - 1.8 • 0.74 - (-0.046) • (-0.1) - (-0.22) • 0.44=-1.43
Остальные расчеты сведем в таблицу.
| N | x1 | x2 | x3 | x4 | e1 | e2 | e3 | e4 |
| 0.93 | 0.31 | -0.26 | -0.72 | 0.93 | 0.31 | 0.26 | 0.72 | |
| 1.44 | 0.15 | -0.25 | -1.13 | 0.51 | -0.15 | -0.0147 | 0.4 | |
| 1.8 | -0.046 | -0.22 | -1.43 | 0.36 | -0.11 | -0.0285 | 0.3 | |
| 2.1 | -0.22 | -0.21 | -1.67 | 0.3 | 0.17 | -0.0115 | 0.25 | |
| 2.37 | -0.37 | -0.21 | -1.89 | 0.27 | 0.15 | -0.000441 | 0.21 | |
| 2.6 | -0.49 | -0.21 | -2.07 | 0.23 | 0.12 | 0.00419 | 0.18 | |
| 2.81 | -0.59 | -0.22 | -2.23 | 0.2 | 0.1 | 0.00551 | 0.16 | |
| 2.98 | -0.68 | -0.22 | -2.37 | 0.18 | 0.0887 | 0.00548 | 0.14 | |
| 3.13 | -0.76 | -0.23 | -2.49 | 0.15 | 0.0762 | 0.00499 | 0.12 | |
| 3.26 | -0.82 | -0.23 | -2.59 | 0.13 | 0.0655 | 0.00439 | 0.1 | |
| 3.38 | -0.88 | -0.24 | -2.68 | 0.11 | 0.0564 | 0.00382 | 0.0879 | |
| 3.47 | -0.93 | -0.24 | -2.75 | 0.0971 | 0.0486 | 0.0033 | 0.0758 | |
| 3.56 | -0.97 | -0.24 | -2.82 | 0.0837 | 0.0419 | 0.00285 | 0.0653 | |
| 3.63 | -1 | -0.24 | -2.88 | 0.0721 | 0.0361 | 0.00245 | 0.0562 | |
| 3.69 | -1.04 | -0.25 | -2.92 | 0.0621 | 0.0311 | 0.00211 | 0.0485 | |
| 3.75 | -1.06 | -0.25 | -2.97 | 0.0535 | 0.0268 | 0.00182 | 0.0417 | |
| 3.79 | -1.09 | -0.25 | -3 | 0.0461 | 0.0231 | 0.00157 | 0.036 | |
| 3.83 | -1.11 | -0.25 | -3.03 | 0.0397 | 0.0199 | 0.00135 | 0.031 |
Задание 2
Отделить корни уравнения f(x), используя графико-аналитический метод. Найти корни уравнения с заданной точностью методом бисекций, Ньютона или простых интерций. Выполнить проверку правильности найденных решений, вычислив невязки.

Решение

Строим график функции 
| x | y |
| -15 | -3563 |
| -14 | -2920 |
| -13 | -2361 |
| -12 | -1880 |
| -11 | -1471 |
| -10 | -1128 |
| -9 | -845 |
| -8 | -616 |
| -7 | -435 |
| -6 | -296 |
| -5 | -193 |
| -4 | -120 |
| -3 | -71 |
| -2 | -40 |
| -1 | -21 |
| -8 | |

Рис. 1. График функции
Анализируя полученное изображение графика, можно сказать, что уравнение  имеет один корень – это видно из пересечения графика функции
имеет один корень – это видно из пересечения графика функции  с осью OX. Можно выбрать отрезок, содержащий данный корень: [0,5;1] – отрезок изоляции.
с осью OX. Можно выбрать отрезок, содержащий данный корень: [0,5;1] – отрезок изоляции.
Для подтверждения полученных данных, можно решить эту же задачу вторым способом. Для этого необходимо уравнение  преобразовать к виду:
преобразовать к виду:  . Затем следует каждую часть уравнения рассмотреть как отдельную функцию. Т. е.
. Затем следует каждую часть уравнения рассмотреть как отдельную функцию. Т. е. 
| x | y1 | y2 |
| -15 | -3375 | |
| -14 | -2744 | |
| -13 | -2197 | |
| -12 | -1728 | |
| -11 | -1331 | |
| -10 | -1000 | |
| -9 | -729 | |
| -8 | -512 | |
| -7 | -343 | |
| -6 | -216 | |
| -5 | -125 | |
| -4 | -64 | |
| -3 | -27 | |
| -2 | -8 | |
| -1 | -1 | |
| -4 | ||
| -16 | ||
| -28 | ||
| -40 | ||
| -52 | ||
| -64 | ||
| -76 | ||
| -88 | ||
| -100 | ||
| -112 | ||
| -124 | ||
| -136 | ||
| -148 | ||
| -160 | ||
| -172 |

Рис. 2. Наложение искомых функций
Анализируя полученный результат, можно сказать, что точка пересечения двух графиков попадает на тот же самый отрезок изоляции [0,5;1], что и при решении задачи первым способом.
Сделаем крупнее масштаб.
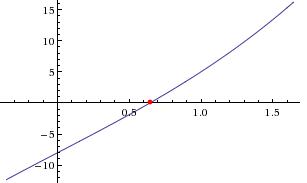
Рис. 3. Увеличенный масштаб
При увеличенном масштабе, корень уравнения х=0,644.
Метод бисекции (метод половинного деления). Пусть мы отделили корень на отрезке 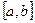 . Разделим отрезок
. Разделим отрезок 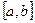 пополам точкой
пополам точкой 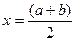 . Если
. Если  , то возможны два случая: либо
, то возможны два случая: либо  меняет знак на отрезке
меняет знак на отрезке  , либо на отрезке
, либо на отрезке  . Выбираем в каждом случае тот из отрезков, на котором функция меняет знак, и продолжаем процесс деления до тех пор, пока
. Выбираем в каждом случае тот из отрезков, на котором функция меняет знак, и продолжаем процесс деления до тех пор, пока  , где
, где  - точность.
- точность.




Таким, образом х=0,644
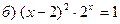
Строим график функции 
| x | y |
| -15 | -0,99118 |
| -14 | -0,98438 |
| -13 | -0,97253 |
| -12 | -0,95215 |
| -11 | -0,91748 |
| -10 | -0,85938 |
| -9 | -0,76367 |
| -8 | -0,60938 |
| -7 | -0,36719 |
| -6 | |
| -5 | 0,53125 |
| -4 | 1,25 |
| -3 | 2,125 |
| -2 | |
| -1 | 3,5 |
| -1 | |
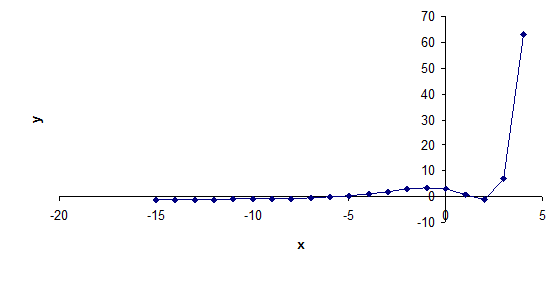
Рис. 1. График функции
Анализируя полученное изображение графика, можно сказать, что уравнение  имеет три кореня – это видно из пересечения графика функции
имеет три кореня – это видно из пересечения графика функции  с осью OX. Можно выбрать несколько отрезков, содержащий данный корень: [-17,5;-16,5], [-6,5;-5,5], [1,5;2,5] – отрезки изоляции.
с осью OX. Можно выбрать несколько отрезков, содержащий данный корень: [-17,5;-16,5], [-6,5;-5,5], [1,5;2,5] – отрезки изоляции.
Для подтверждения полученных данных, можно решить эту же задачу вторым способом. Для этого необходимо уравнение  преобразовать к виду:
преобразовать к виду:  . Затем следует каждую часть уравнения рассмотреть как отдельную функцию. Т. е.
. Затем следует каждую часть уравнения рассмотреть как отдельную функцию. Т. е. 
| x | y1 | y2 |
| -15 | 3,05176E-05 | 0,00346 |
| -14 | 6,10352E-05 | 0,003906 |
| -13 | 0,00012207 | 0,004444 |
| -12 | 0,000244141 | 0,005102 |
| -11 | 0,000488281 | 0,005917 |
| -10 | 0,000976563 | 0,006944 |
| -9 | 0,001953125 | 0,008264 |
| -8 | 0,00390625 | 0,01 |
| -7 | 0,0078125 | 0,012346 |
| -6 | 0,015625 | 0,015625 |
| -5 | 0,03125 | 0,020408 |
| -4 | 0,0625 | 0,027778 |
| -3 | 0,125 | 0,04 |
| -2 | 0,25 | 0,0625 |
| -1 | 0,5 | 0,111111 |
| 0,25 | ||
| 0,25 | ||
| 0,111111 | ||
| 0,0625 | ||
| 0,04 | ||
| 0,027778 | ||
| 0,020408 | ||
| 0,015625 | ||
| 0,012346 | ||
| 0,01 | ||
| 0,008264 | ||
| 0,006944 | ||
| 0,005917 |

Рис. 2. Наложение искомых функций
Анализируя полученный результат, можно сказать, что точки пересечения двух графиков попадает на те же самые отрезки изоляции [-17,5;-16,5], [-6,5;-5,5], [1,5;2,5] – отрезки изоляции, что и при решении задачи первым способом.
Сделаем крупнее масштаб.

Рис. 3. Увеличенный масштаб
При увеличенном масштабе, корень уравнения х=0,644.
Метод бисекции (метод половинного деления). Пусть мы отделили корень на отрезке 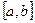 . Разделим отрезок
. Разделим отрезок 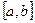 пополам точкой
пополам точкой 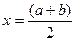 . Если
. Если  , то возможны два случая: либо
, то возможны два случая: либо  меняет знак на отрезке
меняет знак на отрезке  , либо на отрезке
, либо на отрезке  . Выбираем в каждом случае тот из отрезков, на котором функция меняет знак, и продолжаем процесс деления до тех пор, пока
. Выбираем в каждом случае тот из отрезков, на котором функция меняет знак, и продолжаем процесс деления до тех пор, пока  , где
, где  - точность.
- точность.


Таким, образом х=-6
Задание 3
а) Используя обобщенные формулы трапеций и Симпсона вычислить определенные интегралы с заданной точностью. Проверку достижения требуемой точности проводить по правилу Рунге.

Решение
Сначала отрезок интегрирования разбивается на несколько больших отрезков, как правило, на 4-5-6. Разобьем отрезок интегрирования, например, на те же 5 частей.

И шаг, естественно, тоже известен:

В данном случае необходимая точность 0,01. Согласно рекомендации, после запятой для верности оставим пять знаков (можно было и четыре):
| i | ||||||
| xi | ||||||
| f(xi) | 1.809 | 1.689 | 1.607 | 1.546 | 1.5 |
В результате:

После первичного результата количество отрезков удваивают. В данном случае необходимо провести разбиение на 10 отрезков.
Для n= 10 формула трапеций приобретает следующий вид:

Вычислим шаг разбиения:

Результаты расчётов сведём в таблицу:
| i | ||||||
| xi | 4.5 | 5.5 | 6.5 | |||
| f(xi) | 1.891 | 1.809 | 1.743 | 1.689 | 1.645 | |
| i | ||||||
| xi | 7.5 | 8.5 | ||||
| f(xi) | 1.607 | 1.575 | 1.546 | 1.522 | 1.5 |
В результате:

Теперь рассчитаем, на сколько улучшился результат:

Полученная оценка погрешности меньше, чем требуемая точность.
Ответ: 
б) Используя обобщенную формулу Симпсона составить таблицу значений функции, заданной в виде интеграла с переменным верхним пределом.

Решение
Если функция у = f(x) интегрируема на отрезке  , то функция Ф(х) непрерывна на этом отрезке.
, то функция Ф(х) непрерывна на этом отрезке.
Если подынтегральная функция непрерывна, то производная определенного интеграла с переменным верхним пределом существует и равна значению подынтегральной функции для этого предела. т.е.
Сначала отрезок интегрирования разбивается на 8 отрезков. Разобьем отрезок интегрирования, например, на те же 8 частей.

И шаг, естественно, тоже известен:

В данном случае необходимая точность 0,01. Согласно рекомендации, после запятой для верности оставим пять знаков (можно было и четыре):
| i | |||||||||
| xi | 
| 
| 
| 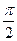
| 
| 
| 
| 
| |
| f(xi) |
Представим таблицу в следующем виде.
| i | |||||||||
| xi | 0,3925 | 0,785 | 1,1775 | 1,57 | 1,9625 | 2,355 | 2,7475 | 3,14 | |
| f(xi) | 0,05706 | 0,0116 | 0,00018 | 3,09E-07 | 6,3E-11 | 1,6E-15 | 5,5E-21 | 2,4E-27 |
В результате:

Ответ: 
Задание 4
а) Найти приближенное решение задачи Коши  методом Эйлера и методом Рунге-Кутта 4 порядка на заданном отрезке с шагом h=0.1 (или h=0.01).
методом Эйлера и методом Рунге-Кутта 4 порядка на заданном отрезке с шагом h=0.1 (или h=0.01).

Решение
Сделаем преобразования:

Расчетные формулы модифицированного метода Эйлера:

Расчетные формулы метода Рунге – Кутта 4 порядка:

| x | y1 | y2 |
| 1,1 | 1,2210 | 1,2221 |
| 1,2 | 1,4923 | 1,4977 |
| 1,3 | 1,8482 | 1,8432 |
| 1,4 | 2,2466 | 2,2783 |
| 1,5 | 2,7680 | 2,8274 |
| 1,6 | 3,4176 | 3,5201 |
| 1,7 | 4,2257 | 4,3927 |
| 1,8 | 5,2288 | 5,4894 |
| 1,9 | 6,4704 | 6,8643 |
| 8,0032 | 8,5834 |
Видно, что самым точным является метод Рунге – Кутта – 8,5834
б) Найти приближенное решение задачи Коши  или
или  методом Эйлера и Рунге-Кутта 4 порядка на отрезке [0;1] с шагом h=0.1 (или h=0.01).
методом Эйлера и Рунге-Кутта 4 порядка на отрезке [0;1] с шагом h=0.1 (или h=0.01).

Решение
Решим задачу модифицированным методом Эйлера и Рунге – Кутта с шагом h=0.1.
Введем функцию: 
Тогда получим следующую задачу Коши для системы двух ОДУ первого порядка:
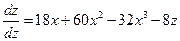
Расчетные формулы модифицированного метода Эйлера:

Расчетные формулы метода Рунге – Кутта 4 порядка:
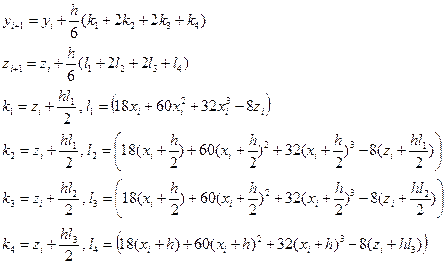
Модифицированный метод Эйлера:
| x | yсv | zcv | y | z | yтеор | zтеор | y-yтеор |
| 0,1 | 4,98 | -0,2 | 4,98 | -0,18 | 4,975 | -0,1462 | 0,016315 |
| 0,2 | 4,78157 | -0,2974 | 4,78977 | -0,2699 | 4,7796 | -0,2461 | 0,015115 |
| 0,3 | 4,58314 | -0,3948 | 4,59954 | -0,3598 | 4,5842 | -0,346 | 0,011915 |
| 0,4 | 4,38471 | -0,4922 | 4,40931 | -0,4497 | 4,3888 | -0,4459 | 0,008715 |
| 0,5 | 4,18628 | -0,5896 | 4,21908 | -0,5396 | 4,1934 | -0,5458 | 0,005515 |
| 0,6 | 3,98785 | -0,687 | 4,02885 | -0,6295 | 3,998 | -0,6457 | 0,002315 |
| 0,7 | 3,78942 | -0,7844 | 3,83862 | -0,7194 | 3,8026 | -0,7456 | -0,00089 |
| 0,8 | 3,59099 | -0,8818 | 3,64839 | -0,8093 | 3,6072 | -0,8455 | -0,00409 |
| 0,9 | 3,39256 | -0,9792 | 3,45816 | -0,8992 | 3,4118 | -0,9454 | -0,00729 |
| 3,19413 | -1,0766 | 3,26793 | -0,9891 | 3,2164 | -1,0453 | -0,01049 |
Схема Рунге - Кутта:
| x | y | z | k1 | l1 | k2 | l2 | k3 | l3 | k4 | l4 |
| -1 | -0,1 | -0,7 | -0,07 | -0,75 | -0,15 | -0,468 | ||||
| 0,1 | 4,98 | -0,18 | -0,18 | -0,6713 | -0,1188 | -0,3422 | -0,1681 | -0,4626 | -0,2374 | -0,1934 |
| 0,2 | 4,78977 | -0,2699 | -0,2699 | -0,3425 | -0,1375 | 0,01564 | -0,2662 | -0,1752 | -0,3249 | 0,0812 |
| 0,3 | 4,59954 | -0,3598 | -0,3598 | -0,0138 | -0,1563 | 0,37346 | -0,3643 | 0,1122 | -0,4123 | 0,3558 |
| 0,4 | 4,40931 | -0,4497 | -0,4497 | 0,31496 | -0,175 | 0,73128 | -0,4624 | 0,3996 | -0,4997 | 0,6304 |
| 0,5 | 4,21908 | -0,5396 | -0,5396 | 0,6437 | -0,1938 | 1,0891 | -0,5605 | 0,687 | -0,5872 | 0,905 |
| 0,6 | 4,02885 | -0,6295 | -0,6295 | 0,97244 | -0,2126 | 1,44692 | -0,6586 | 0,9744 | -0,6746 | 1,1796 |
| 0,7 | 3,83862 | -0,7194 | -0,7194 | 1,30118 | -0,2313 | 1,80474 | -0,7567 | 1,2618 | -0,762 | 1,4542 |
| 0,8 | 3,64839 | -0,8093 | -0,8093 | 1,62992 | -0,2501 | 2,16256 | -0,8548 | 1,5492 | -0,8494 | 1,7288 |
| 0,9 | 3,45816 | -0,8992 | -0,8992 | 1,95866 | -0,2688 | 2,52038 | -0,9529 | 1,8366 | -0,9369 | 2,0034 |
| 3,26793 | -0,9891 | -0,9891 | 2,2874 | -0,2876 | 2,8782 | -1,051 | 2,124 | -1,0243 | 2,278 |
Мax(y-yтеор)=4*10-5
Поиск по сайту: