 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Системы счисления
Язык чисел, как и обычный язык, имеет свой алфавит. В том языке чисел, которым сейчас пользуются практически во всем мире, алфавитом служат десять цифр, от 0 до 9. Этот язык называется десятичной системой счисления. Но не во все времена и не везде люди пользовались десятичной системой. С точки зрения математической она не имеет специальных преимуществ перед другими возможными системами счисления, и своим повсеместным распространением эта система обязана вовсе не общим законам математики, а причинам совсем другого характера.
В последнее время с десятичной системой серьезно конкурирует двоичная система, которой “предпочитают пользоваться” современные вычислительные машины.
Рассмотрим, что представляет собой десятичная система счисления. В этой системе целое положительное число представляется в виде суммы единиц, десятков, сотен и т.д., т.е. в виде суммы различных степеней числа 10 с коэффициентами, которые могут принимать значения от 0 до 9 включительно. Например, запись
означает, что рассматриваемое число содержит 8 единиц, 4 десятка, 5 сотен и 2 тысячи, т.е. 2548 – сокращенная запись выражения
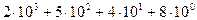 .
.
Однако можно было бы с таким же успехом представить каждое число в виде комбинации степеней не числа 10, а какого-либо другого целого числа (кроме 1), например, числа 7. В этой системе, называемой семеричной, мы бы вели счет от 0 до 6 обычным образом, а число 7 приняли бы за единицу следующего разряда. Его естественно обозначить в семеричной системе символом 10 (единица второго разряда). Чтобы не путать с десятичным числом 10, будем использовать такую запись:
(10)7.
Единицами следующих разрядов должны служить числа 72, 73 и т.д. Их естественно обозначить
(100)7., (1000)7 и т.д.
Любое целое число можно скомбинировать из степеней числа 7, т.е. представить в виде:
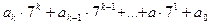 .
.
где каждый из коэффициентов a0, a1,..., ak-1, ak может принимать любое целое значение от 0 до 6. Как и в случае десятичной системы, естественно опускать при записи чисел в системе с основанием 7 сами степени этого основания и писать это число в виде: (ak ak-1... a1 a0)7.
Пример.
Представим десятичное число 2548 в семеричной системе счисления.
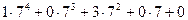 .
.
Таким образом,
(2548)10 = (10300)7.
происхождение десятичной системы счисления
Причины, по которым именно десятичная система счисления оказалась общепринятой, совсем не математического характера. Десять пальцев рук – вот первоначальный аппарат для счета, которым человек пользовался, начиная с доисторических времен. По пальцам удобно считать от одного до десяти. Сосчитав до десяти, т.е. использовав до конца возможности нашего природного "счетного аппарата", естественно принять само число 10 за новую более крупную единицу – единицу следующего разряда. Десять десятков составляют единицу третьего разряда и т.д. таким образом, именно счет по пальцам рук положил начало той системе счисления, которая кажется нам сейчас чем-то самим собой разумеющимся.
другие системы счисления и их происхождение
Десятичная система далеко не сразу заняла то господствующее положение, которое она имеет сейчас. В разные исторические периоды многие народы пользовались системами счисления, отличными от десятичной.
Так, например, довольно широкое распространение имела двенадцатеричная система счисления. Ее происхождение связано, несомненно, тоже со счетом на пальцах. Т. к. четыре пальца руки (кроме большого) имеют в совокупности 12 фаланг, то, перебирая по ним по очереди большим пальцем, и ведут счет от 1 до 12. затем 12 принимается за единицу следующего разряда, и т.д. В устной речи остатки двенадцатеричной системы сохранились и до наших дней: мы часто говорим "дюжина" вместо "двенадцать". Многие предметы (ножи, вилки, столовые приборы…) часто считают именно дюжинами, а не десятками. Сейчас уже крайне редко встречается слово "гросс", означающее "дюжину дюжин" (т.е. единицу третьего разряда в двенадцатеричной системе), но еще несколько десятков лет тому назад оно было широко распространено, особенно в торговом мире. Дюжина гроссов называлась "масса", однако, сейчас такое значение слова "масса" мало кому известно.
Несомненно, остатки двенадцатеричной системы счисления имеются у англичан – в системе мер, например, 1 фут равен 12 дюймам. И в денежной системе – 1 шиллинг равен 12 пенсам.
Заметим, что с математической точки зрения двенадцатеричная система имела бы некоторые преимущества перед десятичной, т.к. число 12 делится на 2,3,4 и 6, а число 10 только на 2 и 5. а больший запас делителей у числа создает известные преимущества в ее использовании.
В древнем Вавилоне, культура которого, в том числе и математическая, была довольно высока, существовала весьма сложная 60-ричная система счисления. Мнения историков на происхождение этой системы расходятся. Одна из гипотез состоит в том, что произошло смешение двух племен, одно из которых пользовалось шестеричной системой, а другое – десятичной. Таким образом, 60-ричная система счисления возникла как компромисс между двумя этими системами. Другая гипотеза состоит в том, что вавилоняне считали продолжительность года равной 360 суткам, что естественно, связывалось с числом 60. однако, это предположение нельзя считать достаточно обоснованным: астрономические познания древних вавилонян были довольно глубокими, поэтому с трудом можно допустить, что погрешность, с которой они определяли продолжительность года, составляла 5 суток.
Несмотря на то, что происхождение 60-ричной системы остается неясным, сам факт ее существования и широкого распространения в Вавилоне установлен и исследован. Примеры использования этой системы, так же как и двенадцатеричной, можно найти и в наши дни: например, в делении часа на 60 минут, минуты – на 60 секунд, в системе измерения углов – 1 градус – 60 минут, … В целом, система, требующая шестидесяти различных цифр, слишком громоздка и менее удобна в использовании, чем десятичная.
По свидетельству известного исследователя Африки Стенли, у ряда африканских племен была распространена пятеричная система счисления. Связь происхождения этой системы со строением человеческой руки – первоначальной "счетной машины" – очевидна.
У ацтеков и майя – народов, населявших в течение многих столетий обширные области американского континента и создавших там высокую культуру, почти полностью уничтоженную испанскими завоевателями в 16-17 вв., была принята двадцатеричная система счисления. Та же двадцатеричная система была принята у кельтов, населявших Западную Европу, начиная со второго тысячелетия нашей эры. Некоторые следы двадцатеричной системы сохранились в современном французском языке. Например, "восемьдесят" буквально переводится как "четырежды двадцать". Число 20 встречается и в бывшей французской денежной системе – один франк делился на 20 су.
Из четырех перечисленных систем (12-ричной, 5-ричной, 60-ричной и 20-ричной), сыгравших наряду с десятичной заметную роль в развитии человеческой культуры. Все, кроме 60-ричной, источники которой неясны, тем или иным способом связаны со счетом по пальцам рук (или рук и ног), т.е. имеют, подобно десятичной системе, несомненное "анатомическое" происхождение.
Как показывают примеры, многие следы этих систем счисления сохранились и до наших дней и в языках многих народов, и в денежных системах, и в системах мер. Однако, для записи чисел и выполнения вычислений, мы всегда пользуемся десятичной системой счисления.
Поиск по сайту: