 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО МОЛЕКУЛЯРНОЙ ФИЗИКЕ И ТЕРМОДИНАМИКЕ
2.1. В сосуде объемом 1 л находится кислород массой 1 г. Определить концентрацию молекул.
 =10-3 м 3
m =1 г = 10-3 кг
М =32×10-3 кг/моль =10-3 м 3
m =1 г = 10-3 кг
М =32×10-3 кг/моль
|
| n -? |
Решение. p = nkT, Þ  .
.  , Þ
, Þ  , подставляем в правую часть выражения в рамке:
, подставляем в правую часть выражения в рамке:  . Ответ: n= 1,88×1025 м -3.
. Ответ: n= 1,88×1025 м -3.
2.2 Найти среднюю скорость молекул идеального газа, плотность которого при давлении 35 кПа равна 0,3 кг / м -3.
| р =35×103 Па r= 0,3 кг / м -3 |
| <u> -? |
Решение. Запишем основное уравнение молекулярно-кинетической теории идеального газа в виде 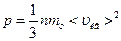 , где mo – масса отдельной молекулы. Средняя скорость равна
, где mo – масса отдельной молекулы. Средняя скорость равна  , а среднеквадратичная
, а среднеквадратичная 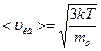 , Þ
, Þ  .
.  , Þ
, Þ  , Þ
, Þ  . Подставим в выражение в рамке:
. Подставим в выражение в рамке:
 . Ответ:
. Ответ:  м/с.
м/с.
2.3. На какой высоте давление составляет 60 % от давления на уровне моря? Считать температуру равной 10 оС, независимо от высоты.
| t= 10 оС p= 0,6 po M =29×10-3 кг/моль |
| h -? |
Решение. Из барометрической формулы  следует, что отношение давлений на высоте h и на уровне моря равно
следует, что отношение давлений на высоте h и на уровне моря равно  , Þ
, Þ  . Обратите внимание: чтобы избавиться от минуса, мы перевернули дробь. Осталось выразить h из последней формулы:
. Обратите внимание: чтобы избавиться от минуса, мы перевернули дробь. Осталось выразить h из последней формулы:  . Ответ: h =4220 м.
. Ответ: h =4220 м.
2.4. Считая температуру равной 273 К и не зависящей от высоты, определить, на какой высоте над уровнем моря плотность воздуха уменьшится в е раз.
| t= 273 К r= 0,6 ro M =29×10-3 кг/моль |
| h -? |
Решение. Из уравнения Клапейрона-Менделеева выразим давление через протность: 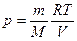 =
=  , и подставим в барометрическую формулу:
, и подставим в барометрическую формулу:  , Þ
, Þ  , Þ
, Þ  , Þ 1=
, Þ 1=  . Отсюда выразим искомую высоту:
. Отсюда выразим искомую высоту:  =8000 м. Ответ: h =8 км.
=8000 м. Ответ: h =8 км.
2.5. В длинном вертикальном сосуде находится смесь из двух газов, у которых массы молекул соответственно равны m 1 и m 2. Концентрации молекул газов у дна сосуда равны соответственно n 01 и n 02. Найти высоту, на которой концентрации газов будут одинаковы. Считать температуру одинаковой по всей высоте.
| n 01 n 02 n 1= n 2 |
| h -? |
Решение. Запишем барометрическую формулу для каждой компоненты смеси:  ;
;  . При n 1= n 2 после несложных преобразований имеем
. При n 1= n 2 после несложных преобразований имеем 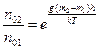 . Логарифмируем последнее выражение, а затем выразим искомую высоту:
. Логарифмируем последнее выражение, а затем выразим искомую высоту:  . Ответ:
. Ответ:  .
.
2.6. Четыре моля кислорода находятся при температуре 27 оС. Найти его внутреннюю энергию.
| t= 27 оС = 300 К n= 4 i =5 |
| U -? |
Решение. Внутренняя энергия идеального газа не зависит от вида газа, а определяется только количеством молей и абсолютной температурой:
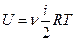 , где для двухатомной жесткой молекулы кислорода число степеней свободы i =5. Отсюда
, где для двухатомной жесткой молекулы кислорода число степеней свободы i =5. Отсюда 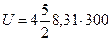 = 25×103 Дж. Ответ: U = 25×103 Дж.
= 25×103 Дж. Ответ: U = 25×103 Дж.
2.7. Определить плотность смеси водорода массой m 1 =8 г и кислорода массой m 2 = 64 г при температуре Т=290 К и давлении 0,1 МПа.
| Т = 290 К р= 0,1 МПа m 1 =8 г =8×10-3 кг m 2 = 64×10-3 кг М 1=2×10-3 кг/моль М 2=32×10-3 кг/моль |
| r -? |
Решение. r= 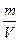 (1), m = m 1+ m 2 (2),
(1), m = m 1+ m 2 (2),  (3), Þ
(3), Þ  (4). Подставляя (2) и (4) в (1), получим искомое выражение для плотности смеси газов:
(4). Подставляя (2) и (4) в (1), получим искомое выражение для плотности смеси газов:  (кг/м 3).
(кг/м 3).
Ответ: r = 0,498 кг/м 3.
2.8. Один моль некоторого идеального газа изобарически нагрели на D Т = 72 К, сообщив ему количество теплоты Q =1,6 кДж. Найти приращение его внутренней энергии и показатель адиабаты 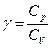 .
.
D Т = 72 К
n= 1
 Q =1,6 кДж
Q =1,6 кДж
|
| D U -? γ -? |
Решение. Количество теплоты, необходимое для нагревания 1 моля газа, равно
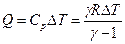 , откуда
, откуда  , откуда, раскрывая скобки, выражаем γ:
, откуда, раскрывая скобки, выражаем γ:
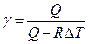 . Приращение внутренней энергии равно
. Приращение внутренней энергии равно  =
=  , где мы подставили ранее найденное γ:
, где мы подставили ранее найденное γ:  .
.
Ответ: D U =1 кДж, γ =1.6
2.9. Идеальный газ с показателем адиабаты γ расширяют так, что сообщаемое ему тепло равно убыли его внутренней энергии. Найти молярную теплоемкость газа в этом процессе и уравнение процесса в параметрах TV.
| γ D Q=- D U |
| С -? T (V) -? |
Решение. По условию  , поэтому молярная теплоемкость равна
, поэтому молярная теплоемкость равна  ,
,  . Это процесс с постоянной теплоемкостью, т.е. политропический. Показатель политропы
. Это процесс с постоянной теплоемкостью, т.е. политропический. Показатель политропы  , где мы подставили найденную выше теплоемкость С. В уравнение политропы в форме
, где мы подставили найденную выше теплоемкость С. В уравнение политропы в форме  =const, подставим n:
=const, подставим n:
 . Ответ:
. Ответ:  ;
;  .
.
2.10. Во сколько раз надо расширить адиабатически газ, состоящий из жестких двухатомных молекул, чтобы их средняя квадратичная скорость уменьшилась в η =1,5 раза?
| η =1,5 i = 5 |
| β -? |
Решение. Обозначим искомое отношение объемов:  . По условию
. По условию  , где слева отношение начальной и конечной среднеквадратичных скоростей, каждая из которых пропорциональна корню квадратному из температуры. Следовательно,
, где слева отношение начальной и конечной среднеквадратичных скоростей, каждая из которых пропорциональна корню квадратному из температуры. Следовательно,  . При адиабатическом процессе
. При адиабатическом процессе  =const, Þ
=const, Þ  =
=  , Þ
, Þ  =
=  , Þ
, Þ  . Осталось подставить показатель адиабаты:
. Осталось подставить показатель адиабаты:  , Þ β =
, Þ β =  .
.
Ответ: 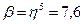 .
.
2.11. Водород совершает цикл Карно. Найти кпд цикла, если при адиабатическом расширении объем газа увеличивается в n =2 раза.
| n =2 γ = 7 / 5 |
| η -? |
Решение. При адиабатическом процессе  =const, Þ
=const, Þ  =
=  , Þ
, Þ  , Þ кпд цикла равен η =
, Þ кпд цикла равен η =  =
=  . Ответ:
. Ответ:  0,25.
0,25.
2.12. Водород совершает цикл Карно. Найти кпд цикла, если при адиабатическом расширении давление газа уменьшается в n =2 раза.
| n =2 γ = 7 / 5 |
| η -? |
Решение. Уравнение адиабаты  =const, Þ
=const, Þ  =
=  , Þ
, Þ  . По условию
. По условию  , Þ
, Þ 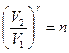 . Из уравнения Клапейрона-Менделеева (
. Из уравнения Клапейрона-Менделеева ( ) следует, что
) следует, что  ;
;  , Þ
, Þ  , что подставляем в формулу для кпд: η =
, что подставляем в формулу для кпд: η =  =
= 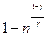 . Ответ:
. Ответ:  =0,18.
=0,18.
2.13. Найти приращение энтропии 1 моля углекислого газа при увеличении его температуры в n =2 раза при изобарическом процессе.
| n =2 p=const n= 1 γ = 7 / 5 |
 -? -?
|
Решение. Энтропия 1 моля идеального газа равна 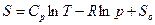 . Следовательно, изменение энтропии при переходе из состояния 1 в состояние 2 равно
. Следовательно, изменение энтропии при переходе из состояния 1 в состояние 2 равно  , где
, где 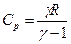 . Жесткая молекула углекислого газа линейна и поэтому имеет 5 степеней свободы, Þ γ = 7 / 5. Окончательно получаем
. Жесткая молекула углекислого газа линейна и поэтому имеет 5 степеней свободы, Þ γ = 7 / 5. Окончательно получаем  (Дж/К). Ответ:
(Дж/К). Ответ:  Дж/К.
Дж/К.
2.14. Один моль кислорода изохорически нагревается от температуры T 1 до температуры T 2=4 T 1. Найти приращение энтропии.
| n =4 V=const n= 1 γ = 7 / 5 |
 -? -?
|
Решение. Запишем энтропию 1 моля идеального газа в фирме  . Тогда изменение энтропии при переходе из состояния 1 в состояние 2 равно
. Тогда изменение энтропии при переходе из состояния 1 в состояние 2 равно  =
=  . Поскольку молекула кислорода линейная, то если считать ее жесткой, то γ = 7 / 5, т.к. число степеней свободы =5. Отсюда Ответ:
. Поскольку молекула кислорода линейная, то если считать ее жесткой, то γ = 7 / 5, т.к. число степеней свободы =5. Отсюда Ответ: 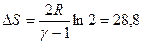 Дж/К.
Дж/К.
2.15. Азот массой 28 г адиабатно расширили в n =2 раза, а затем изобарно сжали до исходного объема. Определить изменение энтропии в ходе указанных процессов.
| n =2 m = 28×10-3 кг i= 5 |
 -? -?
 -? -?
 -? -?
|
Решение. Обозначим адиабатный переход 1®2, а изобарный 2®3. Полное изменение энтропии равно сумме:  =
=  +
+  . Изменение энтропии на участке 1®2:
. Изменение энтропии на участке 1®2:  =0, так как адиабатный процесс идет без теплообмена, Þ
=0, так как адиабатный процесс идет без теплообмена, Þ  , Þ
, Þ  =0. Изменение энтропии на участке 2®3 равно
=0. Изменение энтропии на участке 2®3 равно  =
=  . При р= const
. При р= const  ;
; 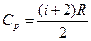 . Подставляя в формулу
. Подставляя в формулу  =
=  , получим:
, получим:  =
=  =
=  . Ответ:
. Ответ:  Дж/К.
Дж/К.
2.16. Считая процесс образования мыльного пузыря изотермическим, определить работу А, которую надо совершить, чтобы увеличить его диаметр от d 1=6 мм до d 2=60 мм. Поверхностное натяжение мыльного раствора принять равным s =40 мН/м.
| d 1=6×10-3 м d 2=60×10-3 м Т=const s =40×10-3 Н/м |
| А -? |
Решение. Величину поверхностного натяжения можно выразить двумя способами: либо как силу натяжения, приходящуюся на единицу длины контура, либо как поверхностную энергию, приходящуюся на единицу площади поверхности:  . В последнем случае, искомую работу следует приравнять изменению энергии в результате раздувания пузыря, а
. В последнем случае, искомую работу следует приравнять изменению энергии в результате раздувания пузыря, а  -полагать изменением площади поверхности с учетом того, что у пузыря две поверхности: внешняя и внутренняя. Таким образом,
-полагать изменением площади поверхности с учетом того, что у пузыря две поверхности: внешняя и внутренняя. Таким образом, 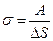 , где
, где 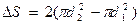 . При Т=const, Þ s=const. Таким образом,
. При Т=const, Þ s=const. Таким образом, 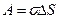 =
=  . Ответ: А =896×10-6 Дж.
. Ответ: А =896×10-6 Дж.
2.17. Капилляр, имеющий внутренний радиус r =0,5 мм, опущен в жидкость. Определить массу жидкости, поднявшейся в капилляре, если ее поверхностное натяжение равно 60 мН/м.
| r =0,5 ×10-3 м s =60×10-3 Н/м |
| m -? |
Решение. Сила тяжести столба жидкости в капилляре уравновешена силами поверхностного натяжения в связи со смачиванием внутренних стенок капилляра жидкостью:  , где l=2pr – длина границы. Отсюда
, где l=2pr – длина границы. Отсюда  .
.
Ответ: m =1,92×10-5 кг .
Поиск по сайту: