Описание структур алгоритмов

Различают следующие структуры:

· линейная;

· разветвляющаяся;

· циклическая;

· вспомогательный алгоритм.

Простейший алгоритм имеет линейную структуру (рис. 1) и схематически может быть представлен в виде схемы, состоящей из пяти блоков (по ГОСТ 19.701-90).

Начало программы (блок 1) определяет ее запуск. Далее происходит ввод данных (блок 2), затем производится обработка информации, т.е. действия над исходными данными (блок 3).Результат этих выводится (блок 4), после чего программа заканчивает свою работу (блок 5).

Например, для нахождения решения функции y=f(x) алгоритм расчета может быть представлен в виде схемы программы (рис. 2)

Рис. 1. Линейная структура алгоритма	Рис. 2. Алгоритм решения функции y=f(x)

Вывод значения х (исходного данного) вместе с выводом y (результатом расчета) облегчает анализ полученного результата (в этом случае можно сопоставить х и у).

Недостатком алгоритма является невозможность произвести расчет по нескольким математическим зависимостям и повторить расчет не покидая программу.

Для нахождения значений функции, заданной на нескольких интервалах можно использовать разветвляющуюся структуру алгоритма. В этом случае схема программы будет содержать один или несколько блоков проверки условий (блоков «решение»).

Рассмотрим решение уравнения.

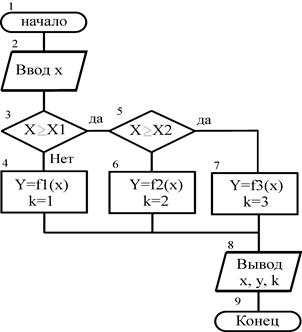
Рис. 3. Алгоритм нахождения значений функции, заданной на нескольких интервалах

В блоке 3 (рис. 3) условие изменено на противоположное с целью применения однотипных действий в алгоритме. Дополнительно введена переменная k, которая имеет значения 1,2,3, что соответствует номеру расчетной формулы и улучшает анализ полученного результата (указывает на ветвь, в которой происходит расчет). Каждый из блоков «решение» имеет по две ветви расчета, соответственно для выполнения условия «да» - «истинно», «нет» - «ложно».

Здесь также невозможно повторить расчет без перезапуска программы. Эту проблему можно решить, организовав циклическую структуру выполнения рассмотренного алгоритма.

Если значение х заранее не известно, то можно организовать алгоритм с использованием логического цикла, позволяющего повторить весь расчет с самого начала.

Рис. 4. Алгоритм для нахождения значений функции с использованием логического цикла

В схеме программы (рис. 4) блок 4 определяет часть программы, изображенной в другом месте. В данном случае имеется в виду часть алгоритмов: линейного (рис. 2) блок 3, или разветвляющегося (рис. 3) (блоки 3,4,5,6,7), связанная с нахождением значения функции.

Блоки 2 и 7 определяют границы логического цикла (начало и конец соответственно). Чтобы можно было однозначно сказать, что эти границы принадлежат одному циклу, они должны иметь уникальное имя, например, «Цикл А». Для выхода из цикла (или продолжения расчета) необходимо ввести значение переменной с (блок 6). Если условие с =0 выполнится, то программа заканчивает работу (цикл завершается), иначе цикл повторяется, начиная с блока 3, где вводится новое значение х. Для того, чтобы пользователь знал, что значение «0» вводится для выхода из программы, ему на экран надо вывести сообщение (блок 5).

В случае, когда количество расчетов заранее известно (или может быть вычислено), например, если задано начальное значение х=х_min, конечное х_max и шаг приращения _D х целесообразнее использовать арифметический цикл (цикл с параметром) (рис. 5)

Рис. 5. Структура арифметического цикла

где х – текущее значение переменной х (параметр цикла), которое меняется в цикле автоматически после каждого расчета на _D х, начиная с х_min (с начального значения). Цикл заканчивается х>x_max.

Недостатком данного алгоритма является то, что y=f(x) для последнего значения х (для х=х_max) может быть не рассчитано, если значение х_min- х_max кратно _D х, т.е. делится на целое число. Это связано с тем, что если значение параметра является действительным числом в силу округления значений, то полученное число будет несколько больше (или меньше) x_max. Этого недостатка можно избежать применением арифметического цикла с целочисленным параметром.

, тогда (рис. 6)

Наиболее точным является алгоритм с заданием исходных данных: х_min, x_max и n – число точек расчета.

, тогда х=х_min+ _D х(i-1),

где n – количество точек расчета значений функций.

Тогда алгоритм примет вид (рис. 7)

Рис. 6. Циклический алгоритм Рис. 7. Циклический алгоритм

Такой алгоритм позволяет данные сохранить в массивах x_i, y_i так, и тем самым разделить расчетные функции и вывод данных. Тогда алгоритм примет следующий вид (рис. 8).

Рис. 8 Циклический алгоритм

В результате комбинаций всех этих структур можно создавать алгоритм любой сложности, при этом на начальном этапе его можно не детализировать. Он может быть представлен в виде подпрограмм (вспомогательных алгоритмов) и простейшие алгоритмы (все представленные ранее) можно изобразить в виде пяти блоков (аналогично линейному алгоритму на рис. 9).

	ПП1 – подпрограмма 1 – ввод исходных данных; ПП2 – подпрограмма 2 – обработка данных; ПП3 – подпрограмма 3 – вывод результатов расчета. Далее приступают к детализации алгоритма. Разработав детальный алгоритм решения поставленной задачи, приступают к программированию ее на алгоритмическом языке.
Рис. 9.Упрощенный вид алгоритма

Поиск по сайту: