 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
МАТЕРИАЛЫ К ЛЕКЦИИ 2
Центры и касательные кривых второго порядка. Оптическое свойство параболы.
Литература. [1]§ 33, 34.
На прошлой лекции мы получили необходимые нам соотношения, которые будем использовать в дальнейшем:
 , (*)
, (*)
где коэффициенты 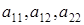 не равны нулю одновременно.
не равны нулю одновременно.
Рассмотрим параметрические уравнения прямой l:
 (1*)
(1*)
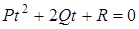 , (2*)
, (2*)
 , (3*)
, (3*)
 , (4*)
, (4*)
 . (5*)
. (5*)
Под центром кривой будем понимать ее центр симметрии. Найдем способ определения ее центра по общему уравнению. Докажем лемму.
Лемма. Пусть прямая задана своими параметрическими уравнениями:  точкам
точкам  и
и  соответствуют параметры
соответствуют параметры 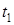 и
и  . Тогда начальная точка
. Тогда начальная точка  в том и только в том случае совпадает с серединой отрезка
в том и только в том случае совпадает с серединой отрезка 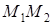 , когда
, когда  .
.
Доказательство. Пусть координаты данных точек  и
и  равны:
равны:  . Тогда
. Тогда
 (1)
(1)
Точка  в том и только в том случае является серединой отрезка
в том и только в том случае является серединой отрезка 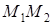 , когда
, когда 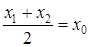 ,
,  Подставим сюда соотношения (1):
Подставим сюда соотношения (1):  ,
,  . Полученные равенства равносильны условию
. Полученные равенства равносильны условию  . Утверждение доказано.
. Утверждение доказано.
Теорема 2. Пусть кривая g второго порядка задана общим уравнением
 .
.
Тогда точка  в том и только в том случае служит центром симметрии g, когда ее координаты удовлетворяют системе уравнений:
в том и только в том случае служит центром симметрии g, когда ее координаты удовлетворяют системе уравнений:
 (2)
(2)
Доказательство. Пусть  - центр симметрии кривой. Тогда любая прямая не асимптотического направления пересекает эту кривую в двух точках
- центр симметрии кривой. Тогда любая прямая не асимптотического направления пересекает эту кривую в двух точках  и
и  , которые симметричны относительно
, которые симметричны относительно  . Если
. Если  - параметрическое уравнение этой прямой, а
- параметрическое уравнение этой прямой, а 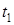 и
и  параметры точек
параметры точек  и
и  , то, согласно доказанной лемме,
, то, согласно доказанной лемме,  . С другой стороны
. С другой стороны 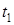 и
и  - корни квадратного уравнения (2*). Тогда по теореме Виета коэффициент Q этого уравнения также равен нулю. Из формулы (4*) получим:
- корни квадратного уравнения (2*). Тогда по теореме Виета коэффициент Q этого уравнения также равен нулю. Из формулы (4*) получим:  , или
, или  . Найденное равенство выполняется для любых a и b. Поэтому оно справедливо только тогда, когда
. Найденное равенство выполняется для любых a и b. Поэтому оно справедливо только тогда, когда  , u и v - решения системы (2).
, u и v - решения системы (2).
Обратно. Рассмотрим произвольное решение u, v системы (2). Обозначим через l - прямую не асимптотического направления, проходящую через точку  . Пусть
. Пусть  ее параметрические уравнения, а
ее параметрические уравнения, а  и
и  ‑ точки пересечения l с кривой. Тогда параметры
‑ точки пересечения l с кривой. Тогда параметры 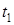 и
и  точек
точек  и
и  являются решением квадратного уравнения (2*). Из формул (4*) и (2) следует, что второй коэффициент Q этого уравнения равен нулю. По теореме Виета
являются решением квадратного уравнения (2*). Из формул (4*) и (2) следует, что второй коэффициент Q этого уравнения равен нулю. По теореме Виета  . Поэтому согласно лемме 1, точка
. Поэтому согласно лемме 1, точка  - середина отрезка
- середина отрезка 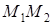 . Так как наши рассуждения справедливы для любой прямой не асимптотического направления, то
. Так как наши рассуждения справедливы для любой прямой не асимптотического направления, то  - центр симметрии кривой g.
- центр симметрии кривой g.
Следствие. Если центр кривой совпадает с началом координат, то  , и ее общее уравнение имеет вид:
, и ее общее уравнение имеет вид: 
Действительно, система (2) имеет нулевое решение, поэтому 
Как легко видеть, определитель системы (2) совпадает с первым инвариантом D кривой. Поэтому кривые эллиптического и гиперболического типов имеют единственный центр симметрии. Они носят название центральных кривых второго порядка. Для кривых параболического типа D = 0. Эти кривые либо не имеют центров симметрии, либо имеют их бесконечно много. Такие кривые называются нецентральными.
Определение 3. Точка кривой второго порядка называется обыкновенной, если она не совпадает с ее центром симметрии. В противном случае она носит название особой.
Легко видеть, что эллипс, гипербола и парабола состоят из обыкновенных точек. Как известно из курса математического анализа, под касательной к кривой в точке  понимается предельное положение секущей
понимается предельное положение секущей 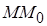 , при условии, что точка М кривой стремится к
, при условии, что точка М кривой стремится к  . Секущая пересекает кривую в двух вещественных точках, она имеет не асимптотическое направление. Так как касательная – предельное положение секущей, то он является прямой, пересекающей кривую в двух совпавших точках и имеющей не асимптотическое направление. Касательные к кривой будем рассматривать только в ее обыкновенных точках.
. Секущая пересекает кривую в двух вещественных точках, она имеет не асимптотическое направление. Так как касательная – предельное положение секущей, то он является прямой, пересекающей кривую в двух совпавших точках и имеющей не асимптотическое направление. Касательные к кривой будем рассматривать только в ее обыкновенных точках.
Теорема 3. Если  - обыкновенная точка кривой второго порядка, заданной своим общим уравнением (*), то уравнение касательной в этой точке имеет вид:
- обыкновенная точка кривой второго порядка, заданной своим общим уравнением (*), то уравнение касательной в этой точке имеет вид:
 (3)
(3)
Доказательство. Касательная пересекает кривую в двух совпавших точках. Обозначим через a и b координаты ее направляющего вектора. Если уравнение прямой имеет параметрический вид (1*): 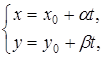 то параметры точек пересечения определяются как решения уравнения (2*). Так как это уравнение имеет единственный корень, то его дискриминант
то параметры точек пересечения определяются как решения уравнения (2*). Так как это уравнение имеет единственный корень, то его дискриминант  равен нулю. Таким образом,
равен нулю. Таким образом,  . По условию точка
. По условию точка  принадлежит кривой. Поэтому из формулы (5*)следует, что
принадлежит кривой. Поэтому из формулы (5*)следует, что  . Итак, прямая l тогда и только тогда является касательной к кривой в ее точке
. Итак, прямая l тогда и только тогда является касательной к кривой в ее точке  , когда координаты
, когда координаты  и
и  , а также координаты направляющего вектора a и b удовлетворяют условию
, а также координаты направляющего вектора a и b удовлетворяют условию 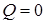 , или, как следует из (4*):
, или, как следует из (4*):
 .(4)
.(4)
Пусть  ‑ произвольная точка касательной. Тогда вектор
‑ произвольная точка касательной. Тогда вектор  коллинеарен ее направляющему вектору, поэтому
коллинеарен ее направляющему вектору, поэтому  . Отсюда вытекает:
. Отсюда вытекает:  . Преобразуем полученное выражение:
. Преобразуем полученное выражение:

точка  принадлежит кривой, поэтому:
принадлежит кривой, поэтому:  . Таким образом, уравнение касательной примет вид:
. Таким образом, уравнение касательной примет вид:  , т.е. (3). Полученное уравнение является уравнением прямой, так как коэффициенты при х и у отличны от нуля, в силу того, что точка
, т.е. (3). Полученное уравнение является уравнением прямой, так как коэффициенты при х и у отличны от нуля, в силу того, что точка  ‑ обыкновенная. Теорема доказана.
‑ обыкновенная. Теорема доказана.
Найдем уравнения касательных к эллипсу, гиперболе и параболе. Пусть  - точка эллипса, определенного своим каноническим уравнением:
- точка эллипса, определенного своим каноническим уравнением:  . Для этого уравнения
. Для этого уравнения  Из (19.14) получим:
Из (19.14) получим:  . Аналогично доказывается, что уравнение касательной в точке
. Аналогично доказывается, что уравнение касательной в точке  гиперболы, заданной своим каноническим уравнением, можно представить как
гиперболы, заданной своим каноническим уравнением, можно представить как  . В случае параболы
. В случае параболы  уравнение такой же касательной имеет с вид:
уравнение такой же касательной имеет с вид:
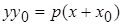 . (5)
. (5)
Касательные к кривым второго порядка обладают интересными геометрическими свойствами. Установим одно из них ‑ оптическое свойство параболы.
Пусть  - точка параболы, F - ее фокус. Доказать, что касательная к параболе в точке
- точка параболы, F - ее фокус. Доказать, что касательная к параболе в точке  образует равные углы как с прямой
образует равные углы как с прямой  , так и с прямой, проходящей через
, так и с прямой, проходящей через  и параллельной оси параболы.
и параллельной оси параболы.
 Решение. Будем считать, что данная парабола имеет каноническое уравнение
Решение. Будем считать, что данная парабола имеет каноническое уравнение 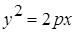 , координаты точки
, координаты точки  равны
равны  (рис. 1). В этом случае фокус F имеет координаты:
(рис. 1). В этом случае фокус F имеет координаты:  . Составим уравнение прямой
. Составим уравнение прямой  :
:  , или
, или  . Обозначим через m прямую, проходящую через
. Обозначим через m прямую, проходящую через  и параллельную оси параболы. Для параболы, заданной каноническим уравнением, ее ось совпадает с осью абсцисс, поэтому
и параллельную оси параболы. Для параболы, заданной каноническим уравнением, ее ось совпадает с осью абсцисс, поэтому  . Пусть l ‑ касательная к параболе в точке
. Пусть l ‑ касательная к параболе в точке  . Ее уравнение имеет вид (5). Найдем косинусы углов
. Ее уравнение имеет вид (5). Найдем косинусы углов  и
и  между прямыми l и
между прямыми l и  , l и m:
, l и m:
 ,
,  .
.
Углы  и
и 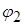 лежат в первой четверти, поэтому для доказательства их равенства достаточно проверить, что их косинусы равны. Преобразуем
лежат в первой четверти, поэтому для доказательства их равенства достаточно проверить, что их косинусы равны. Преобразуем  , учитывая при этом, что
, учитывая при этом, что  :
:
 .
.
Таким образом,  .Утверждение доказано.
.Утверждение доказано.
Оптическое свойство параболы широко используется при изготовлении осветительных приборов (прожекторов, фар автомобиля и т.д.). Отражательная поверхность таких устройств делается в виде параболического зеркала, а источник света помещают в его фокус. Тогда отраженные лучи образуют концентрированный световой пучок, направленный вдоль оси параболы. Эллипс и гипербола также обладают интересными оптическими свойствами. Например, если источник света поместить в фокусе эллиптического зеркала, то отраженные лучи будут проходить через второй его фокус.
Поиск по сайту: