 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Устойчивость сжатых стержней
Глава 7
§1 Общие положения. Критическая нагрузка. Формула Эйлера.
 |
Под устойчивостью понимается способность элементов конструкции сохранять первоначальную форму упругого равновесия при снятии внешней нагрузки. В теории устойчивости различают три формы упругого равновесия: устойчивое, при котором внешняя нагрузка не приводит к потере устойчивости; критическое равновесие, при котором изменение внешней нагрузки может привести либо к потере устойчивости, либо к сохранению устойчивого равновесия; неустойчивое, при котором внешняя нагрузка больше критической, что вызывает потерю устойчивости (рис.7.1).
Для оценки устойчивости конструкций необходимо установить величину критической нагрузки, для этого необходимо знать или учесть материал конструкции, его размеры, условие закрепления и эксплуатации, тогда расчет на устойчивость сжатых стержней, подвергающихся деформации продольного изгиба, т.е. изгиба, вызванного продольной нагрузкой, имеет следующий вид:
где [ Fy ] – допускаемая нагрузка на устойчивость, которая находится как нагрузка критическая;
ny – коэффициент запаса прочности.
Задачу по нахождению критической нагрузки впервые решил Леонард Эйлер, при этом он принял следующее допущение
Критическое напряжение, возникающее в стержне не должно превышать предела пропорциональности материала стержня.
Рассмотрим следующую расчетную схему нагружения стержня (рис.7.2).
ДУУЛБ:
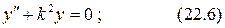
Для решения дифференциального уравнения (22.6) принимаем следующую зависимость
A и B – некоторые коэффициенты.
Решая совместно (22.9) и (22.7) получим формулу критической нагрузки
где принимается минимальный момент инерции сечения стержня I min, т.к. потеря его устойчивости будет происходить в плоскости наименьшей жесткости.
n – безразмерный параметр, характеризующий число или количество полуволн синусоиды по форме которой выпучивается сжатый стержень.
 |
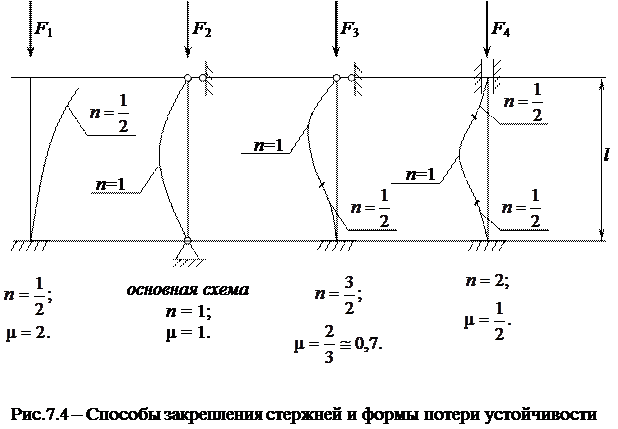В дальнейшем будем рассматривать случай, когда n =1, тогда F кр → min.
Безразмерный коэффициент n учитывает способ закрепления стержней, т.е. обуславливает форму потери устойчивости в зависимости от числа полуволн синусоиды.
Чем больше образуется полуволн синусосиды (n), тем большую силу выдерживает сжатый стержень без потери устойчивости. Для удобства расчетов формулу Эйлера принято записывать, используя преобразование, предложенное Ф.С. Ясинским.
где 
– коэффициент приведения длины, позволяющий заменить любую схему закрепления стержня основной схемой, когда n = 1.
Тогда μ l = l прив – приведенная длина стержня.
Таким образом, чем меньше коэффициент приведения длины стержня, тем большей устойчивостью он обладает.
§2 Пределы применимости формулы Эйлера.
На основании принятого допущения
Установим пределы применимости формулы Эйлера-Ясинского. Для этого получим зависимость критических напряжений, используя зависимость (22.11).
где 
– расчетная гибкость стержня, зависящая от размеров, формы и способа закрепления стержня (величина безразмерная).
Увеличение гибкости стержня приводит к понижению его устойчивости.
Рассмотрим совместно (23.2) и (23.1). Получим следующее
где 
– предельная гибкость стержня, зависящая только от физико-механических характеристик материала.
например:
| λпред | |
| чугун | |
| сталь | |
| дерево | > 110 |
Таким образом, согласно (23.3) формула Эйлера применима только для стержней, у которых расчетная гибкость больше или равна предельной гибкости.
Стержни, для которых выполняется условие (23.3’) называются стержнями большой гибкости (С.Б.Г.) – 
.
Стержни средней гибкости (С.С.Г.) подчиняются следующему условию
Для них критические напряжения определяются по эмпирическим зависимостям вида
– Формула Ясинского-Тетмайера
где a, b, c – экспериментальные коэффициенты, зависящие от типа материала.
Например: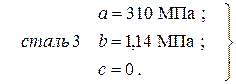 
Стержни малой гибкости (С.М.Г.) характеризуются следующим неравенством
где λ0 – расчетная гибкость, при которой раньше происходит потеря прочности, чем потеря устойчивости.
Стержни малой гибкости подвергаются расчету только на прочность по напряжениям предела текучести
 |
Все вышеизложенное можно изобразить следующим графиком зависимости критических напряжений от расчетной гибкости на рис.7.5 (на примере стали).
§3 Практические расчеты на устойчивость
В настоящее время расчет на устойчивость производится по следующему условию с применением так называемого коэффициента продольного изгиба φ.
где Aбрутто – площадь сечения сжатого стержня без учета ослаблений, т.к. потеря устойчивости стержня будет происходить по всей длине независимо от имеющихся ослаблений.
φ – коэффициент продольного изгиба, показывающий насколько необходимо уменьшить допускаемое напряжение в зависимости от материала и расчетной гибкости стержня (приводится в специальных таблицах).
По условию устойчивости (23.9) можно выполнить все виды расчетов – проверочный, проектировочный и расчет максимальной грузоподъемности.
Рассмотрим более подробно проектировочный расчет, который выполняется методом повторных приближений или методом «тыка»:
При проектировании стержней, работающих на устойчивость рекомендуется учитывать следующее:
1. Для стержней большой гибкости нет необходимости использовать высокопрочные стали, т.к. возникающие в них критические напряжения не зависят от показателей прочности, а обуславливаются только модулем упругости первого рода (λ > λпред).
2. Для стержней средней и малой гибкости целесообразно использовать высокопрочные материалы, т.к. для них критические напряжения зависят в большей степени от показателей прочности материала.
Поиск по сайту: