Неделя 4. Лекция 5.3.2015

Вид формулы интегрирования по частям для опред. интеграла.

Особенности замены переменной в определённом интеграле (пересчёт пределов интегрирования, не возвращаться к старой переменной). Пример.. = 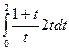изменение интервала при замене.

Приложения определённых интегралов.

Вычисление площадей. Найти площадь фигуры, ограниченной линиями

+ = .

Вычисление объёмов тел вращения. Вывод формулы 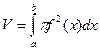, (ДОК)

Пример: доказательство этим методом формулы объёма шара.

Пример. Найти V получающийся при вращении кривой , . Отв. .

Длина дуги кривой. Вывод формулы для явно заданной кривой . (ДОК)

Пример. Длина кривой .

Для параметрически заданной в плоскости и пространстве:

. .

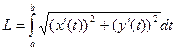Длина кривой в полярной системе координат: .

§5. Несобственный интеграл. Вводные примеры: , .

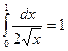Определения несобственных интегралов 1-го (неограниченная D(f)) и 2-го рода (неограниченная E(f)). Сходимость, расходимость.

ДОК, что несоб. интеграл 1-го рода сходится при , а интеграл 2-го рода при .

Примеры: , , .

Неделя 5. Лекция 12.3.2015 Несобственный интеграл.

Теорема 1. сходится первообразная имеет конечный предел .

Следствие. сходится .

Теорема 2. Признак сравнения в конечной форме. Если 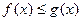и сходится интеграл , то сходится и интеграл . Пример.

Теорема 3. Признак сравнения в предельной форме. Если 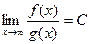, причём константа C отлична от 0 и от 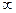, то интеграл сходится тогда и только тогда, когда сходится .

Пример.

Определение абсолютной сходимости. Из абсолютной сх-сти следует обычная (доказывается по признаку сравнения).

§6. Кратные интегралы. Определение. Геометрический и физический смысл.

Кратные интегралы, двойные, тройные. Свойства. Вычисление двойных интегралов по прямоугольной и непрямоугольной области. Геометрический смысл. Объём под поверхностью.

Сведение к повторным: интегрирование величин всех площадей криволинейных трапеций в сечениях по перпендикулярному направлению.

Аналогично, массив в программировании может быть не прямоугольным, тогда во внутреннем цикле двойного цикла границы переменные и зависят от переменной, определённой во внешнем цикле:

for i: = 1 to 10 do for j: = 1 to i do read (a[i,j]); end; end;

Примеры: (1/4) (1/8)

Смена порядка интегрирования: Пример: =

= =

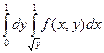
Вычисление тройных интегралов. Примеры. Вычислить (1/8)

При f = 1 площадь (если двойной) или объём (если тройной) интеграл.

Неделя 6. Лекция 19.3.2015 Кратные интегралы

Пример. Найти объём тетраэдра с вершинами (0,0,0), (1,0,0), (1,1,0), (1,1,1). (1/6)

Приложения кратных интегралов. Площадь поверхности.

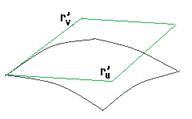
Площадь параллелограмма вычисляется с помощью векторного произведения векторов (1,0,f ‘_x), (0,1,f ‘_y).

Формула площади явно заданной поверхности: .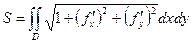

Замена переменных в кратных интегралах. Полярные координаты на плоскости:

. Определитель Якоби: .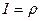

При замене двух старых на две новые переменные в плоскости, существует уже 4 различных частных производных, и из них можно образовать матрицу 2-го порядка.

= Определитель: = .

Геометрический смысл определителя Якоби - правильный учёт искажений (деформаций).

Чертёж - слева в плоскости параметров , справа в плоскости .

множитель, появляющийся при замене переменной в неопределённом или определённом интеграле. Так, если , то при замене пишем . Множитель фактически и является одномерным якобианом, но только для матрицы порядка 1 определитель вычислять было не нужно, так как он совпадает с самим этим элементом.

Пример: Вычислить интеграл где D - часть круга единичного радиуса в первой четверти плоскости. Решение. = = =

= = =

= = = .

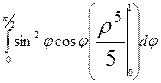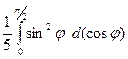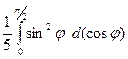Пример: Доказать формулу площади круга с помощью полярных координат.

Решение. = = = = = .

Цилиндрические и сферические координаты в пространстве.

Существует два различных обобщения полярных координат для трёхмерного пространства.

и .

Определитель Якоб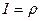и и соответственно.

Криволинейные интегралы от векторной функции. Определение. Свойства, геометрический и физический смысл. Работа силы по перемещению точки по кривой.

Пример. Вычислить работу поля F = (xy, x+y) по участку параболы от (0,0) до (1,1).

Неделя 7. Лекция 26.3.2015 ГЛАВА 2. Дифференциальные уравнения

§ 1. Дифференциальные уравнения 1-го порядка.

1) Уравнения с разделяющимися переменными. Примеры: , ,

2) Однородные (по степени) уравнения . Доказать, что замена сводит однородное уравнение к уравнению с разделяющимися переменными.

3) Линейные уравнения. Вид , либо .

Однородные (с помощью разделения переменных). Примеры ,

Неоднородные: Метод Лагранжа для неоднородных линейных уравнений 1 порядка. Обоснование метода.

Неделя 8. Лекция 2.4.2015 Пример.

4) Уравнения Бернулли. Обосновать метод сведения уравнения Бернулли к линейному уравнению с помощью замены.

5) Уравнения в полных дифференциалах, кратко.

Условия Коши и их применение.

§ 2. Дифференциальные уравнения n-го порядка.

Методы понижения порядка.

Случай 1) если в уравнении не содержатся младшие порядки производных, то есть тип уравнения то замена y^(k)=z, при этом y^(k+1)=z’,...

Доказать, что замена понижает порядок уравнения .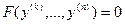

Пример. Варианты начальных условий:

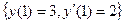(условия Коши) или (в двух различных точках)

Случай 2) если в уравнении содержатся все порядки производных, но нет х, то есть тип уравнения то замена y’=p(y)

Вывести и обосновать замену, доказать что 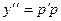. Доказать, что замена понижает порядок уравнения, в котором отсутствует , то есть уравнения вида .

Пример: 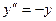(уравнение колебаний) решить этим методом.

Неделя 9. Лекция 9.4.2015 Дифф.уравнения - линейные неоднородные.

Линейное уравнение высшего порядка.

- неоднородное.

- однородное.

Теорема 1. Доказать, что 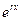является решением r есть характеристический корень

Пример .

Теорема 2. Линейная комбинация решений линейного однородного дифференциального уравнения тоже является его решением.

Линейные однородные. Примеры.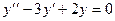

Неделя 10. Лекция 16.4.2015 Вероятность: комбинаторика.

Неделя 11. Лекция 23.4.2015 Вероятность: формула полной вероятности, формула Байеса

Неделя 12. Лекция 30.4.2015 Вероятность: схема Бернулли, теоремы Муавра-Лапласа, поток Пуассона.

Неделя 14. Лекция 14.5.2015 Вероятность: случайные величины, мат. ожидание, дисперсия.

Неделя 15. Лекция 21.5.2015 Вероятность: корреляция

Неделя 16. Лекция 28.5.2015 Вероятность: элементы статистики.

Неделя 17. Лекция 4.6.2015 Об ошибках в контрольных, подготовка к сессии, обзорная лекция.

Поиск по сайту: