А.С.Орлов, В.А.Георгиев, Н.Г.Георгиева, Т.А.Сивохина

Крутящий момент при сматывании ролико-барабанной моталкой складывается из моментов сил натяжения, изгиба листа и трения в опорах:

.

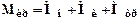Момент натяжения полосы:

,

где k_н – коэффициент натяжения. Равен 0,5÷0,8 для h = 0,3÷1мм; 0,2÷0,5 для h = 1÷2мм; 0,1÷0,2 для h = 2÷4мм;

D_p – диаметр рулона.

Момент изгиба учитывается только при толщине полос > 3мм:

.

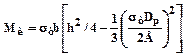Момент трения в подшипниках:

,

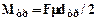где F – результирующая сила на барабане от действия натяжения и сил веса барабана и рулона:

,

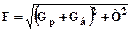где Т – величина натяжения;

G_р, G_б – вес рулона и барабана соответственно.

Для определения динамического момента моталки нужно рассчитать моменты инерции вращающихся масс. Приведенный к валу двигателя момент инерции механизма:

,

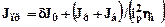где δ – коэффициент, учитывающий инерцию вращающихся деталей редуктора; δ = 1,1÷1,4;

J₀ – момент инерции якоря двигателя; J_р, J_б – моменты инерции рулона и барабана соответственно:

,

где m_р, m_б – массы рулона и барабана соответственно.

i_p – передаточное число редуктора;

η_м – к.п.д. передачи моталки.

Динамический момент электродвигателя в период пуска:

,

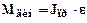где ε – угловое ускорение привода. Для безредукторного привода:

,

где а – ускорение полосы при смотке; а = 0,75÷1,5м/с².

Максимальный момент двигателя при пуске:

,

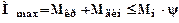где М_н – номинальный момент двигателя;

ψ – кратность пускового момента электродвигателя.

Величина натяжения при начале сматывания:

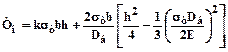
Величина натяжения при начале сматывания:

Мощность в начале и в конце сматывания равна:

;

,

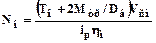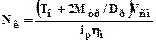где V_см – скорость смотки.

Расчетная мощность двигателя моталки:

.

Лекция № 16

16.1 Динамические расчеты оборудования прокатных цехов

При работе машин прокатных цехов во многих случаях возникают значительные силы инерции, которые существенно влияют на их прочность и надежность. Пренебрежение динамическими нагрузками, особенно при расчетах приводов, влечет за собой ошибки в определении реальных нагрузок и, как следствие, выход машин из строя при вроде бы нормальных условиях работы. Аварии возникают при небольших статических нагрузках в результате усталостного разрушения деталей от действия переменных нагрузок. Практически 90% разрушений деталей металлургических машин носят усталостный характер. Причем во многих случаях из-за не учета динамических нагрузок, которые обычно являются переменными.

Кроме того, динамические нагрузки могут усложнить или даже нарушить нормальный ход технологического процесса. Например, возникновение крутильных колебаний в линии главных приводов ведет к невозможности отработки двигателями заданных скоростных режимов.

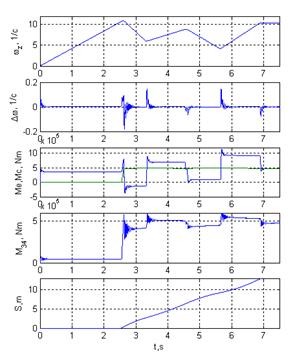
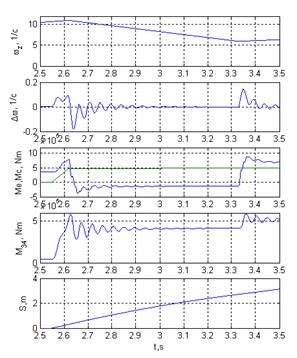
Независимо от назначения и конструктивных особенностей все машины обладают общими свойствами - упругостью звеньев и способностью при определенных условиях к возбуждению в них колебательных процессов. Под действием внешних нагрузок (моментов и сил двигателей, технологических сопротивлений) упругие элементы деформируются, а движущиеся массы машин совершают, кроме основного вращательного движения, крутильные или продольные колебания. Кроме того, при наличии зазоров в сопряжениях деталей, возникают ударные нагрузки, которые генерируют упругие колебаниях в деталях. В результате линия приводов нагружается дополнительными моментами или силами упругости, изменяющимися во времени с частотой собственных колебаний системы. На рис. 16.1 показан характер изменения моментов в главной линии ТЛС с групповым приводом (на рис. б) - в большем масштабе). Видно, что при изменении скорости в проходе возникают колебательные процессы в шпинделях, которые ведут к колебательному характеру отработки скорости.

Расчет динамических нагрузок колебательного характера в машинах включает:

1. Составление физической модели машины;

2. Определение величины и характера изменения внешних нагрузок, приложенных к системе (машине);

3. Составление дифференциальных уравнений движения системы с учетом упругих свойств ее звеньев;

4. Определение частот собственных колебаний звеньев и всей системы;

5. Расчет упругих сил и моментов в звеньях системы и действительных перемещений и скоростей рабочих органов машины.

Привод любой машины состоит из большого числа сосредоточенных и распределенных масс, из-за чего теоретический расчет такой системы является затруднительным. Поэтому действительную систему заменяют простой приведенной расчетной схемой с небольшим числом масс, но обеспечивающей необходимую точность расчета. Например, групповой привод чистовой клети ТЛС (рис.16.2) заменяется расчетной схемой (рис.16.3). В ней механические инерции отдельных частей, выраженные через моменты инерции j_i, изображены прямоугольниками, площади которых пропорциональны этим инерцииям.

a)	б)

Рисунок 16.1 – Графики переходных процессов при прокатке на ТЛС с изменяющейся скоростью

Рисунок 16.2 – Главная линия чистовой клети толстолистового стана

Рисунок 16.3 – Расчетная схема привода чистовой клети

Кинематические связи между инерциями (вращающимися массами) изображены упруго-диссипативными элементами в виде параллельного соединения коэффициентов жесткости (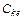) и рассеяния (диссипации – 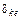). Первые определяются отношением упругих моментов в таких элементах к их деформации, а вторые – уровнем потерь

в них при наличии скорости деформации.

16.2 Составление физической модели машины

Составление физической модели является одним из наиболее ответственных этапов динамических исследований. Обоснованный переход от реальной машины к эквивалентной расчетной схеме и точность определения параметров этой схемы определяют достоверность получаемых результатов.

Основными параметрами линий привода различных машин являются моменты инерции их масс и жесткости отдельных звеньев. Моменты инерции вращающихся масс:

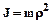[кг·м²].

В старых справочниках вместо моментов инерции приводятся маховые массы GD². Переход от технической системы единиц к системе SI осуществляется по соотношению:

.

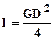Жесткостью называется коэффициент, который определяет упругую деформацию при заданном силовом факторе.

При растяжении стержня жесткость равна:

[Н/м].

По закону Гука удлинение стержня:

.

Отсюда:

.

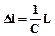Параметр, обратный жесткости, называется податливостью:

[м/Н].

Жесткость пружины растяжения или сжатия:

,

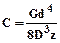где G - модуль упругости при сдвиге;

d - диаметр проволоки;

D - средний диаметр пружины;

z - число рабочих витков пружины.

Поперечная жесткость балок (валов у машин) зависит от способа их крепления. Жесткость консольной балки:

,

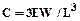где W - экваториальный момент инерции сечения балки, м⁴.

Особый интерес при расчете приводов представляет крутильная жесткость. В этом случае коэффициент С - это крутящий момент М_кр, закручивающий вал на угол θ = 1рад.:

.

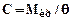Жесткость круглого вала:

,

где I_p - полярный момент инерции сечения вала с круглой формой:

,

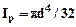L - длина закручиваемого участка вала.

При последовательном соединении звеньев упругой системы общая эквивалентная податливость равна сумме податливостей всех звеньев:

.

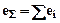При параллельном соединении проще определять общую жесткость, которая равна сумме жесткостей всех звеньев:

.

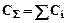При параллельно-последовательном соединении трех звеньев:

.

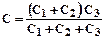
При наличии в приводе зубчатых передач (редукторов) жесткости приводятся к одну из валов. Обычно к валу двигателя или рабочей машины, аналогично приведению масс или моментов инерции:

,

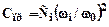где С_i - жесткость соответствующих линий передач, вращающихся с угловой скоростью ω_i;

ω₀ - угловая скорость вала, к которому приводится система.

Приведение моментов инерции масс с учетом к.п.д. передачи осуществляется по соотношению:

.

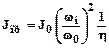16.3 Динамические нагрузки в машинах

Самой простой динамической моделью любой машины является т.н. двухмассовая эквивалентная схема (рис.16.4), в которой J₁ - момент инерции первой массы привода; J₂ - момент инерции второй массы механизма, приведенный к валу двигателя; С₁₂ - приведенная жесткость линии передач привода; τ - время; θ₁, θ₂ - угловые перемещения масс, рад.

Рисунок 16.4 - Схема двухмассовой системы механизма

На рис.16.4 - М₁ - момент двигателя; М₂ - момент технологического сопротивления рабочей машины, приведенный к валу двигателя со знаком минус).

Для двухмассовой системы уравнения движения в переходной период имеют вид:

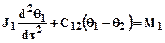(16.1)

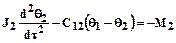(16.2)

В уравнениях 16.1..16.2 первые слагаемые - моменты сил инерции соответствующих масс; вторые - моменты сил упругости в связях привода; правые части - моменты внешних сил (двигателя и технологического сопротивления в рабочем звене машины).

Характер динамических процессов и величины амплитуд колеба-

ний зависят от параметров системы, закона нагружения привода сила-

силами технологического сопротивления М₂ и действия двигателя М₁. Решение системы уравнений, которое и дает графики изменения моментов и скоростей во времени, в настоящее время осуществляется моделированием среде Simulink пакета MATLAB.

16.4 Динамические нагрузки от ударов в зазорах

Обычно в приводах машин прокатных цехов имеются большие зазоры в соединениях (в зубчатых муфтах и передачах, универсальных шпинделях и т.д.). В период неустановившегося движения в момент упругого замыкания зазоров в приводных линиях возникают ударные нагрузки, вызывающие колебательные процессы.

Ударные нагрузки увеличивают напряжения в деталях сверх полученных расчетами на статическую прочность. Это увеличение учитывается коэффициентом динамичности К_д. Для двухмассовой системы он может определятся по выражению:

,

где n₂ = J₁/(J₁+J₂);

τ_в - продолжительность действия внешних сил.

Уменьшения динамических нагрузок от ударов при выборе зазоров достигается качественным изготовлением деталей и монтажом механизмов, применением специальных устройств для уменьшения или исключения зазоров, введением предпусковых ступеней сопротивления в цепях управления электродвигателями, снижающих скорость выбора зазоров.

16.5 Уменьшение динамических нагрузок

Снижение динамических нагрузок в машинах прокатных цехов является весьма актуальной задачей вследствие их уникальности и большой стоимости. Решение этой задачи осуществляется целым комплексом мероприятий. Главными из них являются:

1. Выбор рациональных кинематических схем механизмов без пассивных связей;

2. Определение действительных физических процессов, происходящих в машинах с учетом жесткости деталей, зазоров в соединениях, характеристик двигателей в различных режимах эксплуатации;

3. Определение оптимальных кинематических и динамических параметров машин на стадии проектирования путем математического моделирования;

4. Улучшение динамических характеристик машин посредством расчета оптимальных соотношений распределения масс жесткостей системы, обеспечивающих минимальные динамические нагрузки и их быстрое затухание;

5. Повышение качества материалов и технологии изготовления деталей машин, точности обработки и монтажа машин, уменьшение зазоров в соединениях;

6. Создание конструкций с рациональным расположением приводов без длинных и сложных трансмиссий; применение индивидуальных приводов, установка в тяжелых машинах многодвигательных приводов, а также безредукторных и гидравлических приводов, обладающих лучшими динамическими свойствами;

7. Введение демпфирующих устройств, поглощающих энергию колебаний - упруго-демпфирующих муфт с нелинейными характеристиками, гидравлических амортизаторов с дискретно-меняющимися характеристиками;

8. Создание специальных устройств для выбора зазоров в соеди-

нениях; применение уравновешивающих устройств в механизмах циклического действия.

Применение всех этих способов не исключает опасных перегрузок при возникновении случайных нагрузок, не поддающихся теоретическому расчету. Поэтому в машинах устанавливаются механические защитные устройства от аварийных поломок машин.

А.С.Орлов, В.А.Георгиев, Н.Г.Георгиева, Т.А.Сивохина

Поиск по сайту: