АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Инкремент. Запрет импликации по A. Инверсия импликации от B к A

Читайте также:
  1. А. Инверсия
  2. Г. – очередной запрет на издание и хранение украинско-язычной литературы.
  3. Г. – цензурой был введен запрет на такие слова, как «казак», «московит», «Украина», «украинский» и прочее, что имело отношение к украинскому национал-символическому содержанию.
  4. Глава 3. Транспортная задача с запретами
  5. Движение за запрет опиума. Патриотическая деятельность Линь Цзэсюя
  6. Запрет индексирования некоторых страниц (файл robots.txt)
  7. Запрет на открытие филиалов.
  8. Запрет на привлечение субподрядчиков для выполнения работ и оказания услуг.
  9. Запретный плод
  10. Запреты для судоводителей маломерных судов
  11. Запреты, связанные с гражданской службой
  12. Инверсия доминирования, доминирование и циклы формулы любви
     
     
     
     

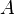
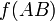
Мнемоническое правило для инверсии импликации от B к A звучит так: На выходе будет:

  • «1» тогда и только тогда, когда на «B» больше «A»,
  • «0» тогда и только тогда, когда на «B» меньше либо равно «A»

Примечание 1. Элементы импликаций не имеют промышленных аналогов для функций с количеством входов, не равным 2.
Примечание 2. Элементы импликаций не имеют промышленных аналогов.

Этими простейшими логическими операциями (функциями), и даже некоторыми их подмножествами, можно выразить любые другие логические операции. Такой набор простейших функций называется функционально полным логическим базисом. Таких базисов 4:

  • И, НЕ (2 элемента)
  • ИЛИ, НЕ (2 элемента)
  • И-НЕ (1 элемент)
  • ИЛИ-НЕ (1 элемент).

Для преобразования логических функций в один из названых базисов необходимо применять Закон (правило) де-Моргана.


1 | 2 | 3 | 4 | 5 | 6 | 7 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)