Література..........................................................................................94

„Луганський національний університет

імені Тараса Шевченка”

вул. Оборонна, 2 м. Луганськ, 91011. Т/ф (0642) 58-03-20.

e-mail: alma-mater@list.ru

Свідоцтво суб’єкта видавничої справи ДК № 3459 від 09.04.2009 р.

ЗМІСТ

Вступ…….......................................................................................5

1 Моделі і моделювання

1.1 Загальні відомості про моделі і моделювання…………….…………….6

1.2 Співвідношення між моделлю і оригіналом……………………………..6

1.3 Класифікація моделей і моделювання………………………… ……….7

1.4 Комп’ютерна модель і її переваги……………….……………………......8

1.5 Етапи створення комп'ютерної моделі…………………..………………10

2 Моделювання технічних систем на основі теорії подібності

2.1. Поняття подібності………………..…………………………………….15

2.2. Види подібності….……………………………………………………...17

2.3. Критерії подібності.………………………………………………….…18

2.4. Теореми подібності……………………………………………………..21

2.5. Аналіз розмірностей……….…………………………………………...22

3 Математичні моделі

3.1. Загальна характеристика математичної моделі…………….………..28

3.2. Класифікація математичних моделей…………………………………31

3.3. Побудова і аналіз математичних моделей……………..…………...…34

3.4. Компонентні і топологічні рівняння модельованого об’єкту……….36

4 Математичні схеми моделювання систем

4.1 Безперервно-детерміновані моделі (D-схеми)……………….................38

4.2 Безперервно-стохастичні моделі (Q-схеми)……………….....................40

4.3 Дискретно-детерміновані моделі (F-схеми)……………….............……42

4.4 Дискретно-стохастичніні моделі (P-схеми)……………….......….…….46

5 Математична модель електричного ланцюга

5.1 Компонентні і топологічні рівняння електричного ланцюга …….......48

5.2 Матриця головних перетинів і її властивості..........................................50

5.3 Матриця головних перетинів довільної схеми ………………...............52

5.4 Формування матриці головних перетинів ……………………………...54

5.5 Вектор стану електричного ланцюга …………………………………...58

5.6 Математична модель лінійного електричного ланцюга ………………59

5.7 Матричні коефіцієнти рівнянь математичної моделі електричного ланцюга.............................................................................................................62

5.8 Математична модель електричного ланцюга з нелінійними

елементами ……………………………………………………………………65

5.9 Підготовка даних по електричній моделі для введення в ЕОМ ………68

6 Імовірнісне моделювання

6.1 Метод статистичних випробувань…………………………………….....73

6.2 Генератори випадкових чисел……………...............................................74

6.3 Моделювання випадкових подій та дискретних величин…...................80

6.4 Модедювання безперервних випадкових величин…..............................83

6.5 Моделювання випадкових процесів………………..…............................86

7 Прийняття рішень за результатами моделювання

7.1 Відображення результатів моделювання…………………………….....88

7.2 Методи прийняття рішень………………….............................................90

7.3 Прийняття рішень щодо удосконалення систем….…………................91

Література..........................................................................................94

ВСТУП

Моделювання як одну з найважливіших категорій процесу пізнання неможливо відокремити від розвитку людства. Ще з дитинства людина пізнає світ, спочатку через іграшки та ігри, і відображає, або моделює, дійсність. З роками людина використовує більш складні моделі, що дають можливість “програвати” будь-які життєві та виробничі ситуації й отримувати такі рішення, що дозволяють знайти найкращий спосіб вирішення проблеми.

Методи комп’ютерного моделювання широко застосовуються в усіх сферах діяльності людини – від конструювання моделей технічних, технологічних та організаційних систем до вирішення проблем розвитку людства та всесвіту. Класичними об’єктами моделювання є інформаційні, виробничі, транспортні та інші системи, які в більшості випадків застосовуються для розв’язання задач проектування, реконструкції та довгострокового планування, а також використання моделей у контурі керування, тобто в реальному масштабі часу.

1 Моделі і моделювання

1.1 Загальні відомості про моделі і моделювання

Модель - це спрощене представлення досліджуваного об'єкту (системи). Вона повинна відображати найбільш істотні (з погляду мети дослідження) властивості об'єкту, що вивчається. Об'єкт, для якого створюється модель, прийнято називати оригіналом. Не завжди є можливість або доцільність досліджувати безпосередньо оригінал. Часто дослідження проводять на моделі оригінала, а потім результати дослідження переносять на оригінал. Залежно від мети дослідження для одного і того ж оригіналу може бути створено декілька моделей.

Моделювання - це процес створення моделі, її дослідження і обробка отриманих результатів. Найчастіше моделюванням займаються при аналізі існуючих об'єктів (систем) або в процесі проектування таких об'єктів (систем).

Строго кажучи, моделюванням людство займається з давніх часів. Ще з дитинства чоловік пізнає мир, спочатку через іграшки і гру, і відображає, або моделює, дійсність. З роками людина використовує складніші моделі, що відображають складнішій ситуації. Моделювання дозволяє аналізувати навіть ситуації, в яких реальний об'єкт не може функціонувати. Можна моделювати, наприклад, катастрофи, рідкісні випадки і навіть такі явища і процеси, яких не існує в реальності.

Зараз методи моделювання широко використовують у всіх сферах діяльності людини – від конструювання моделей технічних, технологічних і організаційних систем до рішення проблем розвитку людства і Всесвіту. Сьогодні найпотужніший в світі суппер-компьютер NEC Vector SX6 встановлений в центрі моделювання Землі в Йокагамі (Японія) і використовується для моделювання основних властивостей кліматичної системи Землі.

1.2 Співвідношення між моделлю і оригіналом

Науковою основою моделювання є теорія подібності. Основним в цій теорії є поняття аналогії, тобто подібність об'єктів за деякими ознаками. Подібні об'єкти називаються аналогами.

Аналогія між об'єктами може встановлюватися по якісних, по кількісних ознаках або по тих і інших.

Основним видом кількісної аналогії є математична подібність. Об'єкти в цьому випадку описуються аналогічними рівняннями або функціями, що відрізняються тільки значеннями коефіцієнтів або констант.

Іншим видом кількісної аналогії можна вважати фізичну подібність. В цьому випадку об'єкти не можуть бути описані математично, і їх подібність визначається співвідношенням фізичних параметрів, які характеризують досліджуваний процес в оригіналі і на моделі.

Будь-яка модель відображає властивості оригіналу лише частково. І чим більше властивостей оригіналу відбито в моделі, тим ближче модель до оригіналу, тим вона точніша. Але одночасно з підвищенням точності моделі росте і її складність. Дослідникові постійно доводиться шукати компроміс між бажаною точністю моделі і її складністю.

На ступінь відповідності між об'єктом і моделлю указують два поняття: ізоморфізм і гомоморфізм.

Об'єкт і його модель ізоморфні, якщо існує взаємооднозначна відповідність між ними, завдяки якій можна перетворити одне уявлення на інше. Строго доведений ізоморфізм для об'єктів різної природи дає можливість переносити знання з однієї області в іншу. Приклади ізоморфізмів: оригінал і його фото; оригінальний текст і його переклад на другу мову; електричні процеси в сердці і електрокардіограма цих процесів і т. п.

Проте існують і менш тісні зв'язки між об'єктом і моделлю. Це так звані гомоморфні зв'язки. Вони встановлюють однозначну відповідність тільки в один бік - від моделі до об'єкту. Приклад гомоморфізму: любі знання здобуті з електрокардіограми переносяться на відповідне сердце, але не все, що відбувається в сердці, відображається на електрокардіограмі.

1.3 Класифікація моделей і моделювання

Моделі умовно можна розбити на дві групи - матеріальні моделі і ідеальні. Першій групі відповідає предметне моделювання, а другий абстрактне.

Основними різновидами предметного моделювання є фізичне і аналогове моделювання. Фізичним прийнято називати моделювання, при якому реальний об'єкт замінюється його збільшеною або зменшеною копією. Копія зберігає геометричні пропорції і фізичні принципи дії.

Аналогове моделювання засноване на заміні початкового об'єкту об'єктом іншої фізичної природи (об'єктом - аналогом). Поведінка аналога визначається аналогічними фізичними законами. Наприклад, коливання і резонанс в механічних системах аналогічні коливанням і резонансу в електричних ланцюгах.

Ідеальні моделі - це абстрактні образи об'єктів, що заміщуються. Розрізняють два типи ідеального моделювання: інтуїтивне і знакове. Інтуїтивне моделювання використовується людиною і іншими живими істотами для віддзеркалення навколишнього світу і прогнозу його реакцій. Який механізм інтуїтивного моделювання – не відомо.

Знакове моделювання допускає використання в якості моделі знаків або символів: схем, графіків, мереж, креслень і т. п. Найбільш важливим видом знакового моделювання є математичне моделювання.

Обов'язковим учасником знакового моделювання є інтерпретатор знакової моделі. Інтерпретатором, як правило, виступає людина, що розуміє сенс використовуваних знаків, проте вже існує безліч технічних пристроїв, що володіють схожими можливостями.

Залежно від того, змінюються властивості моделі в часі чи не змінюються, моделі діляться на динамічні і статичні.

Залежно від того, як відображаються стани моделі в часі, розрізняють дискретні, безперервні і дискретно – безперервні (гібридні) моделі.

Крім того, моделі діляться на детерміновані і стохастичні (імовірнісні).

1.4 Комп’ютерна модель і її переваги

Інформаційну модель, реалізовану на комп'ютері, називають комп'ютерною.

Комп'ютерні моделі дозволяють:

· спостерігати і досліджувати явища і процеси в динаміці їх розгортання;

· здійснювати багаторазові випробування моделі;

· отримувати різноманітні кількісні показники в числовому або графічному вигляді, зокрема такі, які вимагають виконання складних, багаторазових або трудомістких розрахунків.

За допомогою комп'ютерного моделювання вивчаються об'єкти і явища, які неможливо, дорого або небезпечно відтворювати в реальних умовах. Це дозволяє не тільки економити матеріальні ресурси, але і зберігати екологічні умови існування людини, уникати можливих шкідливих або руйнівних наслідків проведення натурних випробувань.

Комп'ютерне моделювання є унікальним інструментом пізнання швидкоплинні і, навпаки, надзвичайно повільних процесів. Їх можна досліджувати на комп'ютері, розтягуючи або стискаючи час або навіть зупиняючи його для вивчення певних фаз процесу. Моделювати і вивчати за допомогою комп'ютера можна і такі явища, які не відбувалися, і невідомо, чи відбудуться коли-небудь в реальному житті, - наприклад, зустріч нашої планети з іншим космічним об'єктом.

Комп'ютерне моделювання застосовується для вирішення множини наукових, технічних, економічних і інших проблем. Наприклад, для встановлення причин технічних і природних катастроф, дослідження біологічних і соціальних процесів, прогнозування зміни клімату на нашій планеті і т. п. Так, після того, як космічна станція «Мир» виробила свій ресурс, її необхідно було спустити на Землю, точніше приводнити. Завдання ускладнювалося тим, що 130-тонна станція при вході в атмосферу повинна була розпастися на тисячу уламків різної ваги. Достатньо великі з них могли пробити бетонну плиту в два метри завтовшки. За допомогою комп'ютерного моделювання був визначений той момент, коли станції потрібно дати імпульс для спуску в заданий район акваторії Тихого океану. Всім морським і повітряним судам, жителям навколишніх островів Того було послано попередження. Точність моделювання повністю підтвердилася: у запрограмований час станція увійшла до води в заданому районі. Після приводнювання станції газети писали про черговий тріумф науки.

Комп'ютерна модель володіє особливими властивостями в порівнянні з математичною моделлю. Вона не є просто записаною на іншій мові - мові комп'ютера математичною моделлю.

Комп'ютерна модель має дві складові – програмну і апаратну (рис.1.1).

Рис.1.1 Складові комп’ютерної моделі

Програмна складова (моделююча програма) є абстрактною знаковою моделлю спеціального вигляду, яка інтерпретується фізичним пристроєм – процесором комп'ютера і «виконується». В результаті ми спостерігаємо деякий фізичний процес, зокрема рух образів на екрані., які інтерпретуємо як поведінка моделі. Під комп'ютером в даному випадку досить розуміти будь-який пристрій, що складається з програмної і апаратної частин, здатне інтерпретувати і виконувати програми. Це може бути і суперкомп'ютер, і вбудований мікропроцесор з «зашитою» в його пам'ять програмою.

Сукупність комп'ютера і моделюючої програми є вже фізичним пристроєм і, таким чином, комп'ютерне моделювання можна вважати особливим видом фізичних моделей.

Існування таких особливих фізичних моделей на базі комп'ютерів дозволяє говорити ще про одну сторону комп'ютерного моделювання. З цієї точки зору комп'ютерне моделювання володіє унікальним набором привабливих властивостей, до яких, перш за все, відносяться майже необмежена складність моделей. Зручним також є розділення на «м'яку» частину (програмне забезпечення), яку необхідно змінити при переході до іншої моделі, і «жорстку» частину (апаратуру і операційну систему), яка залишається незмінною. Комп'ютерна модель, таким чином, в певних умовах може виступати як імітатор реального об'єкту. Слово «imitatio» (лат.) означає – наслідування, підробка. Її можна «підключати» до інших реальних об'єктів точно так, як її фізичні прототипи. Це властивість комп'ютерних моделей дозволяє використовувати їх у складі напівнатуральних моделей, зібраних з реальних пристроїв і імітаторів реальних пристроїв, які використовуються при створенні і випробуванні складних технологічних систем.

Слід зазначити, що комп'ютерні моделі можуть створюватися не обов'язково на основі математичних моделей. У їх основі можуть лежати записані на мові програмування уявлення про об'єкт, що існують в свідомості розробника (пунктирна лінія на рис. 1.2).

1.5 Етапи створення комп'ютерної моделі

Для створення комп'ютерної моделі застосовується певна технологія. За цією технологією процес моделювання розбивається на п'ять основних етапів. Кожен етап має певну мету, яка досягається шляхом виконання відповідних дій.

Основні етапи комп'ютерного моделювання.

Етап 1. Постановка задачі і її аналіз.

Етап 2. Побудова інформаційної моделі.

Етап 3. Розробка методу і алгоритму дослідження моделі.

Етап 4. Розробка комп'ютерної моделі.

Етап 5. Проведення комп'ютерного експерименту.

Рис.1.2 Варіанти створення комп’ютерних моделей

Розглянемо суть цих етапів на прикладі завдачі Робіна Гуда.

Робіну Гуду потрібно передати записку другу, якого ув'язнили у в'язницю замку Ноттінгем. Замок оточений високою стіною. Записку можна тільки закинути разом з каменем у вікно в'язниці, але кидати камінь потрібно так, щоб він пролетів крізь бійницю в стіні (рис.1.3).

Постановка задачі і її аналіз

Метою етапу є конкретизація і уточнення завдання моделювання. Для цього виконуються такі дії:

· з'ясовується, з якою метою створюється модель;

· уточнюється, які саме результати і в якому вигляді потрібно отримати;

· визначається, які дані потрібні для створення моделі;

· встановлюється, чи є обмеження на вхідні дані, тобто за яких умов можна отримати потрібні результати, а при яких - ні.

Рис.1.3 Задача Робіна Гуда

Для нашої задачі метою складання моделі є визначення, чи можна закинути камінь до в'язниці, а якщо так, то як повинен діяти Робін Гуд. Результатом моделювання повинна бути відповідь на поставлене питання і, якщо вона позитивна, - рекомендації для Робіна Гуда. Для побудови моделі потрібні дані про геометрію споруд (відстань стіни від замку, товщина стіни, висота і розміри бійниці, висота і розміри вікна в'язниці) і про Робіна Гуда - який у нього зріст, з якою найбільшою силою може кинути камінь. Що саме ми моделюватимемо? Траєкторію каменя на фоні споруд.

Побудова інформаційної моделі

Метою етапу є встановлення і опис взаємозалежностей між параметрами моделі. На цьому етапі:

· визначаються параметри моделі і знаходяться взаємозв'язки між ними;

· оцінюється, які з параметрів є впливовими і повинні бути враховані при побудові моделі, а якими можна нехтувати;

Такий аналіз здійснюється з урахуванням поставленого завдання і має на меті максимальне спрощення моделі. Разом з тим, це спрощення не може бути надмірним, щоб модель не втратила адекватність.

· вводиться система умовних позначень, і в цих позначеннях здійснюється опис залежностей між параметрами моделі. У результаті виходить знакова інформаційна модель.

Побудуємо інформаційну модель для нашої задачі. Геометричні параметри споруд позначимо, як показано на рис.1.3. Вважатимемо, що рух каменя відбувається в одній площині. Позначимо її XOY з початком координат в основі зовнішньої сторони стіни. Силу, з якою Робін Гуд кидає камінь, подамо через початкову швидкість каменя V₀. Кут до горизонту, під яким робиться кидок, позначимо через α. Нехтуватимемо опором повітря і залежністю прискорення вільного падіння g від висоти. Камінь вважатимемо матеріальною точкою, його траєкторію визначатимемо як залежність координат x, у від часу t.

Робін Гуд кидає камінь з висоти свого росту r, знаходячись на відстані l₁ від стіни. На траєкторію каменя впливають початкова швидкість каменя V₀ і кут α. Як відомо з фізики

Це і є математична модель нашої задачі.

Розробка методу і алгоритму дослідження моделі

Метою етапу є складання алгоритму дій для отримання потрібних результатів.

На цьому етапі:

. враховуючи інформаційну модель підбирається або розробляється метод отримання потрібних результатів;

. за вибраним методом складається детальний план рішення задачі, розробляється алгоритм отримання результатів.

Модель нашої задачі є простою, координати каменя обчислюються за формулами. Траєкторію каменя будуватимемо на тій же площині, де відображені і споруди. Виводи про результат кидання каменя визначатимемо візуально.

Розробка комп'ютерної моделі

Метою етапу є отримання комп'ютерної моделі, придатної для дослідження. Для цього здійснюються:

. вибирання засобів реалізації моделі на комп'ютері. Серед багатства існуючих засобів вибираємо найбільш зручні з урахуванням поставленої задачі і її інформаційной моделі;

. створення комп'ютерної моделі;

. перевірка правильності створеної комп'ютерної моделі.

Ця перевірка здійснюється для знаходження і виключення помилок, які були допущені в процесі розробки моделі. Іноді може з'ясуватися, що помилку було допущено не на даному етапі, а раніше. Наприклад, невдало вибраний метод, допущені надмірні спрощення при моделюванні і тому подібне. У такому разі потрібно повернутися до відповідного етапу, внести потрібні корективи і повторити наступні етапи побудови моделі.

Проведення комп'ютерного експерименту

Метою етапу є дослідження моделі і з'ясування на цій основі властивостей об'єкту моделювання.

Етап складається з таких дій:

. розробка плану дослідження;

. проведення комп'ютерного експерименту на базі створеної моделі;

. аналіз отриманих результат.

Результати проведеного експерименту характеризують властивості комп'ютерної моделі. Проте її адекватність об'єкту дослідження дає підставу для того, щоб вважати ці властивості властивими самому об'єкту.

В ході експерименту може виникнути потреба відкоректувати план дослідження, наприклад, поглибити його в деякому напрямі. Іноді отримані результати можуть виявитися сумнівними, що вимагатиме вибору іншого методу дослідження, або уточнення моделі, або навіть внесення змін, в постановку завдання, і тоді весь процес починається знову.

Для нашої задачі ми повинні спланувати і провести серію спроб для різних відстаней від стіни і різних початкових швидкостей каменя. Отримані результати дадуть нам підстави для виводу, чи має Робін Гуд шанс влучити каменем у вікно, і якщо так, то як йому це зробити.

2 Моделювання технічних систем на основі теорії подібнocтi

2.1 Поняття подібності

2.1.1 Геометрична noдібність

Проста геометрична подібність є найпростішим випадком подібності, яка полягає в наявності певних масштабних співвідношень вигляду

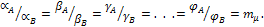(2.1)

для параметрів схожих елементів (довжин сторін, кутів і тому подібне) геометричних фігур А і В, які порівнюються. Іншими словами, багатокутники з однаковою кількістю сторін геометрично подібні, якщо в них однакові кути і пропорційні відповідні сторони.

Масштабні співвідношення (2.1) визначають правила переходу від параметрів одного з об'єктів до схожих napaметpiв іншого. Самі масштабні коефіцієнти m_l і т_μ , що визначають правила переходу і характеризують пропорційність схожих параметрів, називають коефіцієнтами noдібності.

Умова простої геометричної подібності (2.1) при введенні системи прямокутних координат XY може бути переформульована так: два багатокутники геометрично подібні тоді і тільки тоді, коли всі координати першого багатокутника x_iA, у_iA пропорційні відповідним координатам другого багатокутника x_iB, y_iB тобто виконується співвідношення:

(2.2)

де х_і , у_і - координати довільної точки, яка знаходиться на відрізках прямих, які визначають контури відповідних багатокутників A і В;

тх і ту – масштабні коефіцієнти подібності.

Якщо простір вимірюється більш ніж двома координатами, то геометричну подібність означає пропорційність всіх схожих координат об'єктів по всіх координатних осях. Наприклад, в тривимірному просторі XYZ повинна виконуватися умова:

2.1.2. Афінна подібність

Афінна подібність - це узагальнений варіант геометричної подібності, при якій допускається нерівність масштабних коефіцієнтів подібності по окремих координатах. При афінній подібності під час переходу від однієї фігури до іншої відбувається їх деформація: круги перетворюються на еліпси, паралелепіпеди з нерівними сторонами в куби і тому подібне. Для схожих координатних точок x_iA, у_iA, z_iA і x_iB, y_iB, z_iB тривимірного координатного простору в прямокутних декартових координатах у разі афінної подібності геометричних фігур A і В будуть справедливі співвідношення:

При цьому виникає потреба введення спеціальних функцій перетворення, переважно нелінійних, які встановлюють закономірності афінного перетворення на площині або в просторі.

2.1.3. Подібність технічних систем

Подібність моделі і оригіналу є невід'ємною умовою адекватності моделювання. Довільний фізичний процес або технічна система φ₀ характеризується функціональною залежністю φ₀ = F(P₁, P₂... P_j... Pn). Ця залежність може бути відображена в n- вимірному просторі, в якому параметрам процесу відповідатимуть координатні осі, причому, якщо одним из параметров Р_i, буде час, то одна з координатних вісей буде віссю часу. Аналогічно в тому ж координатному просторі може бути відображений процес Ф₀ = F(R₁, R₂... R_j... Rn), який характеризується параметрами R = { R _j }, похожими на Р = { Р_j }. Якщо при цьому всі схожі параметри (просторові координати) пропорційні, тобто виконується умова (1), то процеси φ₀ i Ф₀ будуть подібними:

(2.3)

2.2 Види подібності

По ступеню відповідності параметрів моделі і оригіналу розрізняють подібність абсолютну і практичну (неабсолютну).

Абсолютна подібність досягається тоді, коли у всі схожі моменти часу у всіх схожих точках простору всі параметри Р_j процесів і елементів в одній системі знаходяться в повній відповідності з схожими параметрами R_j віншій системі, тобто P_j / R_j = m_j, j =1,2...n, причому, можливо, т_j = const, m_j = var, m_j = f(P_j-k … P_j+k,…) і тому подібне. Отже, модель і оригінал будуть абсолютно подібними при повній відповідності геометричних розмірів систем, які зіставляються, і величин, які змінюються у просторі та часі, тобто процесів в цих системах.

При абсолютній подібності оригінал і модель структурно і фізично подібні; вони відрізняються лише значеннями параметрів, які характеризують елементи і зв'язки між ними. Процеси в моделі і оригіналі в цілому, так само як стани окремих елементів, описуються однаковими функціональними залежностями, які пропорційно відрізняються лише значеннями аргументів. Відтворення процесу на моделі здійснюється без яких або спотворень щодо оригіналу і відрізняється від нього лише масштабом.

У переважній більшості випадків вирішення конкретних завдань дослідник не має можливості працювати з явищами або системами, схожими абсолютно у всіх деталях. Тому виникає потреба введення

поняття практичної подібності, в межах якої розрізняють повну, неповну і наближену подібність.

Повна подібність - це подібність ходу в часі і просторі тих процесів, які є істотними для даного дослідження і з достатньою повнотою характеризують досліджуване явище з погляду конкретної постановки завдання дослідження. Наявність повної подібності визначають за відповідністю всіх схожих величин, які істотно впливають на хід цих процесів. Так, можна вважати повністю подібними електричні процеси в двох довільних послідовних RC-контурах, включених на джерело синусоїдальної напруги. При цьому теплові процеси можуть бути неподібними.

Неповна подібність - це подібність ходу процесів лише в просторі або лише в часі (наприклад, при подібності ходу перехідних процесів в двох електричних лініях розподіл електричного поля може бути разным в результаті різної геометрії проводів).

Наближена подібність характеризується існуванням спрощених допушень, які дозволяють вважати подібними процеси, що відрізняються, за рахунок свідомих спотворень деяких їх властивостей. Так, наближеним можна рахувати подібність двох генераторів, виявлену на основі їх спрощених рівнянь, які не враховують аперіодичну складову струму статора і періодичну складову струму ротора.

По адекватності фізичної природи подібних явищ подібність розділяють на математичне і фізичне (електричне, механічне, теплове і т. п.).

Математична подібність потребує відповідності схожих параметрів порівнюваних процесів різної фізичної природи. Математична подібність може бути повною, неповною і наближеною. Приклад математичної подібності - рівняння перехідного процесу RLC - контура, включеного на синусоїдальну напругу, і рівняння вимушених коливань маятника, підвішеного на пружині у в'язкому середовищі. Математично подібними будуть всі компонентні рівняння аналогічних компонентів у фізичних підсистемах різної природи.

Фізична подібність досягається при однаковій фізичній природі явищ. Воно теж може бути повним, неповним і наближеним.

При фізичній подібності механічним процесам в досліджуваній системі ставиться у відповідність механічні процеси в подібних нею системах, електричним - електричні і тому подібне. Деколи виділяють кінематичну (подібність швидкостей і прискорень), матеріальну (подібність мас окремих елементів системи) і динамічну (подібність сил тих, що викликають рух) подібність. Системи, подібні кінематично, матеріально і динамічно, вважаються механічно подібними. Електрична подібність існує при подібності електричних і магнітних полів, напруги, струмів і потужностей окремих елементів. Аналогічно, системи, в яких подібні теплові потоки і температура, мають теплову подібність і так далі.

Фізична подібність може встановлюватися не тільки для фізичних явищ, які підкоряються детермінованим законам, але і для стохастичних процесів; у цих випадках говорять про статистичну подібність.

2.3 Критерії подібності

Очевидно, що поняття подібності фізичних процесів або технічних систем є розвитком поняття афінної подібності. Проте для фізичних процесів не всі масштабні коефіцієнти тj можуть приймати незалежні значення в результаті взаимозависимостей параметрів процесу або системи між собою. Наприклад, при довільному виборі опору певного резистора і напруги на нім струм, який протікає через цей елемент, не може приймати довільного значення. Це створює можливість введення деяких узагальнених характеристик подібних процссов і систем, які є функціями груп залежних і незалежних змінних. Ці узагальнені характеристики отримали назву критеріїв подібності.

Критерій подібності — безрозмірна величина, складена з розмірних фізичних параметрів, що визначають дане фізичне явище. Рівність всіх однотипних критеріїв подібності для двох фізичних явищ і систем - необхідна і достатня умова фізичної подібності цих систем.

Приклади:

Критерій подібності в теоретичній механіці

Критерій подібності механічного руху виходить з рівняння, що виражає другий закон Ньютона і називається числом Ньютона:

,

де — сила, що діє на тіло; — його маса; — час;

— характерний лінійний розмір.

Критерії подібності в теорії пружності

При вивченні пружних деформацій конструкції під впливом зовнішніх сил основними критеріями подібності є коефіцієнт Пуассона для матеріалу конструкції:

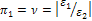і критерії , ,

де — відносна подовжинна деформація;

— відносна поперечна деформація;

— модуль Юнга; ρ — щільність матеріалу конструкції;

F — характерна зовнішня сила; g — прискорення сили тяжіння.

Критерії подібності в електричній системі

Хай електричний ланцюг складається з двох резисторів R₁ і R₂ і джерела ЕРС Е. Згідно другого закону Кірхгофа:

.

Представимо це рівняння у вигляді: .

Робимо рівняння безрозмірним: .

Звідси критерії подібності: ; .

Всяка нова комбінація з критеріїв подібності також є критерієм подібності, що дає можливість у кожному конкретному випадку вибрати найбільш зручні і характерні критерії.

Хай процес описується рівнянням F(x,y,q) = 0. Тоді критерії подібності:

Тут

де α_i, β_j, γ_к можуть набувати довільних значень, у тому числі і нульові.

У конкретному випадку, якщо, наприклад, процес описується інтегральним рівнянням F(x,y,q) = E – iR₁, - iR₂ = 0 маємо {q} = {R₁,R₂},

{x} = Е, {у} = i. Приведення до безрозмірного вигляду дає

1 – iR₁/E - iR₂/E = 0. Це означає, що для всіх подібних процесів повинна виконуватися умова

π₁ = iR₁ /E = = const,

π₂ = iR₂ /E = = const.

Звідси: С₁ = С₂ = 1; ; т.е. α₁ = α₂ = -1.

т.е. β₁ = β₂ = 1.

; т.е. γ₁ = 1.

; т.е. γ₁ = 0; γ₂ = 1.

Якщо відомі рівняння, що описують дане фізичне явище, то критерії подібності для цього явища можна отримати, приводячи рівняння до безрозмірного вигляду шляхом введення деяких характерних значень для кожного з визначальних фізичних параметрів, що входять в систему рівнянь. Тоді критерії подібності визначаться як безрозмірні коефіцієнти, що з'являються перед деякими з членів нової, безрозмірної системи рівнянь. Коли рівняння, що описують фізичне явище, невідомі, критерії подібності відшукуються за допомогою аналізу размерностей, що визначають фізичні параметри.

2.4 Теореми подібності

Забезпечення достовірності отриманих по модельних дослідженнях результатів при проведенні обмеженого числа експериментів при різноманітних поєднаннях параметрів вимагає необхідних і достатніх умов для існування подібності. Ці умови відбиті в трьох теоремах подібності, в яких сконцентрований результат численних досліджень. Перші дві теореми визначають необхідні, третя – необхідні і достатні умови подібності.

Перша теорема подібності, звана теоремою Ньютона або Ньютона—Бертрана, затверджує: що для подібних явищ повинні існувати однакові критерії подібності. У основному сучасному формулюванні, що враховує можливість існування різних видів подібності, перша теорема має наступний вигляд: явища, подібні в тому або іншому сенсі (повно, приблизно, фізично, математично і т. д.), мають певні поєднання параметрів, звані критеріями подібності, чисельно однакові для подібних явищ.

Перша теорема не указує способи встановлення подібності і способи його реалізації, вона лише формує необхідні умови існування подібності (однакові критерії подібності).

Друга теорема подібності, звана π – теоремою, затверджує: всяке повне рівняння фізичного процесу, записане в певній системі одиниць, може бути представлене функціональною залежністю між критеріями подібності, отриманими з параметрів цього процесу. Друга теорема встановлює можливість представлення інтеграла диференціального рівняння фізичного процесу не як функції параметрів процесу і системи, в якій протікають ці процеси, а як функція відповідним чином побудованих деяких безрозмірних величин — критеріїв подібності. Якщо початкове диференціальне рівняння проінтегрувало, то функціональні зв'язки між критеріями подібності будуть однозначно визначені відповідно до тих допущень, які були прийняті при складанні і інтеграції даного рівняння. Якщо ж диференціальне рівняння було відсутнє або не інтегрувалося, то вид функціональних зв'язків між критеріями подібності не буде виявлений. Пізніше, проте, Еренфест-афанасьева привела доказ того, що критерії подібності можна знайти і за відсутності диференціального рівняння процесу на основі аналізу размерностей фізичних величин, що беруть участь в цьому процесі. Ця можливість була сформульована і строго доведена у вигляді теореми, названою π-теоремой, оскільки згадані вище безрозмірні параметри (критерії подібності) позначалися буквою π.

Друга теорема так само, як і перша, не указує способів виявлення подібності і способів реалізації подібності.

Третя теорема подібності визначає необхідні і достатні умови подібності фізичних явищ. Третя теорема подібності утверж дає: необхідними і достатніми умовами для створення подібності явища, що вивчається, є:

· пропорційність подібних параметрів, що входять в умови однозначності;

· рівність критеріїв подібності явища, що вивчається.

Умови однозначності – це умови, що визначають індивідуальні особливості досліджуваного явища. Ці умови не залежать від механізму самого досліджуваного явища.

До них відносяться наступні чинники і умови:

· геометричні властивості системи, в якій протікає процес;

· фізичні параметри середовища і тіл, створюючих систему;

· початковий стан системи (початкові умови);

· умови на межах системи (граничне або краєві умови);

· взаємодія об'єкту і зовнішнього середовища.

Очевидно, не можна математично формулювати умови однозначності в загальному вигляді. У кожному конкретному випадку вони можуть бути різні залежно від роду вирішуваного завдання і виду рівняння. Так, наприклад диференціальне рівняння u = iR + Ldi/dt описує зміну струму в часі у ланцюзі з активним опором R і індуктивністю L при включенні її на u = const. Для виділення певного процесу з сукупності процесів, що описуються приведеним рівнянням, достатньо знати параметри u, R, L і початкові умови, наприклад,

i = i₀ при t = t₀.

Третя теорема подібності іменується також зворотною теоремою подібності або теоремою Кирпічева—Гухмана.

2.5 Аналіз розмірностей

Аналіз розмірностей виник як результат природного розповсюдження на фізичні явища понять геометричної подібності, відношення і пропорції. Дж. Фурье (1768–1830) вперше встановив, що існують певні основні одиниці вимірювання, щодо яких кожна фізична величина має визначені розмірності, які потрібно записувати як показники ступенів основних одиниць вимірювання.

Ідеї, лежачі в основі аналізу розмірностей, по суті очевидні і прості і базуються на фізичних законах (зв'язках між фізичними величинами), вони не залежать від свавілля у виборі основних одиниць вимірювання. З цієї ідеї на основі простих міркувань і застосування простого математичного апарату можна вивести важливе слідство: функції, які виражають фізичні закономірності, повинні володіти деякою фундаментальною властивістю, яка в математиці називається узагальненою однорідністю або симетрією. Ця властивість дозволяє записати шукані закономірності в безрозмірному вигляді, інваріантному щодо вибору систем одиниць вимірювання, з меншим числом аргументів (вже безрозмірних) і тим самим спростити їх (закономірностей) знаходження.

Одиниця вимірювання є мірою, за допомогою якої вимірюється та або інша фізична величина. Цим вимірюванням є пряме або непряме порівняння фізичних характеристик з відповідними (фізично подібними) еталонами, прийнятими за одиницю і званими одиницею вимірювання. Так, період напіврозпаду порівнюється з одиницею вимірювання – роком, швидкість літака порівнюється з одиницею вимірювання швидкості, рівній швидкості рівномірного руху, в якому шлях в один кілометр проходиться за час, рівний одній годині і так далі.

Величини, чисельні значення яких в даних питаннях залежать від вибору одиниць вимірювання, називаються розмірними величинами. Наприклад, енергію можна вимірювати в кілограмометрах, калоріях, тоннах вугілля, кілограмах урану, рублях і ще в багатьох інших одиницях вимірювання.

Одиниці вимірювання фізичних величин підрозділяються на основних і похідних. Величини, для яких одиниці вимірювання вводяться з досвіду за допомогою природних або штучних еталонів, по умові називаються первинними або основними. При цьому самі одиниці вимірювання також називаються первинними. Так, наприклад, для вивчення механічних рухів відомими способами вводяться первинні, або основні, одиниці вимірювання, такі, як довжина, час і маса, причому тут є певна свобода вибору. Так, для опису тих же механічних явищ можна прийняти еталони для сили, довжини і часу.

Одиниці вимірювання для інших величин, які виходять з визначення цих величин через первинних, називаються похідними або вторинними. Визначення фізичної величини завжди указує спосіб її вимірювання, принаймні уявний. Так, щільністю, згідно визначенню, є відношення маси до величини об'єму, який її укладає.

У різних областях науки і техніки вигідно і зручно вибирати як первинні одиниці вимірювання свої місцеві системи первинних одиниць вимірювання. Системою одиниць вимірювання називається сукупність основних одиниць вимірювання, достатня для вимірювання параметрів (характеристик) даного класу явищ. Виникли різні системи одиниць вимірювання і як наслідок – рутинне завдання про перехід (перерахунку) від однієї системи до іншої.

З 1960 року використовується Міжнародна система одиниць СІ (System International d’Unites), в якій основними одиницями вимірювання є метр, кілограм-маса і секунда.

Вираз похідної одиниці вимірювання через основні одиниці вимірювання називається її розмірністю. Розмірність виражає якісну суть фізичної величини, зміряної за допомогою даної системи одиниць вимірювання, і виходить автоматично з визначення цієї величини. Для позначення розмірності фізичних величин вводять символи. У системі СІ символи одиниць вимірювання для основних фізичних величин будуть: L для одиниці довжини, T для одиниці часу і M для одиниці маси. Розмірність деякої фізичної величини f прийнято за пропозицією Максвела позначати через [ f ]. Важливо підкреслити, що розмірність визначається класом систем одиниць вимірювання і в різних класах систем вимірювання розмірність одної і той же фізичної величини буде різною. Так, наприклад, розмірність сили F вкласі LMT буде [F] = MLT ^-2, а в класі MKS, де основними є метр, кілограм - сила и секунда, вона буде [F] = K. Таким чином, у формулі (у функції) розмірності для якої-небудь величини φ,

[φ] = L^α T ^β M ^γ. (2.4)

Аргументи L, T, M виступають як деякі позитивні числа, які можна перемножувати або ділити.

Величини, чисельне значення яких однаково у всіх системах одиниць вимірювання усередині даного класу, називаються безрозмірними, тобто для таких величин в (2.4) α = β = γ = 0. Очевидно, що розмірність безрозмірної величини рівна одиниці. Останні всі величини називаються розмірними.

Приведена вище формула (функція) розмірності фізичної величини (2.4) є степеневий одночлен. Природно виникає питання: чи є фізичні величини, для яких це не так, тобто їх розмірність наприклад в класі LTM, виражається у вигляді M sin L або lg T / e^M ? Насправді таких величин немає і розмірність будь-якої фізичної величини завжди є степеневим одночленом.

Говорять, що набір величин а₁ , а₂ ,…, а_к мають незалежні розмірності, якщо розмірність жодної з цих величин не можна представити у вигляді добутку ступенів розмірностей решти величин. Наприклад, розмірності щільності [ρ] = ML ^-3, прискорення [w] = LT ^-2 і сили [F] = MLT ^-2 незалежні; розмірності довжини [l] = L швидкості [v] = LT ^-1 і прискорення [w] = LT ^-2 залежні, оскільки між размерностями цих останніх величин має місце співвідношення [l] • [w] = [ v ² ].

Приклад 1.