Relative Error or Fractional Error

It is defined as the ratio of the error and the specified magnitude of the quantity. Mathematically we write as,

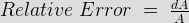
Where dA is the error and A is the magnitude.

Now here we are interested in computing resultant limiting error under the following cases: (a) By taking the sum of two quantities: Let us consider two measured quantities a₁ and a₂. The sum of these two quantities can be represented by A. Thus we can write A = a₁ + a₂. Now the relative incremental value of this function can be calculated as

Separating the each term as shown below and by multiplying and dividing a₁ with the first term and a₂ with the second term we have

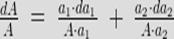
From the above equation we can see that the resultant limiting error is equal to the sum of products formed by multiplying the individual relative limiting errors by the ratio of each term to the function. Same procedure can be applied to calculate the resultant limiting error due to summation of more than two quantities. In order to calculate the resultant limiting error due to difference of the two quantities just change the addition sign with subtraction and rest procedure is same.

(b) By taking the product of two quantities: Let us consider two quantities a₁ and a₂. In this case the product of the two quantities are expressed as A = a₁.a₂. Now taking log both sides and differentiating with respect to A we have resultant limiting errors as

From this equation we can see that the resultant error is summation of relative errors in measurement of terms. Similarly we can calculate the resultant limiting error for power of factor. Hence the relative error would be n times in this case.

Types of Errors

Basically there are three types of errors on the basis; they may arise from the source.

Поиск по сайту: