ОИРМ ЕОСЮ ВТАЬ ЛГОП

Число магических квадратов быстро возрастает с увеличением размера квадрата. Существует только один магический квадрат размером 3х3. Количество магических квадратов 4х4 - 880, а 5х5 - 250000.

4.2.5 Метод перестановок на основе маршрутов Гамильтона

Этот метод реализуется путем выполнения следующих шагов.

Шаг 1. Исходный текст разбивается на блоки. Если длина шифруемого текста не кратна длине блока, то на свободные места последнего блока помещаются служебные символы-заполнители (например,*)

Шаг 2. Символами блока заполняется таблица, в которой для каждого порядкового номера символа в блоке отводится вполне определенное место (рисунок 4.10).

		Исходная таблица		Маршрут 1		Маршрут 2

Рисунок 4.10 - Вариант 8-элементной таблицы и маршрутов Гамильтона

Шаг 3. Считывание символов из таблицы осуществляется по одному из маршрутов. Увеличение числа маршрутов повышает криптостойкость шифра. Маршруты выбирают либо последовательно, либо их очерёдность задаётся ключом К.

Шаг 4. Зашифрованная последовательность символов разбивается на блоки фиксированной длины L. Величина L может отличаться от длины блоков, на которые разбивается исходный текст на шаге 1.

Расшифрование производится в обратном порядке.

Пример 5. Требуется зашифровать текст <МЕТОДЫ ПЕРЕСТАНОВКИ>. Ключ и длины зашифрованных блоков равны: К=<2,1,1>, L=4. Для шифрования использовать таблицу и два маршрута, представленные на рисунке 4.10.

Решение. Воспользуемся вышеизложенной методикой построения шифра по шагам.

Шаг 1. Исходный текст разбивается на 3 блока:

Блок =<МЕТОДЫ П>

Блок 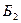=<ЕРЕС ТАНО>

=<ВКИ*****>

Шаг 2. Заполняется 3 матрицы с маршрутами 2,1,1 (рисунок 4.11).

		Маршрут 2

Рисунок 4.11 - Шифрование с помощью маршрутов Гамильтона

Шаг 3. Получение шифртекста путём расстановки символов в соответствии с маршрутами.

=< ОП_ТМЕЫДЕСРЕТАОНИ*КВ****>

Шаг 4. Разбиение на блоки шифртекста

=< ОП_Т МЕЫД ЕСРЕ ТАОН И*КВ ****>

Возможно применение и других маршрутов.

Поиск по сайту: