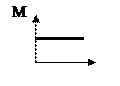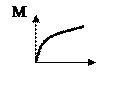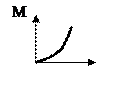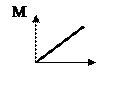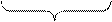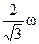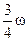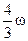| Задача № 1.4.1
|
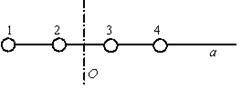
| Четыре шарика расположены вдоль прямой а. Расстояния между соседними шариками одинаковы. Массы шариков слева направо: 1 г, 2 г, 3 г, 4 г. Если поменять местами шарики 1 и 3, то момент инерции этой системы относительно оси 0, перпендикулярной прямой а и проходящей через середину системы …
| 
|
| 1.
| Не изменится
| 2.
| Уменьшится
| 3.
| Увеличится
|
|
|
|
|
|
|
|
| Задача № 1.4.2
|
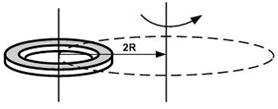
| При расчете моментов инерции тела относительно осей, не проходящих через центр масс, используют теорему Штейнера. Если ось вращения тонкостенной трубки перенести из центра масс на расстояние 2R (рис.), то момент инерции относительно новой оси увеличится в....
| 
|
| 1.
| 2 раза
| 2.
| 3 раза
| 3.
| 5 раз
| 4.
| 4 раза
|
|
|
|
|
|
| Задача № 1.4.3
|
| При расчете моментов инерции тела относительно осей, не проходящих через центр масс, используют теорему Штейнера. Если ось вращения тонкостенной трубки перенести из центра масс на образующую (рис.), то момент инерции относительно новой оси увеличится в …
| 
|
| 1.
| 4 раза
| 2.
| 2 раза
| 3.
| 3 раза
| 4.
| 1,5 раза
|
|
|
|
|
| Задача № 1.4.4
|
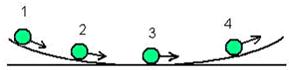
| Шарик скатывается по желобу, изогнутому в виде дуги окружности. Стрелкой указано направление линейной скорости центра масс шарика. Для положения 4 правильно указаны следующие направления углового ускорения и момента внешних сил...
| 
|
| 1.
| Угловое ускорение и момент сил совпадают с направлением скорости
|
| 2.
| Угловое ускорение направлено к нам. а момент сил направлен от нас перпендикулярно плоскости рисунка
|
| 3.
| Угловое ускорение и момент сил направлены к нам перпендикулярно плоскости рисунка
|
| 4.
| Угловое ускорение и момент сил направлены от нас перпендикулярно плоскости рисунка
|
| 5.
| Угловое ускорение и момент сил противоположны направлению скорости
|
|
|
| Задача № 1.4.5
|
| Диск вращается равномерно с некоторой угловой скоростью w. Начиная с момента времени t = 0, на него действует момент сил, график временной зависимости которого представлен на рисунке. Укажите график, правильно отражающий зависимость момента импульса диска от времени.
| 
|
| 1.
| 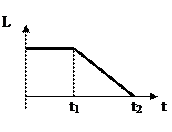
| 2.
| 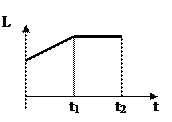
| 3.
| 
|
|
|
|
|
| Задача № 1.4.6
|
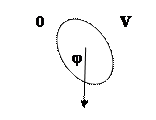
| Физический маятник совершает колебания вокруг оси, проходящей через т. 0 перпендикулярно плоскости рисунка. Для данного положения маятника момент силы тяжести направлен …
|     
|
| 1.
| От нас перпендикулярно плоскости рисунка
|
| 2.
| К нам перпендикулярно плоскости рисунка
|
| 3.
| Вниз в плоскости рисунка
|
| 4.
| Вверх в плоскости рисунка
|
|
|
|
|
| Задача № 1.4.7
|
Момент импульса тела относительно неподвижной оси изменяется по закону 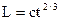 . Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело. . Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело.
|
|
| 1.
| 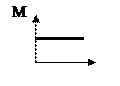
| 2.
| 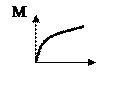
| 3.
| 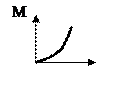
| 4.
| 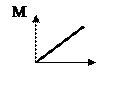
|
|
|
| Задача № 1.4.8
|
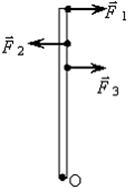
| К стержню приложены 3 одинаковые по модулю силы, как показано на рисунке. Ось вращения перпендикулярна плоскости рисунка и проходит через точку О. Вектор углового ускорения направлен...
| 
|
| 1.
| Влево
| 2.
| Вправо
|
| 3.
| Вдоль оси вращения 0 «к нам»
| 4.
| Вдоль оси вращения 0 «от нас»
|
|
|
|
|
| Задача № 1.4.9
|
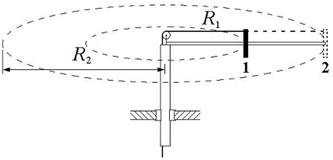
| Вокруг неподвижной оси с угловой скоростью ω1 свободно вращается система из невесомого стержня и массивной шайбы, которая удерживается нитью на расстоянии R1 от оси вращения. Отпустив нить, шайбу перевели в положение 2, и она стала двигаться по окружности радиусом R2 = 2R1 с угловой скоростью...
| 
|
| 1.
| ω2 = 1/2 ω1
| 2.
| ω2 = 4ω1
|
| 3.
| ω2 = 2ω1
| 4.
| ω2 = 1/4 ω1
|
| |
| Задача № 1.4.10
|
| Вокруг неподвижной оси с угловой скоростью ω1 свободно вращается система из невесомого стержня и массивной шайбы, которая удерживается нитью на расстоянии R1 от оси вращения. Потянув нить, шайбу перевели в положение 2, и она стала двигаться по окружности радиусом R2 = 1/2 R1 с угловой скоростью...
|        
|
| 1.
| ω2 = 4ω1
| 2.
| ω2 = 1/3 ω1
|
| 3.
| ω2 = 1/9 ω1
| 4.
| ω2 = 3ω1
|
| |
| Задача № 1.4.11
|
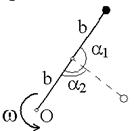
| Два невесомых стержня длины b соединены под углом α1 = 180° и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью ω. На конце одного из стержней прикреплен очень маленький массивный шарик. В некоторый момент угол между стержнями самопроизвольно уменьшился до α2=90°. Система стала вращаться с угловой скоростью...
| 
|
| 1.
| ω/2
| 2.
| 4ω
| 3.
| 2ω
| 4.
| ω/4
| 5.
| ω
|
|
|
|
|
|
|
|
|
|
| Задача № 1.4.12
|
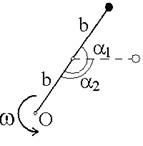
| Два невесомых стержня длины b соединены под углом α1=180° и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью ω. На конце одного из стержней прикреплен очень маленький массивный шарик. В некоторый момент угол между стержнями самопроизвольно уменьшился до α2 = 120о. Система стала вращаться с угловой скоростью …
| 
|
| 1.
| ω
| 2.
| 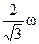
| 3.
| 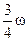
| 4.
| 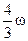
| 5.
| 
|
|
|
|
| Задача № 1.4.13
|
| Алюминиевый и стальной цилиндры имеют одинаковую высоту и равные массы. На цилиндры действуют одинаковые по величине силы, направленные по касательной к их боковой поверхности. Относительно моментов сил, действующих на цилиндры, справедливо следующее суждение …
|
|
| 1.
| Моменты сил, действующие на цилиндры; одинаковы
|
| 2.
| На алюминиевый цилиндр действует больший момент сил: чем на стальной цилиндр
|
| 3.
| На стальной цилиндр действует больший момент сил, чем на алюминиевый цилиндр
|
| 4.
| Моменты сил. действующие на цилиндры равны нулю
|
|
|
|
| Задача № 1.4.14
|
| Сплошной и полый цилиндры, имеющие одинаковые массы и радиусы, скатываются без проскальзывания с горки высотой h. К основанию горки...
|
|
| 1.
| Быстрее скатится сплошной цилиндр
|
| 2.
| Оба тела скатятся одновременно
|
| 3.
| Быстрее скатится полый цилиндр
|
|
|
| Задача № 1.4.15
|
| Два маленьких массивных шарика закреплены на невесомом длинном стержне на расстоянии r1 друг от друга. Стержень может вращаться без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей посередине между шариками. Стержень раскрутили из состояния покоя до угловой скорости ω.при этом была совершена работа А1. Шарики раздвинули симметрично на расстояние r2 = 3r1 и раскрутили до той же угловой скорости. При этом была совершена работа...
|

|
| 1.
| A2 = 1/9 А1
| 2.
| A2 = 3А1
|
| 3.
| A2 = 9А1
| 4.
| A2 = 1/3 А1
|
| |
| Задача № 1.4.16
|
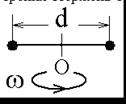
| Два маленьких массивных шарика закреплены на концах невесомого стержня длины d. Стержень может вращаться в горизонтальной плоскости вокруг вертикальной оси. проходящей через середину стержня. Стержень раскрутили до угловой скорости ω1. Под действием трения стержень остановился, при этом выделилось тепло Q1. Если стержень раскручен до угловой скорости ω2 =2ω1,то при остановке стержня выделится тепло...
|
|
| 1.
| Q2 = 4 Q1
| 2.
| Q2 = 1/4 Q1
|
| 3.
| Q2 = 1/2 Q1
| 4.
| Q2 = 2 Q1
|
|
|
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |






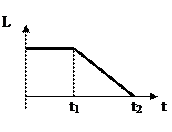
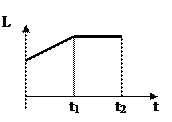






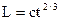 . Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело.
. Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело.