 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Теория автоматического управления
Учебно-методическое пособие
для выполнения курсовой и контрольной работ по специальности 1 53 01 07 “Информационные технологии и управление в технических системах“
для студентов заочной формы обучения
Минск БГУИР 2008
Содержание
Введение…………………………………………………………………………
1 Методическое указание по темам курса……………………………………..
2 Контрольная работа……………………………………………………………
3 Курсовая работа………………………………………………………………..
4 Компьютерное моделирование САУ ….…………………………….………
Литература………………………………………………………………………..
ВВЕДЕНИЕ
Автоматизация производственных процессов во всех отраслях народного хозяйства является одним из основных направлений научно-технического прогресса. Она призвана повысить производительность труда, улучшить качество продукции и облегчить условия труда.
В связи с этим значительно возрастает требование к освоению теории автоматического управления (ТАУ), являющейся специальной дисциплиной учебного плана специальности «Информационные технологии и управление в технических системах». В результате изучения курса специалист должен получить прочные знания о принципах построения систем автоматического управления (САУ), овладеть методами математического описания систем, освоить способы анализа и синтеза непрерывных и дискретных САУ. В процессе обучения студенты получают навыки исследования САУ на базе современной вычислительной техники и вырабатывают способность самостоятельно осваивать и применять в своей работе современные принципы и методы ТАУ.
Изучение дисциплины требует знания основных разделов высшей математики, физики, электротехники. Курс ТАУ базируется также на дисциплинах учебного плана «Математические основы теории систем», «Элементы и устройства систем управления» и ряде других.
Распределение курса по разделам и темам представлено в таблице 1.
Таблица 1
| Номер темы | Наименование темы | Кол-во часов на сам. раб. |
| Задачи теории автоматического управления. | ||
| 1.1 | Введение в проблематику управления техническими объектами. | |
| Линейные стационарные непрерывные САУ. | ||
| 2.1 | Математическое описание звеньев САУ. | |
| 2.2 | Математическое описание САУ. | |
| 2.3 | Точность САУ. | |
| 2.4 | Устойчивость САУ. | |
| 2.5 | Оценки качества переходных процессов. | |
| 2.6 | Обеспечение устойчивости, повышение качества регулирования и синтез линейных САУ. | |
| 2.7 | Векторно-матричные модели линейных САУ (уравнение состояния). | |
| Линейные стационарные импульсные САУ. | ||
| 3.1 | Математическое описание линейных импульсных систем. | |
| 3.2 | Точность импульсных САУ. | |
| 3.3 | Устойчивость импульсных САУ. | |
| 3.4 | Векторно-матричные модели линейных импульсных САУ (уравнения состояния). | |
| Нелинейные САУ. | ||
| 4.1 | Виды и особенности нелинейных САУ. | |
| 4.2 | Изображение переходных процессов на фазовой плоскости. | |
| 4.3 | Методы припасовывания и точечного преобразования. | |
| 4.4 | Автоколебания в системах высокого порядка. | |
| 4.5 | Исследование устойчивости нелинейных систем. | |
| 4.6 | Нелинейные импульсные системы. Цифровые САУ. | |
| Особые САУ. | ||
| 5.1 | Адаптивные САУ. | |
| 5.2 | Оптимальные САУ. | |
| 5.3 | Случайные процессы в САУ. |
Большое значение имеет самостоятельная работа с рекомендуемой литературой, выполнение контрольной и курсовой работы, а также цикла лабораторных работ.
Изучение всего курса разбито на два семестра.
В первом семестре изучаются разделы 1 и 2, выполняется контрольная работа, лабораторные работы и сдается экзамен.
В следующем семестре изучаются разделы 3, 4 и 5, выполняется курсовая работа, лабораторные работы и сдается экзамен.
Наиболее полно всему объему курса соответствует учебник [6], в конспективной форме материал курса изложен в [3, 4]. Разделы 1 и 2 можно изучать по учебникам [1, 2]. Следует также отметить, что содержание курса составляет классические разделы теории автоматического управления, поэтому при самостоятельном изучении курса можно рекомендовать любой учебник по теории автоматического управления.
1 МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ТЕМАМ КУРСА
Раздел 1. Задачи теории автоматического управления
Тема 1.1. Введение в проблематику управления техническими объектами
Предмет курса ТАУ и его задачи. Исторический очерк развития теории и техники управления. Основные понятия и термины ТАУ. Фундаментальные принципы управления. Примеры САУ. Классификация САУ. Основные законы регулирования.
[1, с. 3-10], [6, с. 9-35]
Раздел 2. Линейные стационарные непрерывные САУ
Тема 2.1. Математическое описание звеньев САУ
Дифференциальные уравнения звеньев в САУ. Линеаризация нелинейных уравнений. Весовая и переходная функции звеньев. Передаточная функция звена. Частотные характеристики звеньев. Классификация звеньев. Позиционные звенья САУ и их характеристики: идеальное усилительное, апериодическое, апериодическое второго порядка и колебательное. Интегрирующие звенья и их характеристики: идеальное интегрирующее и инерциальное интегрирующее звенья. Дифференцирующие звенья и их характеристики: идеальное дифференцирующее, идеальное звено с введением производной и инерциальное дифференцирующее звенья. Звенья неминимально фазового и минимально фазового типа. [1, с. 11-34], [6, с. 40-82]
Тема 2.2. Математическое описание САУ
Передаточные функции и характеристики разомкнутой цепи САУ. Последовательное и параллельное соединение звеньев, соединение с помощью обратной связи. Частотные характеристики разомкнутой цепи звеньев. Структурные преобразования. Передаточные функции замкнутой системы: главная передаточная функция, передаточные функции по ошибки и возмущению. Дифференциальное и характеристическое уравнение замкнутой системы. Частотные характеристики замкнутой системы.
[1, с. 27-34], [6, с.85-110].
Тема 2.3. Точность САУ
Процесс управления и требования к нему. Свободная, вынужденная и установившаяся составляющие процесса. Понятие точности и ошибки в САУ. Постоянные ошибки в статических и астатических системах. Точность при гармоническом воздействии. Установившаяся ошибка при произвольном воздействии. Коэффициенты ошибки.
[1, с. 60-66], [6, с. 190-198].
Тема 2.4. Устойчивость САУ
Понятие устойчивости линейных систем. Общая постановка задачи устойчивости по Ляпунову. Линеаризованные системы. Условия устойчивости линейных систем. Необходимые условия устойчивости. Алгебраические критерии устойчивости Рауса и Гурвица. Частотные критерии устойчивости Михайлова и Найквиста. Критерий Найквиста в логарифмической форме. Построение областей устойчивости. Метод Д-разбиения. Запасы устойчивости системы.
[1, с. 45-57], [6, с. 115-162].
Тема 2.5. Оценка качества переходных процессов
Требования качества и связь с частотными характеристиками. Показатели переходного процесса: время регулирования, перерегулирование. Частотные оценки качества. Оценки качества по вещественной частотной характеристике замкнутой САУ  . Оценки качества по логарифмическим характеристикам. Показатель колебательности. Построение переходного процесса по
. Оценки качества по логарифмическим характеристикам. Показатель колебательности. Построение переходного процесса по  . Корневые оценки качества: степень устойчивости, колебательность. Диаграммы Вышнеградского. Интегральные оценки качества.
. Корневые оценки качества: степень устойчивости, колебательность. Диаграммы Вышнеградского. Интегральные оценки качества.
[1, с. 68-76], [6, с. 200-223].
Тема 2.6. Обеспечение устойчивости, повышение качества регулирования и синтез линейных САУ
Корректирующие устройства последовательного и параллельного (параллельно-встречного) типа. Повышение точности в установившихся режимах. Инвариантность. Комбинированное управление по задающему и возмущающему воздействию. Влияние на точность общего коэффициента усиления разомкнутой системы и порядка астатизма. Обеспечение устойчивости и повышения запасов устойчивости. Частотный метод синтеза последовательных и параллельных корректирующих устройств. Формирование желаемой логарифмической частотной характеристики. Нахождение логарифмической характеристики корректирующего устройства. Определение передаточной функции корректирующего устройства.
[1, с. 105-122], [6, с. 258-286, 344-361].
Тема 2.7. Векторно-матричные модели линейных САУ (уравнение состояния)
Описание САУ в виде векторно-матричных уравнений (уравнений состояния). Характеристики многомерных систем: передаточная матрица, импульсная матрица, переходная матрица состояния. Вычисление реакции многомерных систем.Уравнения состояния в нормальной и канонической форме. Устойчивость многомерных систем. Управляемость и наблюдаемость.
[1, с. 82-100], [6, с. 103-110].
Раздел 3. Линейные стационарные импульсные САУ
Тема 3.1. Математическое описание линейных импульсных систем
Классификация импульсных систем. Описание импульсного элемента. Идеальный импульсный элемент. Формирующее устройство. Описание разомкнутой импульсной системы. Приведенная непрерывная часть системы. Уравнение разомкнутой импульсной системы во временной области. Аппарат дискретного преобразования Лапласа ( -преобразование,
-преобразование, 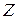 -преобразование). Передаточные функции разомкнутой импульсной системы. Свойства передаточных функций. Определение процессов в импульсных системах. Частотные характеристики импульсных систем и их свойства.
-преобразование). Передаточные функции разомкнутой импульсной системы. Свойства передаточных функций. Определение процессов в импульсных системах. Частотные характеристики импульсных систем и их свойства.
 - преобразование. Логарифмические частотные характеристики. Эквивалентность непрерывных и импульсных систем. Теорема Котельникова.
- преобразование. Логарифмические частотные характеристики. Эквивалентность непрерывных и импульсных систем. Теорема Котельникова.
[5, с. 3-40], [6, с. 406-422].
Тема 3.2. Точность импульсных САУ
Понятие точности и установившихся ошибок. Астатические импульсные САУ. Постоянные ошибки. Коэффициенты ошибок. Точность при гармоническом воздействии.
[6, с. 436-440].
Тема 3.3. Устойчивость импульсных САУ
Понятие устойчивости. Устойчивость линейных импульсных систем. Алгебраический критерий устойчивости Гурвица. Частотные критерии устойчивости Михайлова и Найквиста. Критерий Найквиста для логарифмических характеристик.
[6, с. 430-436].
Тема 3.4. Векторно-матричные модели линейных импульсных САУ (уравнение состояния)
Структурное представление дискретных САУ. Уравнения состояния. Нормальная и каноническая формы уравнений состояния. Передаточная и переходная матрицы состояния. Решение уравнений состояния.
[5, с. 46-68]
Раздел 4 Нелинейные САУ
Тема 4.1. Виды и особенности нелинейных САУ
Виды нелинейностей. Статические и динамические нелинейности. Фазовое пространство и фазовая плоскость. Особые точки и фазовые траектории. Типы особых точек и фазовые портреты линейных систем. Сепаратрисы, устойчивые и неустойчивые предельные циклы, автоколебания.
[6, с. 474-497].
Тема 4.2. Изображение переходных процессов на фазовой плоскости
Переходные процессы и автоколебания релейной системы. Системы со скользящим режимом. Системы с логическим управлением. Системы с переменной структурой.
[6, c. 501-513] [8, с. 9-20].
Тема 4.3. Методы припасовывания и точечного преобразования
Кусочно-линейные системы. Основы метода припасовывания. Определение переходного процесса в релейной системе методом припасовывания. Основы метода точечных преобразований. Примеры точечного преобразования в релейной системе.
[8, с. 20-34].
Тема 4.4. Автоколебания в системах высокого порядка
Исходные положения метода гармонической линеаризации (метода гармонического баланса). Применимость метода, свойство фильтра. Несимметричные и симметричные колебания. Коэффициенты гармонической линеаризации. Вычисление коэффициентов гармонической линеаризации. Алгебраический способ определения симметричных автоколебаний и устойчивости. Частотный способ определения симметричных автоколебаний. Несимметричные автоколебания. Постоянные ошибки.
[6, с. 533-596].
Тема 4.5. Исследование устойчивости нелинейных систем
Понятия устойчивости по Ляпунову для нелинейных систем. Устойчивость в малом, в большом, в целом, абсолютная устойчивость. Функции Ляпунова. Теоремы Ляпунова об устойчивости. Исследование нелинейных систем с помощью функции Ляпунова. Абсолютная устойчивость. Частотный критерий абсолютной устойчивости, теорема Попова.
[6, с. 513-530].
Тема 4.6. Нелинейные импульсные системы. Цифровые САУ
Способы нелинейной импульсной модуляции. Уравнения нелинейных импульсных систем с амплитудно-импульсной модуляцией. Уравнения импульсных систем с широтно-импульсной и время-импульсной модуляцией. Метод гармонической линеаризации. Устойчивость нелинейных импульсных систем. Теорема Ляпунова. Применение функций Ляпунова. Абсолютная устойчивость, критерий Попова. Цифровые системы автоматического управления и способы их описания.
[6, с. 445-473, с. 683-700].
Раздел 5. Особые САУ
Тема 5.1. Адаптивные САУ
Классификация адаптивных САУ. Самонастраивающиеся системы, поисковые и беспоисковые. Методы поиска экстремума: сканирование, метод Гауса-Зайделя, метод градиента, метод наискорейшего спуска. Принципы построения беспоисковых самонастраивающихся систем. Адаптивные системы с переменной структурой.
[6, с. 723-740].
Тема 5.2. Оптимальные САУ
Общая постановка задачи оптимального управления. Метод классического вариационного исчисления. Принцип максимума Понтрягина. Задача максимального быстродействия. Метод динамического программирования.
[6, с. 703-720].
Тема 5.3.Случайные процессы в САУ
Случайные процессы и их характеристики. Расчет линейных непрерывных САУ при случайных воздействиях. Случайные процессы в линейных импульсных системах. Статистическая линеаризация нелинейных элементов.
[6, с. 291-338]
2 Контрольная работа
Контрольная работа предусмотрена только для студентов заочной формы обучения. Для каждой контрольной работы приведено тридцать вариантов заданий. Студент должен выполнить вариант, номер которого совпадает с двумя последними цифрами номера его зачетки. В начале работы следует привести полностью задание и исходные данные, а в конце – список используемой литературы.
Оформляется контрольная работа в ученической тетради рукописным способом, либо печатается на компьютере на стандартных листах формата А4. Графики выполняются с соблюдением требований ЕСКД и следуют по ходу изложения текстового и расчетного материала. Работа предоставляется в деканат за три недели до начала экзаменационной сессии. Неряшливо оформленные работы могут быть возвращены студенту без рецензирования. В случае существенных замечаний работа отправляется на доработку. Если замечаний нет, а также при несущественных замечаниях, работа допускается к защите.
Расчеты в контрольной работе можно частично или полностью выполнять в ручную, либо выполнять с использованием ЭВМ. В разделе 5 “Компьютерное моделирование САУ” конспективно излагаются некоторые способы и методы моделирования систем автоматического управления с помощью пакета MatLab.
Исходные данные к контрольной работе
Структурная схема линейной САУ представлена на рис.1, где соответствующие передаточные функции имеют вид апериодических звеньев:
 ;
; 
 ;
; 
Параметры  ,
,  ,
,  ,
,  ,
,  для каждого варианта задания представлены в табл.1. Величина коэффициента
для каждого варианта задания представлены в табл.1. Величина коэффициента  выбирается далее из условия устойчивости.
выбирается далее из условия устойчивости.

Рис.1
Варианты задания приведены в таблице 2
Таблица 2
| Номер варианта |

|

|

|

|

|
| 0,01 | 0,2 | 0,06 | 16,5 | ||
| 0,02 | 0,3 | 0,07 | 1,1 | ||
| 0,03 | 0,4 | 0,08 | 15,5 | 1,2 | |
| 0,04 | 0,5 | 0,09 | 1,3 | ||
| 0,05 | 0,6 | 0,1 | 14,5 | 1,4 | |
| 0,06 | 0,7 | 0,15 | 1,5 | ||
| 0,07 | 0,8 | 0,2 | 13,5 | 1,6 | |
| 0,08 | 0,9 | 0,25 | 1,7 | ||
| 0,09 | 0,3 | 12,5 | 1,8 | ||
| 0,05 | 1,1 | 0,15 | 1,9 | ||
| 0,06 | 1,2 | 0,2 | 11,5 | ||
| 0,07 | 1,3 | 0,25 | 2,1 | ||
| 0,08 | 1,4 | 0,3 | 10,5 | 2,2 | |
| 0,09 | 1,5 | 0,35 | 2,3 | ||
| 0,1 | 1,6 | 0,4 | 9,5 | 2,4 | |
| 0,01 | 0,2 | 0,1 | 2,5 | ||
| 0,02 | 0,3 | 0,2 | 8,5 | 2,6 | |
| 0,03 | 0,4 | 0,3 | 2,7 | ||
| 0,04 | 0,5 | 0,4 | 7,5 | 2,8 | |
| 0,05 | 0,6 | 0,5 | 2,9 | ||
| 0,06 | 0,7 | 0,6 | 6,5 | ||
| 0,07 | 0,8 | 0,7 | 3,1 | ||
| 0,08 | 0,9 | 0,8 | 5,5 | 3,2 | |
| 0,09 | 0,9 | 3,3 | |||
| 0,1 | 1,1 | 0,4 | 4,5 | 3,4 | |
| 0,2 | 1,2 | 0,5 | 3,5 | ||
| 0,3 | 1,3 | 0,6 | 3,5 | 3,6 | |
| 0,4 | 1,4 | 0,7 | 3,7 | ||
| 0,5 | 1,5 | 0,8 | 2,5 | 3,8 | |
| 0,6 | 1,6 | 0,9 | 3,9 |
Задание
1. Найти передаточные функции разомкнутой и замкнутой системы:  при
при 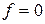 ,
,  (т.е. разомкнута главная обратная связь);
(т.е. разомкнута главная обратная связь);  при
при  - главная передаточная функция замкнутой системы;
- главная передаточная функция замкнутой системы;  при
при 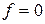 - передаточная функция замкнутой системы по ошибке;
- передаточная функция замкнутой системы по ошибке;  при
при  - передаточная функция замкнутой системы по возмущению. Параметры
- передаточная функция замкнутой системы по возмущению. Параметры  ,
,  входят в передаточные функции в общем виде, т.е. в буквенных символах.
входят в передаточные функции в общем виде, т.е. в буквенных символах.
2. Найти характеристическое уравнение замкнутой системы. Используя критерий Гурвица, записать в общем виде условия устойчивости. При заданных в табл.2 параметрах  ,
,  ,
,  ,
,  ,
,  найти максимальное граничное значение коэффициента передачи
найти максимальное граничное значение коэффициента передачи  при котором система еще устойчива. В дальнейшем полагать
при котором система еще устойчива. В дальнейшем полагать  .
.
3. Найти аналитические выражения и построить графики:
 − амплитудно-фазовой частотной характеристики (АФЧХ) разомкнутой системы;
− амплитудно-фазовой частотной характеристики (АФЧХ) разомкнутой системы;
 − амплитудно-частотной характеристики (АЧХ) разомкнутой системы;
− амплитудно-частотной характеристики (АЧХ) разомкнутой системы;
 − фазочастотной характеристики (ФЧХ) разомкнутой системы;
− фазочастотной характеристики (ФЧХ) разомкнутой системы;
 − логарифмических амплитудно- и фазо-частотных характеристик (ЛАЧХ и ЛФЧХ) разомкнутой системы;
− логарифмических амплитудно- и фазо-частотных характеристик (ЛАЧХ и ЛФЧХ) разомкнутой системы;
 - вещественной частотной характеристики замкнутой системы;
- вещественной частотной характеристики замкнутой системы;
 - амлитудно-частотный характеристики замкнутой системы.
- амлитудно-частотный характеристики замкнутой системы.
4. Используя полученные и построенные характеристики, найти и оценить следующие показатели качества системы:
-  -
-  статическую ошибку при подаче на ее входе единичного ступенчатого воздействия;
статическую ошибку при подаче на ее входе единичного ступенчатого воздействия;
- частоту среза системы  , запасы устойчивости системы по амплитуде
, запасы устойчивости системы по амплитуде  и фазе
и фазе  ;
;
- показатель колебательности системы  ;
;
- время регулирования  и перерегулирования
и перерегулирования  .
.
5.Найти дифференциальное уравнение замкнутой системы, связывающее 
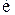
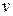 (полагаем
(полагаем  ).
).
6. Найти уравнения состояния замкнутой системы в векторно-матричном виде, в нормальной форме, связывающие координаты  и
и 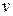 (полагаем
(полагаем  ).
).
Методические указания
1.Передаточные функции находятся с использованием правил структурных преобразований [1, с. 27-34].
2.Если найдена главная передаточная функция замкнутой системы в виде  , где
, где  − общий коэффициент передачи прямой цепи,
− общий коэффициент передачи прямой цепи,  полином относительно
полином относительно 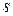 , то характеристическое уравнение замкнутой системы имеет вид:
, то характеристическое уравнение замкнутой системы имеет вид:
 .
.
Коэффициенты  зависят от параметров системы
зависят от параметров системы  ,
,  . Условие устойчивости в соответствии с критерием Гурвица для системы третьего порядка имеет вид
. Условие устойчивости в соответствии с критерием Гурвица для системы третьего порядка имеет вид  ,
,  . При заданных
. При заданных  из полученных условий устойчивости определяем ограничение на величину коэффициента передачи
из полученных условий устойчивости определяем ограничение на величину коэффициента передачи  и принимаем далее
и принимаем далее  . [1, c. 47-50].
. [1, c. 47-50].
3. Определение частотных характеристик и их построение подробно изложено в [1, c.17, 34]. АФЧХ  строится на комплексной плоскости. Ось абсцисс действительная
строится на комплексной плоскости. Ось абсцисс действительная  , а ось ординат мнимая
, а ось ординат мнимая  . Частота изменяется от
. Частота изменяется от  до
до 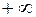 . Все остальные характеристики имеют ось абсцисс, на которой откладывается частота
. Все остальные характеристики имеют ось абсцисс, на которой откладывается частота  (для ЛАЧХ и АФЧХ в логарифмическом масштабе) и соответствующую ось ординат (это модуль или фаза).
(для ЛАЧХ и АФЧХ в логарифмическом масштабе) и соответствующую ось ординат (это модуль или фаза).
Все частотные характеристики строятся обычным способом. Задавая величину  дискретно
дискретно 
 ,
,  ,... Находят соответствующее значение ординаты и по точкам строят характеристику. ЛАЧХ
,... Находят соответствующее значение ординаты и по точкам строят характеристику. ЛАЧХ  обычно строится в виде асимптотической характеристики, состоящей из отрезков прямых.
обычно строится в виде асимптотической характеристики, состоящей из отрезков прямых.
4. Статическая ошибка определяется по формуле  , где
, где  . Частота среза
. Частота среза  определяется по графику ЛАЧХ. Это значение частоты, при котором
определяется по графику ЛАЧХ. Это значение частоты, при котором 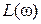 пересекает ось абсцисс и где
пересекает ось абсцисс и где  . Запасы устойчивости
. Запасы устойчивости  и
и  также находятся из логарифмических характеристик [1, с. 6]. Показатель колебательности определяют из графика амплитудно- частотной характеристики замкнутой системы
также находятся из логарифмических характеристик [1, с. 6]. Показатель колебательности определяют из графика амплитудно- частотной характеристики замкнутой системы  , как
, как 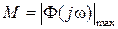 . Время регулирования
. Время регулирования  и перерегулирования
и перерегулирования  ориентировочно можно оценить, используя максимальное значение
ориентировочно можно оценить, используя максимальное значение  вещественной частотной характеристики
вещественной частотной характеристики  и частоту среза
и частоту среза  .
.
Графики, связывающие  ,
,  ,
,  и
и  представлены в [1, с. 15].
представлены в [1, с. 15].
5. Зная передаточную функцию, связывающую вход и выход системы, нетрудно получить дифференциальное уравнение, связывающее входную и выходную координаты системы [1, c. 15].
6. По дифференциальному уравнению, найденному в предыдущем пункте, легко найти уравнения состояния в нормальной форме [1, с. 90].
3. КУРСОВАЯ РАБОТА
Целью курсовой работы является проверка способности студента самостоятельно применять при решении задач на практике теоретические знания, полученные при изучении дисциплины.
Курсовая работа состоит из трех разделов (4.1, 4.2, 4.3), охватывающих теорию линейных непрерывных, импульсных и нелинейных САУ.
Документом, представляемым к защите курсовой работы, является расчетно-пояснительная записка, оформленная в соответствии с требованиями ЕСКД на стандартных листах писчей бумаги. Она содержит титульный лист, задания на курсовую работу и расчетную часть. Все графики выполняются на миллиметровки в выбранном масштабе и вклеиваются в записку по ходу изложения материала.
В расчетной части работы должны быть ссылки на используемую литературу, список которой приводится в конце записки. Номер варианта выбирается так же, как и для контрольных работ, т.е. по двум последним цифрам номера зачетной книжки. Работа может быть написана и оформлена рукописным способом или отпечатана на компьютере. Все расчеты могут проводиться вручную или с использованием ЭВМ. В последнем случае в разделе 5 настоящего методического пособия конспективно изложены методы расчета систем автоматического управления на ЭВМ с помощью пакета Matlab.
Курсовая работа представляется на проверку и рецензирование не менее чем за пятнадцать дней до начала сессии. После предварительного рецензирования работа либо возвращается на доработку, либо допускается к защите.
3.1. Исследование линейной непрерывной САУ
Исходные данные
Структура исследуемой замкнутой линейной непрерывной САУ представлена на рис. 2, где  – управляющее воздействие,
– управляющее воздействие,  – возмущающее воздействие,
– возмущающее воздействие, 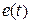 – сигнал ошибки,
– сигнал ошибки,  – выходной сигнал. Значения параметров
– выходной сигнал. Значения параметров 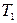 ,
,  ,
,  заданы в табл. 3. Размерность
заданы в табл. 3. Размерность  ,
,  ,
,  в секундах, общий коэффициент передачи
в секундах, общий коэффициент передачи  имеет размерность 1/с, в табл. 3 заданы также желаемые показатели качества системы: максимальная ошибка по скорости
имеет размерность 1/с, в табл. 3 заданы также желаемые показатели качества системы: максимальная ошибка по скорости  при скачке по скорости
при скачке по скорости  и
и  , время переходного процесса
, время переходного процесса  в секундах, и перерегулирование
в секундах, и перерегулирование  в процентах.
в процентах.

Рис.2
Таблица 3
| Номер варианта | 
| 
| 
|  , % , %
| 
| 
| 
|
| 2,5 | 0,1 | 3,0 | 0,55 | 1,9 | 1,8 | ||
| 2,0 | 0,08 | 3,1 | 0,3 | ||||
| 3,0 | 0,15 | 3,5 | 0,5 | 1,2 | 1,4 | ||
| 1,8 | 0,06 | 5,0 | 0,6 | 3,5 | |||
| 3,3 | 0,15 | 4,0 | 0,57 | 1,5 | |||
| 3,2 | 0,14 | 3,0 | 0,4 | ||||
| 1,6 | 0,08 | 2,5 | 0,5 | 1,9 | |||
| 1,8 | 0,07 | 1,5 | 0,58 | ||||
| 1,2 | 0,05 | 2,0 | 0,48 | ||||
| 1,4 | 0,04 | 2,5 | 0,33 | 1,9 | |||
| 1,9 | 0,06 | 3,0 | 0,63 | 1,2 | |||
| 2,3 | 0,08 | 3,5 | 0,34 | 2,3 | 4,5 | ||
| 2,7 | 0,1 | 4,0 | 0,49 | 1,1 | 1,5 | ||
| 2,6 | 0,08 | 3,5 | 0,34 | 1,6 | |||
| 2,8 | 0,06 | 3,8 | 0,23 | 4,8 | |||
| 1,5 | 0,02 | 2,5 | 0,45 | 0,5 | 1,8 | ||
| 3,5 | 0,1 | 2,0 | 1,2 | 1,8 | |||
| 3,2 | 0,08 | 1,5 | 1,4 | 2,4 | 2,1 | ||
| 2,8 | 0,1 | 3,0 | 0,15 | 2,8 | 3,6 | ||
| 2,5 | 0,1 | 4,2 | 0,48 | 2,3 | 1,7 | ||
| 1,4 | 0,06 | 2,5 | 0,27 | 2,4 | |||
| 1,6 | 0,06 | 2,5 | 0,33 | 3,5 | 4,3 | ||
| 1,8 | 0,05 | 4,0 | 0,1 | 1,8 | 1,1 | ||
| 2,6 | 0,08 | 3,0 | 0,56 | 2,5 | 4,9 | ||
| 2,8 | 0,08 | 2,8 | 0,5 | 1,6 | |||
| 2,4 | 0,07 | 1,5 | 0,47 | ||||
| 3,5 | 0,1 | 3,0 | 0,5 | 2,5 | 4,2 | ||
| 3,7 | 0,1 | 3,2 | 0,25 | 1,2 | 3,8 | ||
| 3,6 | 0,11 | 2,5 | 0,34 | 1,6 | 2,4 | ||
| 3,8 | 0,12 | 2,4 | 0,48 | 1,8 | 2,5 |
Задание
1. Найти передаточные функции: разомкнутой системы  ; замкнутой системы: главную передаточную функцию
; замкнутой системы: главную передаточную функцию  , по ошибке
, по ошибке  и по возмущению
и по возмущению  .
.
2. Построить область устойчивости системы в плоскости общего коэффициента передачи  и постоянной времени
и постоянной времени  при заданных значениях
при заданных значениях  и
и  . Найти граничное значение
. Найти граничное значение 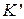 при заданном значении
при заданном значении  , при котором система выходит на границу устойчивости.
, при котором система выходит на границу устойчивости.
3. Построить графики логарифмических амплитудной и фазовой частотных характеристик (ЛАЧХ и ЛФЧХ) 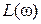 и
и  при значении коэффициента передачи
при значении коэффициента передачи  .
.
4. Оценить запасы устойчивости по модулю  и фазе
и фазе  , величину ошибки по скорости
, величину ошибки по скорости  при
при  ,
,  , время переходного процесса
, время переходного процесса  и перерегулирование
и перерегулирование  в исходной системе при
в исходной системе при  .
.
5. Если исходная система не удовлетворяет заданным в табл. 2 показателям качества  ,
,  ,
,  (хотя бы одному из них) или имеет малые запасы устойчивости, то провести коррекцию системы (последовательного или параллельного типа) и найти передаточную функцию корректирующего устройства.
(хотя бы одному из них) или имеет малые запасы устойчивости, то провести коррекцию системы (последовательного или параллельного типа) и найти передаточную функцию корректирующего устройства.
6. Вычислить в скорректированной системе переходный процесс на выходе  при подаче на вход единичной ступенчатой функции
при подаче на вход единичной ступенчатой функции  (
( ). Найти
). Найти  ,
,  по переходному процессу и сравнить их с заданными по заданию.
по переходному процессу и сравнить их с заданными по заданию.
Краткие методические указания
1. Передаточная функция разомкнутой системы  при
при  ; главная передаточная функция
; главная передаточная функция  при
при  ; передаточная функция по ошибке
; передаточная функция по ошибке  при
при  и по возмущению
и по возмущению  при
при  определяются на основе правил структурных преобразований [1, с. 27-34].
определяются на основе правил структурных преобразований [1, с. 27-34].
2. Передаточная функция разомкнутой исходной системы имеет вид  , где
, где  . Характеристическое уравнение замкнутой системы будет
. Характеристическое уравнение замкнутой системы будет
 ,
,
где при заданных из табл. 3 числовых значениях  и
и  коэффициенты
коэффициенты  будут зависеть от параметров
будут зависеть от параметров  и
и  . Применение критерия Гурвица [1] к характеристическому уравнению четвертого порядка дает следующие условия устойчивости:
. Применение критерия Гурвица [1] к характеристическому уравнению четвертого порядка дает следующие условия устойчивости:  .
.
Приравнивая в написанных соотношениях правые части нулю, получим в плоскости  и
и  границы устойчивости, ограничивающие некоторую область устойчивости. При заданном
границы устойчивости, ограничивающие некоторую область устойчивости. При заданном  находим граничное значение
находим граничное значение 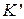 коэффициента передачи
коэффициента передачи  .
.
3. Полагая  находим выражение для
находим выражение для  ,
,  из
из  при
при  . Строим графики логарифмических характеристик [1, с. 34].
. Строим графики логарифмических характеристик [1, с. 34].
4. Запасы устойчивости по модулю и фазе определяются из логарифмических характеристик: на частоте среза  определяют
определяют  , а
, а  - на частоте при которой
- на частоте при которой  . Величина ошибки по скорости
. Величина ошибки по скорости 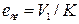 . Для ориентировочной оценки
. Для ориентировочной оценки  и
и  могут быть применены различные приближенные методы и формулы [1], либо следует построить переходной процесс
могут быть применены различные приближенные методы и формулы [1], либо следует построить переходной процесс  при
при 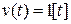 и из него определить
и из него определить  и
и  . В частности, можно воспользоваться следующим приемом. Найти вещественную частотную характеристику замкнутой системы
. В частности, можно воспользоваться следующим приемом. Найти вещественную частотную характеристику замкнутой системы  , построить ее график в низкочастотной области и найти максимальное значение ординаты
, построить ее график в низкочастотной области и найти максимальное значение ординаты  . Далее, зная
. Далее, зная  и частоту среза
и частоту среза  (находится из логарифмических характеристик) можно найти
(находится из логарифмических характеристик) можно найти  и
и  из диаграмм, связывающих
из диаграмм, связывающих  и
и  с величиной
с величиной  [1, с. 78].
[1, с. 78].
6. Если исходная система не удовлетворяет заданным показателям качества, ее следует скорректировать. Различие методики коррекции приводятся в [1, 6]. В случае частотных методов синтеза коррекции строится желаемая ЛАЧХ  . В низкочастотной части желаемой ЛАЧХ при сохранении порядка астатизма требуемый коэффициент усиления выбирается из соотношения
. В низкочастотной части желаемой ЛАЧХ при сохранении порядка астатизма требуемый коэффициент усиления выбирается из соотношения  . Частота среза при заданном
. Частота среза при заданном  и
и  выбирается по графику [1, с. 120]. На частоте среза желательно иметь наклон ЛАЧХ -20 дБ/дек с протяженностью этого участка не менее одной декады. Далее среднечастотная часть ЛАЧХ сопрягается с низкочастотной отрезком прямой с наклоном
выбирается по графику [1, с. 120]. На частоте среза желательно иметь наклон ЛАЧХ -20 дБ/дек с протяженностью этого участка не менее одной декады. Далее среднечастотная часть ЛАЧХ сопрягается с низкочастотной отрезком прямой с наклоном  дБ/дек, а высокочастотная часть желаемой и исходной ЛАЧХ по возможности должны совпадать.
дБ/дек, а высокочастотная часть желаемой и исходной ЛАЧХ по возможности должны совпадать.
Если найдена  , то в случае последовательной коррекции ЛАЧХ корректирующего устройства находится по выражению
, то в случае последовательной коррекции ЛАЧХ корректирующего устройства находится по выражению 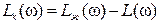 и далее по
и далее по 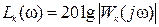 находим передаточную функцию корректирующего устройства
находим передаточную функцию корректирующего устройства  . Более подробно изложенная методика приведена в литературе [1, с. 118-122], [6, с. 355-360].
. Более подробно изложенная методика приведена в литературе [1, с. 118-122], [6, с. 355-360].
По логарифмическим частотным характеристикам следует для скорректированной системы найти запасы устойчивости по модулю и фазе. Считается, что приемлемыми на практике являются запасы устойчивости лежащие в следующих пределах: по модулю  , по фазе
, по фазе  .
.
6. Так как практически любые методики синтеза САУ, в том числе и методика, изложенная выше, являются приближенными, то завершающим этапом синтеза является проверочный расчет для скорректированной системы, который заключается в построении кривой переходного процесса, т.е. изменения выходной координаты  при подаче на вход единичного ступенчатого сигнала
при подаче на вход единичного ступенчатого сигнала 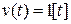 . По полученной переходной функции определяют для скорректированной системы величину
. По полученной переходной функции определяют для скорректированной системы величину  и
и  .
.
В настоящее время наиболее приемлемый метод вычисления кривой переходного процесса – это использование ЭВМ [1, с. 43]. При отсутствии такой возможности можно использовать графоаналитический метод, базирующийся на вещественной частотной характеристики замкнутой системы [2, с. 68].
3.2 Исследование линейных импульсных систем автоматического управления
Исходные данные
Анализируется одноконтурная замкнутая импульсная САУ, составляющая из непрерывной части (НЧ) и импульсного элемента (ИЭ), формирующего прямоугольные импульсы длительностью 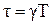 , где
, где 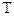 – период дискретизации,
– период дискретизации,  . Исходные данные для расчетов приведены в табл. 4. Для всех вариантов заданий передаточная функция непрерывной части имеет вид
. Исходные данные для расчетов приведены в табл. 4. Для всех вариантов заданий передаточная функция непрерывной части имеет вид
 .
.
Импульсный элемент представляется в виде идеального ключа и формирующего устройства с передаточной функцией
 .
.
Структурная схема системы представлена на рис. 3. В табл. 4  – постоянные времени имеют размерность секунды,
– постоянные времени имеют размерность секунды,  – коэффициент передачи НЧ имеет размерность
– коэффициент передачи НЧ имеет размерность  и выбирается далее.
и выбирается далее.

Рис. 3
Таблица 4
| Номер варианта | 
| 
| 
| 
|
| 0,3 | 0,1 | |||
| 0,3 | 0,9 | 0,9 | 0,2 | |
| 0,3 | 0,8 | 0,8 | 0,2 | |
| 0,3 | 0,7 | 0,7 | 0,1 | |
| 0,3 | 0,6 | 0,6 | 0,1 | |
| 0,3 | 0,5 | 0,5 | 0,2 | |
| 0,3 | 0,4 | 0,4 | 0,2 | |
| 0,3 | 0,3 | 0,3 | 0,1 | |
| 0,3 | 0,2 | 0,2 | 0,1 | |
| 0,3 | 0,1 | 0,1 | 0,05 | |
| 0,5 | ||||
| 0,5 | 0,9 | 0,9 | ||
| 0,5 | 0,8 | 0,8 | ||
| 0,7 | 0,7 | 0,7 | ||
| 0,7 | 0,6 | 0,6 | ||
| 0,7 | 0,5 | 0,5 | ||
| 0,7 | 0,4 | 0,4 | ||
| 0,8 | 0,3 | 0,3 | ||
| 0,8 | 0,2 | 0,2 | ||
| 0,8 | 0,1 | 0,1 | ||
| 0,9 | 0,9 | |||
| 0,8 | 0,8 | |||
| 0,7 | 0,7 | |||
| 0,6 | 0,6 | |||
| 0,5 | 0,5 | 0,1 | ||
| 0,4 | 0,4 | 0,1 | ||
| 0,3 | 0,3 | 0,1 | ||
| 0,2 | 0,2 | 0,01 | ||
| 0,1 | 0,1 | 0,01 |
Задание
1. Найти передаточные функции импульсной САУ:  – разомкнутой системы,
– разомкнутой системы, 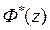 – замкнутой системы,
– замкнутой системы,  – передаточную функцию системы по ошибке. Параметры
– передаточную функцию системы по ошибке. Параметры  входят в выражения передаточных функций в общем виде, т.е. в буквенном виде. Далее в пункте 4.2 знак
входят в выражения передаточных функций в общем виде, т.е. в буквенном виде. Далее в пункте 4.2 знак  будет относиться к передаточным функциям импульсной системы.
будет относиться к передаточным функциям импульсной системы.
2. Найти интервал изменения коэффициента передачи  , при котором система будет устойчива
, при котором система будет устойчива  . Для дальнейших исследований выбрать значение
. Для дальнейших исследований выбрать значение 
3. Построить графики логарифмических частотных характеристик разомкнутой импульсной системы 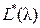 и
и  при заданных значениях
при заданных значениях  и выбранном
и выбранном  . По графикам определить запасы устойчивости системы по модулю
. По графикам определить запасы устойчивости системы по модулю  и фазе
и фазе  .
.
4. Определить ошибку по скорости  системы при входном воздействии
системы при входном воздействии  (скачок по скорости), а также первые два коэффициента ошибок
(скачок по скорости), а также первые два коэффициента ошибок  .
.
5. Вычислить переходной процесс в системе при воздействии  (скачок по положению).
(скачок по положению).
Краткие методические указания
Поиск по сайту: