Иван Матвеевич Виноградов

Родился в селе Милолюб Великолукского уезда бывшей Псковской губернии в семье сельского священника. Получив среднее образование в реальном училище, Виноградов в 1910 г. поступил на мате­матическое отделение физико-математического факультета Пе­тербургского университета, курс которого он закончил в 1914 г. Ввиду больших успехов в математических науках его оставили при университете для продолжения научной деятель­ности ив 1918 г. назначили доцентом в Пермский университет, где вскоре он стал профессором. С 1920 г. Виноградов пере­шел работать в Петроград и там вел лекции в различных выс­ших учебных заведениях. В 1929 г. он получил звание академи­ка и с 1932 г. выполнял ответственную научную работу, состоя директором Математического института им. Стеклова при Ака­демии наук СССР.

Научная деятельность И. М. Виноградова сосредоточена главным образом на аналитической теории чисел, в которую он ввел совершенно новые методы исследований, позволившие этой отрасли математики получить в дальнейшем очень широ­кое развитие. Его книга «Новый метод в аналитической тео­рии чисел» удостоена Государственной премии первой степени. В методе, развиваемом Виноградовым в этой книге, исполь­зуются весьма деликатные математические понятия, и он труд­нодоступен для лиц, не обладающих специальными знаниями, но результаты применения этого метода представляют интерес даже для школьников.

Виноградов применил свой метод к решению двух истори­ческих проблем, одна из которых носит название «проблемы Варинга», а другая — «проблемы Гольдбаха», над решением которых безуспешно трудились уже около двух столетий са­мые крупные математики. Метод Виноградова дал блестящие результаты.

Первая проблема сформулирована в 1770 г. английским математиком Варингом (1734—1798) и выражается так: «до­казать, что всякое целое число N может быть представлено в виде суммы не более чем четырех квадратов». Например:

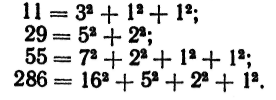
В последующие годы было доказано, что всякое натураль­ное число может быть представлено не более чем восемью ку­бами, семнадцатью четвертыми степенями и пр., но в общем виде эту теорему доказал только Виноградов, и при этом ему удалось дать весьма точную оценку числа необходимых сла­гаемых. Граница для числа слагаемых была выражена величи­ной равной

где п — показатель степени слагаемых.

Вторая проблема связана с именем одного из первых ака­демиков Петербургской Академии наук — уроженца города Кенигсберга Христиана Гольдбаха (1690—1764).

Эта проблема имела следующее происхождение. В письме к Л. Эйлеру, написанном в 1742 г., Гольдбах высказал пред­положение, что каждое натуральное число, большее шести, является суммой трех простых чисел. В своем ответе на это письмо Л. Эйлер сообщил, что, по его мнению, каждое четное число представляет сумму двух простых чисел, но что доказа­тельства этого положения он не имеет. Из этого вытекает след­ствие, что всякое нечетное число может быть представлено как сумма трех простых чисел. Ввиду того что все попытки доказать это на первый взгляд простое положение не давали никаких положительных результатов, считалось, что оно недо­казуемое при существующих в настоящее время математиче­ских средствах. Это и высказал на международном математи­ческом конгрессе в Кембридже в 1812 г. немецкий математик профессор Геттингенского университета, специалист в области аналитической теории чисел — Эдмунд Ландау (1877—1938). Он заявил: «Проблема Гольдбаха превосходит силы современ­ной математики». И он был прав: для доказательства пробле­мы Гольдбаха нужны были новые методы, которые и были предложены Виноградовым.

Проблема Гольдбаха была разрешена в 1937 г., когда Ви­ноградов сумел показать, что для достаточно больших нечетных чисел теорема справедлива. При этом «достаточно боль­шое число», согласно более поздним исследованиям математи­ка Бороздкина, оказалось равным приблизительно числу, ко­торое выражается так:

где е= 2,71828... Если бы это число можно было записать в развернутом виде, то его запись обернулась бы вокруг земно­го экватора 100 миллионов раз.

Методы, введенные Виноградовым, прочно вошли в науку и используются многими советскими и зарубежными учеными в их теоретических исследованиях. За свои заслуги перед нау­кой И. М. Виноградов награжден двумя орденами Ленина и медалями.

Николай Григорьевич Чеботарев (1894—1947)

Обучаясь еще в младших классах Каменец-Подольской гимназии, Н.Г.Чеботарев про­явил большой интерес к математике. Поступив на математи­ческое отделение физико-математического факультета Киев­ского университета, он стал одним из наиболее талантливых учеников выдающегося алгебраиста Д. А. Граве. Чеботарев заканчивал курс университета уже в Саратове, куда был эва­куирован Киевский университет во время первой мировой вой­ны. По окончании учебы Чеботарев был оставлен при универ­ситете. В 1921 г. он начал свою научно-педагогическую работу в Одессе, где и создал много глубоких по содержанию научных работ в области алгебры. В особенности высокую оценку в научном мире получила его работа по вопросу о бесконечности множества простых чисел, принадлежащих к заданному клас­су подстановок группы Галуа. В дальнейшем эта работа по­служила основой докторской диссертации Чеботарева, защи­щенной им в 1926 г. при Киевской Академии наук. В 1927 г. он был приглашен профессором в Казанский государственный университет, где и работал до конца жизни.

Казанский период жизни Чеботарева был временем наибо­лее высокого подъема его творческих сил. Им были проведены глубокие исследования по теории Галуа и создана так назы­ваемая теория резольвент для решения уравнений высших сте­пеней.

Резольвентой уравнения

Проблема, поставленная и разрешенная Н. Г. Чеботаре­вым, заключалась в том, чтобы коэффициенты уравнения (2) зависели от наименьшего числа параметров. Он первый указал подход к решению вопроса и разработал методы для даль­нейшего развития теории резольвент.

Методы современной алгебры своим развитием во многом обязаны трудам Чеботарева по вопросам теории групп Ли, диофантовых приближений и теории целых аналитических функций. Следует также отметить его труды по исследованию расположения корней уравнения.

Работая в области научных изысканий с большим энтузи­азмом, Чеботарев заражал им своих учеников, которые с боль­шим успехом продолжали разработку его идей. Это способст­вовало тому, что около Чеботарева сплотился широкий круг молодых ученых, заинтересованных решением алгебраических проблем, и таким образом зародилась возглавляемая им алге­браическая школа, центром которой являлась кафедра алгеб­ры Казанского университета, руководимая Чеботаревым.

Научную работу Чеботарев всегда сочетал с работой в об­ласти методики преподавания математических дисциплин. Хотя он и не имел печатных трудов, отражающих его взгляды на методику изложения математических дисциплин, но много работал по созданию учебников элементарной математики. Так, с 1939 по 1941 г. он возглавлял группу преподавателей по созданию учебника арифметики для школ взрослых. С особым интересом он работал с середины тридцатых годов до послед­них дней своей жизни над созданием руководства по элемен­тарной геометрии. К сожалению, он не успел его завер­шить. Уже после смерти Чеботарева этот не вполне закончен­ный труд был рассмотрен крупными специалистами и получил высокую оценку как прекрасный материал для создания школьного учебника.

Безвременная смерть Чеботарева прервала его исследова­ния, имеющие большие научные и практические приложения.

Большие заслуги Чеботарева для развития математики и математического просвещения были высоко оценены партией и правительством Советского Союза еще при его жизни: он был награжден орденом Ленина и двумя другими орденами и медалью; кроме того, в 1929 г. он был избран членом-кор­респондентом АН СССР, а в 1943 г. ему было присвоено зва­ние заслуженного деятеля науки РСФСР. За работы по проб­леме резольвент Н. Г. Чеботарев был удостоен в 1947 г. (по­смертно) Государственной премии первой степени.

Павел Сергеевич Александров — советский ма­тематик

С 1929 г. член-корреспондент Академии наук СССР, а с 1953 г. — академик, Герой Социалистического Труда (1969 г.), лауреат Государственной премии — родился в г. Богородске (ныне г. Ногинск Московской области). Закончил курс гимназии с золотой медалью. Окончив курс Московского университета в 1917 г., с 1921 г. П. С. Александров работал в нем сначала доцентом, а затем профессором. С 1932 г. он президент Московского математического общества. Является основателем Московской топологической школы. В начале сво­ей научной деятельности получил много значительных резуль­татов в области теории множеств, теории функций действи­тельного переменного. Занявшись вопросами топологии, соз­дал один из основных ее разделов — теорию бикомпактных пространств. Ныне П. С. Александров — глава советской топо­логической школы и широко известен не только в Советском Союзе, но и за рубежом. Он состоит иностранным членом-кор­респондентом Берлинской академии наук, иностранным чле­ном Американского философского общества в Филадельфии, членом Национальной академии наук в Вашингтоне (с 1947 г.), членом Геттингенской академии наук и других иностранных обществ.

Мстислав Всеволодович Келдыш (1911 —1978)

Видный советский ученый в области механики и математики — родил­ся в г. Риге. В 1931 г. он окончил курс Московского универси­тета, с 1943 г.— член-корреспондент АН СССР, а с 1946 г.— академик. За теорию, расчет и разработку мер устранения вибраций на самолете и за исследования теории и методов расчета автоколебаний самолетных конструкций был дважды награжден Государственными премиями (в 1942 и в 1946 гг.). Основные его научные работы относятся к вопросам теории колебаний, аэродинамики, теории волн на поверхности тяже­лой жидкости, удара о воду, приближенного интегрирования дифференциальных уравнений, теории потенциала, конформ­ных отображений и теории приближения функций комплексно­го переменного рядами полиномов. За огромные заслуги М. В. Келдыш был выдвинут на высокий пост президента Ака­демии наук СССР (1961 г.) и занимал его до конца жизни.

Поиск по сайту: