Составим симплекс-таблицу

В столбец X_Б вписываем переменные составляющие базис. В столбец с^Б коэффициенты при базисных переменных в целевой функции. Остальные столбцы заполняем данными из системы ограничений (коэффициентами при соответствующих переменных). В строку d вписываем оценки вычисленные по формулам: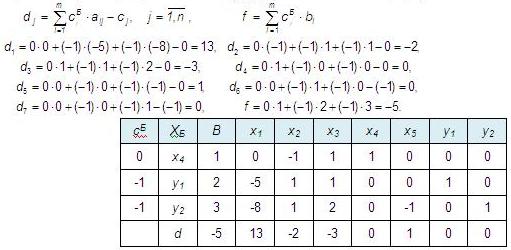

Среди оценок есть отрицательные, значит решение не оптимально. Минимальная среди оценок -3, переменная x₃ в базис войдет. Далее вычисляем оценочные отношения для этого столбца (делим построчно элементы столбца В на положительные элементы столбца x₃) и выбираем минимальное равное 1. Следовательно, переменная x₄ из базиса выйдет. Выделенный элемент будет разрешающим:

Преобразуем симплекс-таблицу, отбросив столбец с^Б:

Среди оценок опять есть отрицательные, поэтому продолжим преобразования:

Все оценки неотрицательные, искусственные переменные вышли из базиса, а значение функции равно 0. Теперь можно отбросить столбцы, содержащие искусственные переменные, и пересчитать оценки в соответствии с целевой функцией

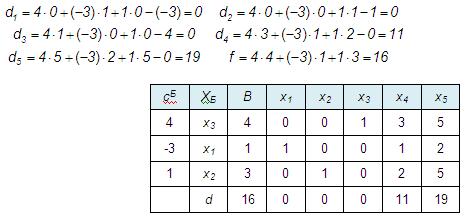
Все оценки снова получились неотрицательные, следовательно, решение оптимально:

x₁ =1, x₂ =3, x₃ =4, а максимум функции равен 16.

Поскольку исходная задача была на минимум, то надо умножить значение целевой функции на (-1). Получим Z_min = – 16.

Ответ: x ₁= 1, x ₂=3, x ₃=4, Z _min= –16

РЕШЕНИЕ ЗАДАЧ ЦЕЛОЧИСЛЕННОГО ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ МЕТОДОМ ГОМОРИ

Сущность метода Гомори решения задачи целочисленного линейного программирования состоит в том, что сначала задача решается без условия целочисленности. Если полученное решение целочисленное, то задача решена. В противном случае к ограничениям задачи добавляется новое ограничение, обладающее следующими свойствами:

· оно должно быть линейным;

· должно отсекать найденное оптимальное нецелочисленное решение;

· не должно отсекать ни одного целочисленного решения.

Далее задача решается с учетом этого нового ограничения. После этого в случае необходимости добавляется еще одно ограничение и т.д.

Рассмотрим задачу целочисленного линейного программирования вида:

Будем решать ее без условия целочисленности симплекс-методом. Если в результате полученное оптимальное решение окажется целочисленным, вычисления заканчиваем.

В противном случае строим дополнительное ограничение. Для этого среди элементов столбца В финальной симплекс-таблицы ищем нецелочисленные, если таких несколько, то берем максимальное b_s и составляем дополнительное ограничение по строке s:

Далее введением дополнительной неотрицательной целочисленной переменной преобразуем это неравенство в уравнение:

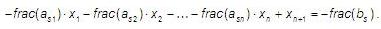
Включаем его в симплекс-таблицу и решаем двойственным симплекс-методом.

Алгоритм двойственного симплекс-метода

Получив оптимальное решение, проверяем его на целочисленность и если оно окажется не целочисленным, повторяем процедуру с дополнительным ограничением.

Пример. Решить методом Гомори задачу целочисленного линейного программирования:

x₁,x₂ – целые числа

Решение:

Сначала решим симплекс-методом задачу без учета условия целочисленности. Для этого приведем ее к стандартному виду:

Составим симплекс-таблицу, в столбец X_Б вписываем переменные составляющие базис. Остальные столбцы заполняем данными из системы ограничений (коэффициентами при соответствующих переменных):

В строку d вписываем оценки вычисленные по формулам:

Среди оценок есть отрицательные, значит решение не оптимально. Минимальная среди оценок -3, переменная x₁ в базис войдет. Далее вычисляем оценочные отношения для этого столбца (делим построчно элементы столбца В на положительные элементы столбца x₁) и выбираем минимальное равное 6. Следовательно, переменная x₄ из базиса выйдет. Выделенный элемент будет разрешающим:

Все оценки получились неотрицательные, следовательно, из этой таблицы получаем x₁ =19/2, x₂ =7/2,т.е. решение не целочисленное, поэтому строим дополнительное ограничение по второй строке (ей соответствует максимальное нецелое значение из столбца b):

Получим целочисленное решение x ₁= 9, x ₂=4

Ответ: x ₁= 9, x ₂=4, Z _max= 35

Начало формы

Поиск по сайту: