АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

РЕШЕНИЕ МАТРИЧНЫХ ИГР

Читайте также:
  1. I. Решение логических задач средствами алгебры логики
  2. II. Решение логических задач табличным способом
  3. III. Разрешение споров в международных организациях.
  4. III. Решение логических задач с помощью рассуждений
  5. MFG/PRO – лучшее решение для крупных и средних промышленных предприятий с дискретным типом производства
  6. Анализ матричных данных (матрица приоритетов)
  7. Антиполия-противоречие в в законе. Противоречие разрешаясь делает чего то возможным. Отрицание-отрицания ( разрешение противоречия (синтез))
  8. Арбитражное разрешение международных споров в Древней Греции
  9. Арбитражное разрешение международных споров в Древнем Риме
  10. Б) Правовое разрешение конфликтов
  11. В результате получаем общее решение системы
  12. Волновое уравнение и его решение. Физический смысл волнового уравнения. Скорость распространения волн в различных средах.

Рассмотрим парную конечную игру с заданной положительной платежной матрицей:

Можно решить симплекс-методом любую из взаимно-двойственных задач, а решение второй найти с помощью теорем двойственности.

Пример. Найти оптимальные смешанные стратегии игроков матричной игры с заданной платежной матрицей:

Решение:

Платежная матрица задает игру двух игроков А и В, каждый из которых имеет по три стратегии. Составим таблицу и определим нижнюю и верхнюю цены игры:

Составим симплекс-таблицу и решим ее.

Установим соответствие между переменными двойственных задач и найдем неизвестные xi:

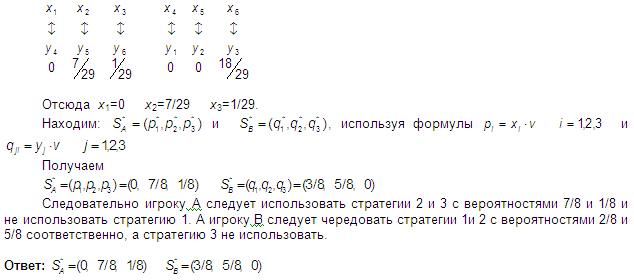
РЕШЕНИЕ ЗАДАЧ ДЛЯ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ

Будем рассматривать многоканальную систему массового обслуживания с неограниченной очередью.

Пусть имеется n -канальная СМО с неограниченной очередью. Поток заявок, поступающих в СМО, имеет интенсивность λ, а поток обслуживания имеет интенсивность μ. Найдем предельные вероятности состояний и показатели ее эффективности.

Начало формы

 

Конец формы

 

Конец формы

 


1 | 2 | 3 | 4 | 5 | 6 | 7 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)