 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
курс , 2 семестр
Примерный тест по дисциплине «Высшая математика»
Для самостоятельной работы студентов заочной формы обучения
Специальностей: БУ, ФМ, ЭУП, ФИК
курс, 2 семестр
1. Определенный интеграл 
равен:
a) [ ] 1.
b) [ ] 8;
c) [ ] 32;
d) [ ] 0.
2. Какая из приведенных функций является бесконечно большой функцией при 
:
a) [ ] 
;
b) [ ] 
;
c) [ ] 
;
d) [ ] 
.
3. Какой из интегралов вычисляется с помощью универсальной тригонометрической подстановки:
a) [ ]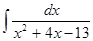 
;
b) [ ] 
.
c) [ ] 
;
d) [ ] 
.
4. Площадь фигуры, ограниченной сверху и снизу графиками функций 
и 
, слева и справа – прямыми 
и 
вычисляется по формуле:
a) [ ] 
;
b) [ ] 
.
c) [ ] 
;
d) [ ] 
;
5. Радиус сходимости степенного ряда вычисляется по формуле:
a) [ ] 
.
b) [ ] 
;
c) [ ] 
;
d) [ ] 
.
6. Какая из приведенных функций не является элементарной:
a) [ ] 
;
b) [ ] 
.
c) [ ]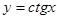 
;
d) [ ] 
.
7. Производная функции 
равна:
a) [ ] 
;
b) [ ] 
;
c) [ ] 
;
d) [ ] 
.
8. Если при переходе через критическую точку 
производная 
меняет знак с “–” на “+“, то есть:
a) [ ] точка минимума;
b) [ ] точка максимума;
c) [ ] точка разрыва.
d) [ ] точка перегиба.
9. Дифференциал произведения двух дифференцируемых функций 
и 
определяется по формуле:
a) [ ] 
;
b) [ ] 
;
c) [ ] 
;
d) [ ] 
;
10. Сумма двух непрерывных в точке функций есть:
a) [ ] функция, имеющая в точке устранимый разрыв.
b) [ ] функция, непрерывная в точке ;
c) [ ] функция, имеющая в точке разрыв первого рода;
d) [ ] функция, имеющая в точке разрыв второго рода.
11. Предел 
равен:
a) [ ] 0;
b) [ ] е;
c) [ ] 
;
d) [ ] 1;
12. Функция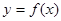 
имеет в точке производную, равную 1. Тангенс угла наклона касательной, проведенной к графику функции в этой точке, с положительным направлением оси Ох равен:
a) [ ] 3;
b) [ ] 2;
c) [ ] 0;
d) [ ] 1.
13. Какой из интегралов вычисляется методом замены переменной:
a) [ ] 
.
b) [ ] 
;
c) [ ] 
;
d) [ ]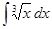 
.
14. Сходящаяся последовательность имеет:
a) [ ] 3 предела;
b) [ ] не имеет предела;
c) [ ] 2 предела;
d) [ ] 1 предел.
15. Если при переходе через критическую точку производная меняет знак с “+” на “–“, то есть:
a) [ ] точка максимума;
b) [ ] точка разрыва.
c) [ ] точка минимума;
d) [ ] точка перегиба.
16. Если числовой ряд 
сходится, то:
a) [ ] 
не существует.
b) [ ]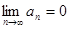 
;
c) [ ] 
;
d) [ ] 
.
17. Если смешанные производные 
и 
функции двух переменных непрерывны, то:
a) [ ] 
;
b) [ ] 
.
c) [ ] 
;
d) [ ] 
.
18. Какая из приведенных функций является функцией двух переменных:
a) [ ] 
;
b) [ ] 
;
c) [ ] 
.
d) [ ] 
.
19. Уравнение нормали к кривой 
в точке 
имеет вид:
a) [ ] 
;
b) [ ] 
;
c) [ ] 
.;
d) [ ] 
.
20. Если дифференцируемая функция имеет экстремум в точке , то:
a) [ ] 
;
b) [ ] 
;
c) [ ]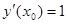 
;
d) [ ] 
.
21. Если в точке : , 
, то – точка:
a) [ ] разрыва.
b) [ ] минимума;
c) [ ] перегиба;
d) [ ] максимума.
22. Областью определения функции 
является промежуток:
a) [ ] 
;
b) [ ] 
;
c) [ ] 
;
d) [ ] 
.
23. Бесконечно большой последовательностью называется последовательность, имеющая предел, равный:
a) [ ] 1;
b) [ ] 1000;
c) [ ] 0;
d) [ ] 
.
24. Какое из приведенных уравнений не является дифференциальным уравнением:
a) [ ] 
.
b) [ ]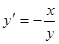 
;
c) [ ] 
;
d) [ ] 
.
25. Какое из приведенных уравнений является дифференциальным уравнением с разделяющимися переменными:
a) [ ] 
;
b) [ ] 
;
c) [ ]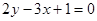 
.
d) [ ] 
.
Поиск по сайту: