Отделение корней. Универсальных приемов решения этой задачи пригодных для любых уравнений, не существует

Универсальных приемов решения этой задачи пригодных для любых уравнений, не существует.

Рассмотрим, известные из курса высшей математики графический и аналитический способы.

Графический метод.

Строится график функции f (х), а потом на оси отмечаются отрезки, локализующие абсциссы точек пересечения этого графика с осью О х.

Или более простой способ: сначала заменяется уравнение (1) равносильным ему уравнением

Затем строятся графики функций , в одной системе координат и на оси отмечаются отрезки, локализующие абсциссы точек пересечения этих графиков.

Аналитический способ. При решении задачи отделения корней используют следующие утверждения:

1 Если непрерывная на отрезке [ а;b ]функция f (x)принимает на его концах значения разных знаков (т.е. f (а) ·f (b) < 0), то уравнение (1) имеет на этом отрезке, по крайней мере, один корень.

2 Если функция f (x) к тому же ещё и монотонна, то корень на отрезке [ a; b ] единственный.

Пример 1. Провести отделение корней уравнения . Преобразуем заданное уравнение к равносильному уравнению 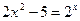и построим графики функций и в одной системе координат (рисунок 1).

Рисунок 1 – Графический способ

Из графика видно, что уравнение имеет три корня, расположенных на отрезках

[-1.8;-1.4], [2.1;2.2], [6;6,5].

Проверим аналитически существование корня на отрезке [-1.8; -1.4]. Функция на концах отрезка принимает значения разных знаков: , , что подтверждает существование корня.

Рассмотренные выше положения можно использовать для последовательного отделения всех корней уравнения (1). Пусть известно, что все интересующие нас корни находятся на отрезке [ А;В ], на котором функция f (x)определена и непрерывна. Тогда для отделения корней будем вычислять значения f (x), начиная с точки х = А, двигаясь вправо с некоторым шагом h до тех пор, пока не достигнем правого конца отрезка(рисунок 2). Если на концах частичного интервала [ x;x + h ] функция f (x), будет монотонной и будет иметь разные знаки, то отрезок [ x;x + h ] будем считать отрезком, содержащим корень.

Рисунок 2 – Отделение корней на всем отрезке

Заметим, что следует выбирать при отделении корней достаточно малые значения , чтобы избежать ситуаций, изображенных на рисунке 3.

Рисунок 3 – Случаи неправильного выбора шага

Поиск по сайту: