Метод простых итераций уточнения корней уравнения

Метод простых итераций (метод последовательных приближений) решения уравнения f (x)=0 состоит в замене исходного уравнения эквивалентным ему уравнением и построении последовательности , сходящейся при к точному решению. Чтобы последовательность сходилась необходимо выполнение достаточных условий сходимости.

Достаточные условия сходимости

Теорема. Пусть функция определена и дифференцируема на [ а, b ], причем все ее значения 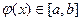. Тогда, если существует число q, такое, что на отрезке [ а, b ], то последовательность , k =0,1,2,..., сходится к единственному на [ а,b ] решению уравнения при любом начальном значении .

Замечание. Из условий теоремы следует, что метод итераций является самоисправляющимся, т.е. отдельная ошибка в вычислениях не влияет на конечный результат, так как ошибочное значение можно рассматривать как новое начальное значение х ₀.

Оценка погрешности приближений

Справедливы следующие оценки погрешности:

(2)

Отсюда ясно, что сходимость процесса итераций будет тем быстрее, чем меньше число q. Из формулы (2), следует:

.

В этом случае из неравенства

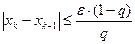
вытекает неравенство .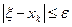

Выбор функции

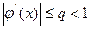Итак, остался открытым вопрос выбора функции в уравнении . Из теоремы следует, что следует подбирать функцию нужно так, чтобы . При этом нужно помнить, что скорость сходимости метода тем выше, чем меньше число q.

Существуют различные способы получения функции , например самый простой, но не самый эффективный, состоит в том, что из уравнения (1) каким либо образом выражают переменную x, тем самым получают уравнение вида .

Наиболее эффективным является следующий способ. Уравнение (1), преобразуют к виду

,

где - константа, которую можно вычислить исходя из условия ,следующим образом:

пусть на существует единственный корень уравнения (1) и - дифференцируема и производная сохраняет знак на , тогда:

если , то , а если , то , где .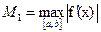

Тогда число q можно найти так:

.

Алгоритм метода

1 Вычислить коэффициент с и подставить его в функцию , вычислить

2 Вычислить и проверить достаточное условие сходимости 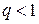, если оно выполняется, то перейти к п.3, иначе к п.6

3 Положить и к=0

4 Вычислить очередное приближение , положить к=к+1

5 Проверить условие завершения итераций , если оно выполняется, то принять за корень и завершить процесс, иначе положить и перейти к п.4

6 Конец

Пример. Уточнить методом простых итераций корень уравнения из предыдущего примера , с точностью на отрезке .

Решение. Заданное уравнение имеет вид (1), приведем его к виду , для этого:

1 Вычислим производную и проверим ее знак на отрезке :

.

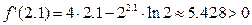
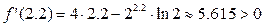В силу малости интервала делаем вывод, что функция на данном интервале возрастает, следовательно

2 Получаем итерационную формулу

3 Проверим на сходимость

(максимум достигается в точке ), следовательно метод сходится

4 Выберем начальное приближение, пусть это будет 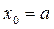и рассчитаем первое приближение

5 Проверим условие окончания итераций

Получили, что

6 Так как условие выполняется, то приближенное значение корня, найденное с точностью 0.01, все цифры верные.

Поиск по сайту: