Постановка задачи

Математическое моделирование и оптимальное управление 82

Вестник Нижегородского университета им. Н.И. Лобачевского, 2007, № 5, с. 82-86

УДК 62-80

СИНТЕЗ H_∞ - РЕГУЛЯТОРОВ ДЛЯ АКТИВНОГО ГАШЕНИЯ КОЛЕБАНИЙ ВЫСОТНЫХ СООРУЖЕНИЙ

О.П. Никонычев

Нижегородский госуниверситет им. Н.И. Лобачевского

oleg.nikonychev@gmail.com

В статье рассматривается задача стабилизации динамического объекта, заданного дифференциальными уравнениями для случаев измеряемого состояния и измеряемого выхода. Получена математическая модель стабилизирующей системы. Проведены численные эксперименты для регуляторов по состоянию и по выходу полного порядка. Сравниваются уровни гашения возмущений, достигаемые построенными регуляторами для десятиэтажного здания.

Введение

На протяжении трех последних десятилетий был разработан ряд систем управления, предназначенных для снижения рисков опасного воздействия со стороны окружающей среды, таких как землетрясения и сильные ветры, на городские инженерные сооружения. Многообразие рассматриваемых систем можно разделить на три группы: пассивные, активные, полуактивные и гибридные (сочетания предыдущих типов) [1, 2]. Данная статья посвящена построению активных систем управления на основе H_∞-регуляторов.

В статье рассматривается пример построения регуляторов по измеряемому состоянию и измеряемому выходу. Как показано в [3], минимальный уровень гашения возмущений обеспечивается регулятором по состоянию, однако, в реальных условиях данные о состоянии объекта могут отсутствовать, поэтому решается задача синтеза регуляторов по выходу. В качестве измеряемого выхода берется межэтажное смещение и смещение управляющих масс относительно этажей, к которым они прикрепляются. В предложенной в [3] реализации алгоритма синтеза H∞-регуляторов по выходу присутствует ранговое условие, вносящее нелинейность в систему линейных матричных неравенств. Чтобы избежать нелинейности, строится регулятор по выходу полного порядка, для которого ранговое условие выполняется всегда. Для решения задачи был применен аппарат линейных матричных неравенств, благодаря которому решение задачи значительно упрощается. Численные эксперименты произведены с использованием LMI Toolbox пакета MATLAB.

В разделе «Численные результаты» приводятся уровни гашения колебаний построенными регуляторами. Для десятиэтажного здания уровень гашения колебаний уменьшается более чем в 60 раз по сравнению с неуправляемым сооружением.

Постановка задачи

В качестве механической системы, моделирующей колебания высотного сооружения, будем рассматривать одномерную цепочку упругосвязанных материальных точек (этажей или секций сооружения), одна из которых (основание) совершает поступательное

Рис. 1. Схема трехэтажного здания с прикрепленными управляющими массами

движение, порождаемое сейсмическим воздействием. Предполагается, что масса основания намного превышает массы остальных материальных точек и поэтому влиянием движения секций сооружения на движение основания можно пренебречь [3]. Один из возможных вариантов технической реализации динамического гашения колебаний заключается в прикреплении к каждому этажу сооружения некоторой достаточно малой массы (по сравнению с общей массой сооружения), перемещаемой в соответствии с законом управления в форме обратной связи.

Будем рассматривать данную задачу как задачу синтеза -оптимального регулятора для управляемого объекта, описываемого системой дифференциальных уравнений

(1)

в которой 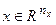– состояние, – возмущение, – управление, – управляемый выход, 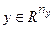– измеряемый выход. Синтез управления этим объектом состоит в построении регулятора, при котором уровень гашения возмущений в асимптотически-устойчивой замкнутой системе меньше заданного числа γ, т.е.

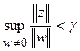. (2)

Такие регуляторы будем называть регуляторами с заданным γ. оптимальным регулятором будем называть регулятор с минимальным значением γ.

Для случая измеряемого состояния в объекте (1), когда 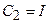и , управление выбирается в виде

. (3)

Уравнения замкнутой системы (1), (3) примут вид

(4)

где .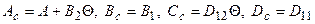

Список литературы

1. Fujino Y., Soong T.T., Spencer B. F. Jr. Structural Control: Basic Concepts and Applications // Proceedings of the ASCE Structures Congress. 1996. V. 4. P. 1277–1287.

2. Dyke S.J., Spencer B.F. Jr., Sain M.K, Carlson J.D. An Experimental Study of MR Dampers for Seismic Protection. // Smart Materials and Structures. 1998. V. 7. P. 693–703.

3. Баландин Д.В., Коган М.М. Синтез регуляторов на основе линейных матричных неравенств. М.: Физматлит, 2007.

Задание № 3. Конвертирование и перевод текста

Поиск по сайту: