 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Интернет-ресурсы. 1) http://www.youtube.com/watch?v=TxFmRLiSpKo (Геометрический смысл производной)
|
Читайте также: |
1) http://www.youtube.com/watch?v=TxFmRLiSpKo (Геометрический смысл производной)
2) http://www.youtube.com/watch?v=PbbyP8oEv-g (Лекция 1. Первообразная и неопределенный интеграл)
3) http://www.youtube.com/watch?v=2N-1jQ_T798&feature=channel (Лекция 5. Интегрирование по частям)
4) http://www.youtube.com/watch?v=3qGZQW36M8k&feature=channel (Лекция 2. Таблица основных интегралов)
5) http://www.youtube.com/watch?v=7lezxG4ATcA&feature=channel (Лекция 3. Непосредственное интегрирование)
6) http://www.youtube.com/watch?v=s-FDv3K1KHU&feature=channel (Лекция 4. Метод подстановки)
7) http://www.youtube.com/watch?v=dU_FMq_lss0&feature=channel (Лекция 12. Понятие определенного интеграла)
Задание № 1.
Даны вершины А (х1; у1), В (х2; у2), С (х3; у3) треугольника АВС. Требуется найти: А) уравнение стороны АС; Б) уравнение высоты, проведенной из вершины В; В) длину высоты, проведенной из вершины А; Г) величину угла В (в радианах); Д) уравнение биссектрисы угла В.
Варианты:
| 1. А(5; 3), В(-11; -9), С(-4; 15). | 6. А(-9; 6), В(3; 1), С(6; 5). |
| 2. А(-7; 2), В(5; -3), С(8; 1). | 7. А(20; 5), В(-4; 12), С(-8; 9). |
| 3. А(1; -15), В(6;-3), С(2; 0). | 8. А(-3; -7), В(2; 5), С(-2; 8). |
| 4. А(-8; 3), В(4; -2), С(7; 2). | 9. А(10; 1), В(-6; 13), С(1; -11). |
| 5. А(6; 3), В(-10; -9), С(-3; 15). | 10. А(0; -9), В(5; 3), С(1; 6). |
Задание № 2.
Найти матрицу С=3А-2В, где А=  , В (см. табл.1)
, В (см. табл.1)
Таблица 1 - Варианты задания 2.
1. 
| 2. 
| 3. 
| 4. 
| 5. 
|
6. 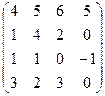
| 7. 
| 8. 
| 9. 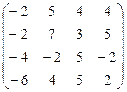
| 10. 
|
Задание № 3.
Вычислить определитель матрицы А (см. табл.2).
Таблица 2 - Варианты задания 3.
1. 
| 2. 
| 3. 
| 4.  
| 5. 
|
6. 
| 7. 
| 8. 
| 9. 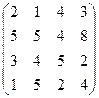
| 10. 
|
Задание № 4.
Дана матрица А (см. табл.3). Найти Матрицу А-1 и установить, что АА-1=Е.
Таблица 3 – Варианты задания 4.
1. 
| 2. 
| 3. 
| 4. 
| 5. 
|
6. 
| 7. 
| 8. 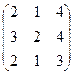
| 9. 
| 10. 
|
Задание № 5. Решить систему линейных алгебраических уравнений методом Крамера.
Варианты:
1. 
| 2. 
| 3. 
| 4. 
| 5. 
|
6. 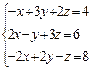
| 7. 
| 8. 
| 9. 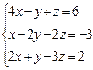
| 10. 
|
Задание № 6.
Решить 3 системы методом Гаусса (в табл. 5даны элементы расширенных матриц систем 4-х уравнений с 4-мя неизвестными).
Таблица 5 – Варианты задания 6.
| 1. |
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2. |
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3. |
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4. |
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5. |
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6. |
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7. |
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8. |
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9. |
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10. |
|
|
|
Задание № 7.
Z1, Z2 – комплексные числа. Выполнить действия:
А) Z1+ Z2; Б) Z1 × Z2; В) Z1/Z2.
Варианты:
| 1.Z1=5–4i; Z2=-1-i. | 2.Z1=-6+3i; Z2=2-i. | 3.Z1=3–2i; Z2=-45+i. | 4.Z1=4–3i; Z2=1-i. | 5.Z1=2–i; Z2=5-3i. |
| 6.Z1=3+2i; Z2=-3+4i. | 7.Z1=5–i; Z2=4-3i. | 8.Z1=6–2i; Z2=-1-4i. | 9.Z1=1–5i; Z2=-3+2i. | 10.Z1=5+2i; Z2=-3-2i. |
Задание № 8. Записать комплексное число в тригонометрической и показательной формах.
Варианты:
| 1.Z=-1-2i. | 2.Z=-1-i. | 3.Z=1+2i. | 4.Z=3+i. | 5.Z=2+i. |
| 6.Z=1-i. | 7.Z=2-i. | 8.Z=4-3i. | 9.Z=3-2i. | 10.Z=2+2i. |
Задание № 9. Вычислить указанные пределы, не используя правило Лопиталя.
Варианты:
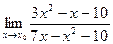
| А) X0 = 1 | Б) X0 = 2 | В) X0 = ¥ | |

| А) X0 = 3 | Б) X0 = -1 | В) X0 = ¥ | |

| А) X0 = 3 | Б) X0 = 1 | В) X0 = ¥ | |

| А) X0 = 2 | Б) X0 = 1 | В) X0 = ¥ | |

| А) X0 = -1 | Б) X0 = 1 | В) X0 = ¥ | |
 
| А) X0 = -2 | Б) X0 = 1 | В) X0 = ¥ | |

| А) X0 = 1 | Б) X0 = -1 | В) X0 = ¥ | |

| А) X0 = 2 | Б) X0 = 3 | В) X0 = ¥ | |

| А) X0 = 3 | Б) X0 = -3 | В) X0 = ¥ | |

| А) X0 = -3 | Б) X0 = -2 | В) X0 = ¥ |
Задание № 10. Найти производные функций.
Варианты:
| 1. | А)  ; В) ; В)  ; ;
| Б) 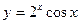 ; Г) ; Г) 
|
| 2. | А)  ; В) ; В)  ; ;
| Б)  ; Г) ; Г) 
|
| 3. | А)  ; В) ; В)  ; ;
| Б)  ; Г) ; Г) 
|
| 4. | А)  ; В) ; В)  ; ;
| Б)  ; Г) ; Г) 
|
| 5. | А)  ; В) ; В)  ; ;
| Б)  ; Г) ; Г) 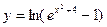
|
| 6. | А)  ; В) ; В)  ; ;
| Б)  ; Г) ; Г) 
|
| 7. | А)  ; В) ; В)  ; ;
| Б)  ; Г) ; Г) 
|
| 8. | А)  ; В) ; В)  ; ;
| Б)  ; Г) ; Г) 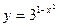
|
| 9. | А)  ; В) ; В)  ; ;
| Б)  ; Г) ; Г) 
|
| 10. | А)  ; В) ; В)  ; ;
| Б)  ; Г) ; Г) 
|
Задание № 11. И сследовать данную функцию методами дифференциального исчисления и построить ее график.
Варианты:
1. 
| 2. 
| 3. 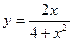
| 4. 
| 5. 
|
6. 
| 7. 
| 8. 
| 9. 
| 10. 
|
Задание № 12. Вычислить неопределенные интегралы.
Варианты:
| 1. | А)  ; ;
| Б)  ; ;
| В)  . .
|
| 2. | А)  ; ;
| Б)  ; ;
| В) 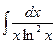 . .
|
| 3. | А)  ; ;
| Б) 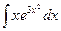 ; ;
| В)  . .
|
| 4. | А)  ; ;
| Б) 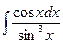 ; ;
| В)  . .
|
| 5. | А)  ; ;
| Б)  ; ;
| В)  . .
|
| 6. | А)  ; ;
| Б)  ; ;
| В)  . .
|
| 7. | А)  ; ;
| Б)  ; ;
| В) 
|
| 8. | А)  ; ;
| Б)  ; ;
| В) 
|
| 9. | А)  ; ;
| Б)  ; ;
| В)  . .
|
| 10. | А)  ; ;
| Б)  ; ;
| В)  . .
|
Задание № 13. Вычислить площадь фигуры, ограниченной линиями y=ax2+bx+c и y=mx+n (параметры a, b, c, m, n заданы в таблице). Построить график.
Варианты:
| a | b | c | m | n | |
| 1. | -4 | -1 | |||
| 2. | |||||
| 3. | |||||
| 4. | -6 | ||||
| 5. | -2 | -1 | |||
| 6. | |||||
| 7. | -6 | ||||
| 8. | |||||
| 9. | |||||
| 10. | -1 |
Задание № 14. В партии из N изделий n изделий имеют скрытый дефект (табл.6). Какова вероятность того, что из взятых наугад m изделий k изделий являются дефектными?
Таблица 6 – Варианты задания 13:
| N | n | m | k | |
| 1. | ||||
| 2. | ||||
| 3. | ||||
| 4. | ||||
| 5. | ||||
| 6. | ||||
| 7. | ||||
| 8. | ||||
| 9. | ||||
| 10. |
Задание № 15. Найти математическое ожидание, дисперсию и среднее квадратичное отклонение случайной величины Х, заданной законом распределения:
Варианты:
1.
| 2.
| ||||||||||||||||||||
3.
| 4.
| ||||||||||||||||||||
5.
| 6.
| ||||||||||||||||||||
7.
| 8.
| ||||||||||||||||||||
9.
| 10.
|
Желаю успехов!
Поиск по сайту: