 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Погрешности представления чисел
Представление числовой информации в персональном компьютере (ПК) как правило влечет за собой появление погрешностей, величина которых зависит от формы представления числа и от длины разрядной сетки ПК.
Абсолютная погрешность представления числа – это разность между истинным значением величины А и ее машинным представлением А*, то есть
(1)
Относительная погрешность представления числа – это отношение абсолютной погрешности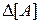 
к машинному представлению числа А*, то есть
(2)
Основным источником погрешности является ограниченная разрядная сетка ПК. При вычислениях часто возникает ситуация, когда полученный результат (его дробная часть) имеет больше разрядов, чем имеется в разрядной сетке. В этом случае приходится округлять (или отбрасывать) результат до нужного числа разрядов. Так, если разрядная сетка ПК имеет длину в n разрядов, то максимальное значение абсолютной погрешности будет равно 2-n, а минимальное значение равняется 0. Часто при оценке итоговой погрешности используют усредненную абсолютную погрешность 
, определяемую как
(3)
Абсолютное значение дробного числа в форме с фиксированной запятой находится в диапазоне
(4)
Относительная погрешность представления для максимального значения числа равняется
(5)
Обычно длина разрядной сетки 
, тогда 
и 
.
Относительная погрешность представления для минимального значения числа равняется
(6)
Видно, что погрешности представления малых чисел в форме с фиксированной запятой могут быть очень значительными, то есть соизмеримыми с самими числами.
Для числа в форме с плавающей запятой абсолютное значение нормализованной мантиссы находится в диапазоне
(7)
Для нахождения относительной погрешности представления числа в форме с плавающей запятой необходимо погрешность мантиссы умножить на величину порядка числа PA:
(8)
(9)
Видно, что относительная погрешность представления чисел в форме с плавающей запятой почти не зависит от величины числа. Поэтому все математические вычисления над дробными числами проводят, когда эти числа представлены в форме с плавающей запятой. Вычисления над целыми числами можно проводить, когда эти числа представлены в форме с фиксированной запятой. Но здесь следует контролировать, чтобы полученный результат не превысил пороговые значения, определяемые длиной разрядной сетки.
Поиск по сайту: