Логарифмическое дифференцирование

Дифференцирование функций, заданных неявно и параметрически. Логарифмическое дифференцирование.

Дифференцирование функций, заданных неявно.

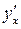Если функция задана уравнением , то для нахождения нужно продифференцировать обе части тождества 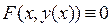по аргументу х и из полученного равенства найти 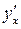как решение линейного уравнения.

Пример 1. Функция y (x) задана неявно уравнением . Найти .

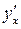Решение. Дифференцируем данное равенство по аргументу х, считая при этом, что y зависит от x:

.

Получилось равенство, линейное относительно 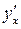, из которого находим 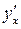как решение линейного уравнения

.

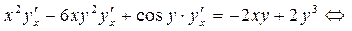
Ответ: .

Заметим,что производная неявно заданной функции выражается через аргумент х и функцию y (x).

Дифференцирование функций, заданных параметрически.

Пусть функция y (x) задана параметрически: , где x (t), y (t) – дифференцируемые функции параметра t.

Производная параметрически заданной функции находится по формуле .

Пример 2. Функция y (x) задана параметрически: Найти .

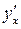Решение. Дифференцируем:

.

Производная параметрически заданной функции – также функция, заданная параметрически, поэтому ответ записываем в следующем виде: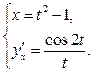

Пример 3. Составить уравнения касательной и нормали к кривой 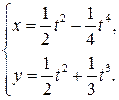в точке, соответствующей значению параметра .

----------------------------------------------------------------------------------------------------------------

Дифференцирование функций, заданных неявно и параметрически.

Логарифмическое дифференцирование. Стр. 1

Решение.

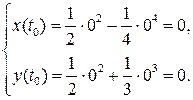
Уравнение касательной:

Уравнение нормали:

Логарифмическое дифференцирование.

Логарифмическое дифференцирование – это дифференцирование функции с предварительным ее логарифмированием. Оно используется для дифференцирования степенно-показательной функции , а также в случаях, когда y (x) упрощается при логарифмировании.

Пример 4. Найти производную функции .

Решение. Логарифмируем степенно-показательную функцию :

,

получим неявно заданную функцию y (x).

Применим правило дифференцирования неявно заданной функции:

.

Подставив , получим

.

Поиск по сайту: