Логарифмическое дифференцирование

Рассмотрим сложную функцию , где у=f(x). Запишем систему:

Выражение и называется логарифмической производной.

На практике очень часто приходится иметь дело с дифференцированием сложных степенных функций. Предварительное логарифмирование позволяет упростить эту задачу.

Пример: Таким образом,

Дифференциал функции

Вернемся к определению производной:

С помощью свойства связи предела и бесконечно малой величины (см. главу Пределы), запишем: или Так как - бесконечно малая и стремится к нулю, то вторым слагаемым можно пренебречь. Тогда первое слагаемое и называется дифференциалом функции у=f(х). Для того, чтобы подчеркнуть это определение, принято записывать Рассмотрим геометрический смысл дифференциала:

Дифференциалом функции у=f(х) первого порядка называется главная, линейная относительно приращения , часть приращения функции , равная произведению производной этой функции на приращение аргумента , обозначаемое в этом случае, как dx.

Эквивалентность записи докажем и по-другому: пусть у=х, тогда

Отсюда и следует Кроме того, определение дифференциала обосновывает представление производной, как отношения: из dy = следует

Свойства дифференциала аналогичны свойствам производной:

· dC = 0, C - постоянная (число).

· d(Cy)= Cdy.

· d(u 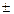v)= du 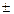dv.

· d(uv)= v du+u dv.

·

Приведем обозначения для дифференциалов высших порядков: и т.д.

Формула для дифференциала используется в приближенных вычислениях. Действительно, из следует: , откуда Чем меньше значение , тем точнее результат. К примеру, вычислим . Здесь Тогда или - практически точно.

Примеры решения задач

Приращение, скорость изменения, ускорение – важные характеристики функции, которые позволяют делать общие выводы об изменяемости и устойчивости исследуемых процессов и моделей. Рассмотрим ряд примеров, иллюстрирующих вычисление производных.

1. Найти приращение функции у = , если аргумент х изменяется от 1 до 1,4.

По определению

В нашем случае f (x) = 1² + 1 = 2; f (x +D x)=1,4²+1=2,96. Следовательно, D у = 2,96 – 2 = 1,96.

Ответ: 1,96.

2. у = х ² — 5 х + 4

Дифференцируем: .

3.

Предварительно перепишем это выражение: .

Теперь дифференцируем:

4.

Используем формулу производной от произведения. Имеем:

5. .

Используем формулу производной от дроби. Имеем:

6. у =(1+5 х)³.

Это - сложная функция. Преобразуем ее в систему.

, отсюда и

7. .

, отсюда и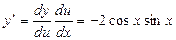

8.

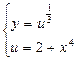, отсюда и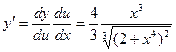

9.

, отсюда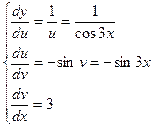

.

10.

.

11. 3 х + у ³ – 10 у ² + 6 = 0

Используем формулу для производной от неявной функции . Тогда

После простых преобразований имеем: .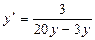

12.

Решение:

Учтем, что в правой части — произведение:

Тогда:

Отсюда после преобразований: .

13. Найти

Последовательно дифференцируя, получаем:

Следовательно, .

Ответ: 48.

14.

Функции такого типа дифференцируются с помощью логарифмической производной

Прологарифмируем заданное выражение: .

Тогда или

После подстановки выражения для у и упрощения окончательно получим

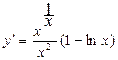или

15. С помощью дифференциала вычислить 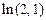, если известно, что .

Приближенная формула имеет вид В нашем случае х =2;

D х =0,1; . Следовательно,

.

Ответ: 0,743.

Вопросы для самоконтроля:

1. Приращение функции.

2. Производная функции – определение.

3. Геометрический и физический смыслы производной функции.

4. Табличные производные.

5. Теоремы о дифференцировании.

6. Производная сложной функции.

7. Производная неявной функции.

8. Производные высших порядков.

9. Логарифмическое дифференцирование.

10. Дифференциал функции.

11. Свойства дифференциала.

12. Приближенные вычисления с помощью дифференциала.

Поиск по сайту: