 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Непосредственное интегрирование (метод разложения)
С помощью свойств неопределенного интеграла и таблицы интегралов от элементарных функций становится возможным отыскание первообразных для несложных алгебраических выражений. Например,
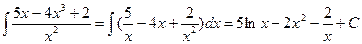
В большинстве случае для приведения к табличным интегралам необходимо выполнить предварительное преобразование подынтегрального выражения:
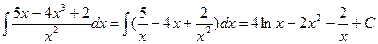
Метод замены переменной
Если подынтегральное выражение является достаточно сложным, то привести его к табличному виду часто удается одним из основных методов интегрирования - методом замены переменной (или методом подстановки). Основная идея метода состоит в том, что в выражение 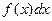 вместо переменной x вводится вспомогательная переменная u, связанная с х известной зависимостью
вместо переменной x вводится вспомогательная переменная u, связанная с х известной зависимостью 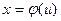 . Тогда подынтегральное выражение преобразуется к новому виду
. Тогда подынтегральное выражение преобразуется к новому виду 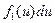 , т.е. имеем
, т.е. имеем
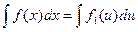
Здесь, по правилу дифференцирования сложной функции, 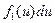 =
= 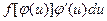 .
.
Если, после такого преобразования, интеграл 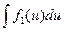 является табличным или значительно проще исходного, то замена переменной достигла своей цели.
является табличным или значительно проще исходного, то замена переменной достигла своей цели.
Пример:
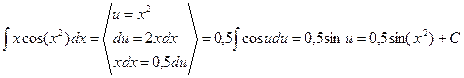
К сожалению, нельзя указать общих правил выбора «удачной» подстановки: такой выбор зависит от структуры конкретного подынтегрального выражения. В разделе 9.12 приводятся примеры, поясняющие различные способы выбора подстановки в ряде частных случаев.
Метод интегрирования по частям
Следующим основным общим методом является интегрирование по частям. Пусть u=u(х) и v=v(x) - дифференцируемые функции. Для произведения этих функций имеем, по свойству дифференциала:
d(uv) = v du + u dv или u dv = d(uv) - v du.
Интегрируя левую и правую части последнего равенства и учитывая свойство 3 неопределенного интеграла, получаем

Эта формула называется формулой интегрирования по частям для неопределенного интеграла. Для ее применения фиксируется разбиение подынтегрального выражения на два сомножителя и и dv. При переходе к правой части формулы первый из них дифференцируется (при нахождении дифференциала: du=u'dx), второй интегрируется: 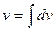 . Такой прием приводит к цели, если
. Такой прием приводит к цели, если 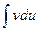 интегрируется легче, чем
интегрируется легче, чем 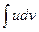 .
.
Пример: 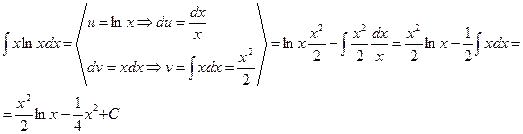
Иногда для получения результата формулу интегрирования по частям приходится применять несколько раз. Отметим, что при промежуточном вычислении 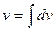 можно не дописывать произвольную постоянную C; легко убедиться, что в ходе решения она уничтожится.
можно не дописывать произвольную постоянную C; легко убедиться, что в ходе решения она уничтожится.
4. Интегрирование рациональных д робей
Если подынтегральная функция представляет собой алгебраическую дробь, то на практике достаточно часто встречаются два типовых случая:
· Степень числителя дроби больше или равна степени знаменателя (неправильная дробь). Для такой дроби можно разделить числитель на знаменатель известным из школьного курса методом деления углом (иначе – выделение целой части), после чего выполнить интегрирование. Пример:
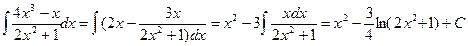
Здесь использовалась и замена переменной:
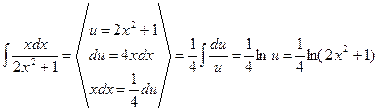
Для промежуточного расчет произвольную С можно не указывать, но в окончательном ответе она обязательна.
· Метод неопределенных коэффициентов. Если дробь – правильная и знаменатель разлагается на множители, то этот метод позволяет представить подынтегральную функцию суммой простых дробей, проинтегрировать которые уже несложно. Метод имеет большое значение не только в интегрировании. Покажем его суть на примере вычисления интеграла 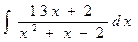 .
.
Разложив знаменатель дроби на множители, имеем: 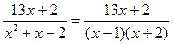 . Введем теперь предположение, что эту дробь можно представить суммой простых дробей:
. Введем теперь предположение, что эту дробь можно представить суммой простых дробей:
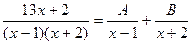
Здесь А и В – неизвестные коэффициенты, которые следует найти (неопределенные коэффициенты). Для этого приведем правую часть равенства к общему знаменателю:
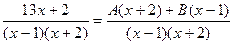
Сократив знаменатели и раскрыв скобки, получим
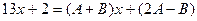
Теперь используем теорему: чтобы два алгебраических выражения были тождественно равны, необходимо и достаточно равенство их соответственных коэффициентов. Таким образом, получим систему из двух уравнений и решим ее:
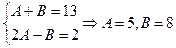
Следовательно,
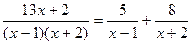 .
.
Возвращаясь к задаче интегрирования, получим
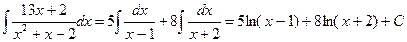
Поиск по сайту: