 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Скалярное произведение векторов
Скалярным произведением двух векторов 
и 
называется число = а1b1+a2b2+...+anbn. Часто вместо используется обозначение ( , ).
Скалярное произведение имеет следующие основные свойства:
· = - коммутативность.
· ( + 
)= + - дистрибутивность.
· k 
=(k ) = (k ) - любой из векторов можно умножить на число, не равное нулю.
· >0 при 
0; =0 только в случае =0 - скалярный квадрат не нулевого вектора всегда положителен.
· Если =0, то векторы и перпендикулярны (ортогональны).
Пространство всех векторов, в котором определено скалярное произведение, называется евклидовым пространством. Легко проверить, что орты описанных ранее пространств попарно ортогональны, т.к. 
=0 при i j. Таким образом, введенное евклидово пространство векторов имеет ортогональный ортонормированный базис.
Примеры решения задач
Рассмотрим примеры операций с векторами.
1. Для векторов 
, вычислить комбинацию 
Решение: 
.
2. Определить длину векторов 
и 
из предыдущего примера.
Так как длина вектора 
, то: для
для
3. Исследовать линейную зависимость 
и. 
Составим комбинацию l 1 + l 2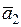 
= 0, т.е. 
. Переходя к алгебраической форме записи, имеем систему
откуда l 1 = l 2 = 0.
Таким образом, данные векторы линейно независимы.
4. Вектор 
разложить по базису; 
, 
.
Убедившись, что 
и 
линейно независимы (по образцу примера 3), запишем: 
, где k 1 и k 2 неизвестны, т.е. 
. В алгебраической форме имеем систему уравнений
, откуда 
Таким образом, искомое разложение: 
.
5. Найти скалярное произведение для векторов.
По определению скалярного произведения, имеем
.
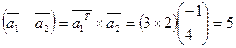6. Вычислить скалярный квадрат вектора.
Решение:.
Вопросы для самоконтроля:
1. Определение вектора в n –мерном пространстве.
2. Длина вектора.
3. Линейная комбинация векторов.
4. Линейная зависимость векторов.
5. Разложение вектора по базису.
6. Орты.
7. Разложение вектора по ортам.
8. Скалярное произведение векторов и его свойства.
Поиск по сайту: