Выражение координат произвольного вектора через компоненты радиус-векторов

!!!!!!!!!!!!!!!не нашла

Направляющие косинусы вектора и их свойства. Направляющие косинусы вектора a – это косинусы углов, которые вектор образует с положительными полуосями координат. Чтобы найти направляющие косинусы вектора a необходимо соответствующие координаты вектора поделить на модуль вектора._св-во: cos2 α + cos2 β = 1

Длина отрезка. Рассчитаем длину отрезка А, для этого найдем квадратный корень:

A = √(X²+Y²) = √ ((X2-X1)²+(Y2-Y1)²).

Скалярное произведение векторов и его свойства. Геометрическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними:

a · b = |a| · |b| cos α

Алгебраическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.

Св-ва:1) Операция скалярного умножения коммуникативна:

a · b = b · a

2) Операция скалярного умножения дистрибутивна:

(a + b) · c = a · c + b · c

3) Скалярное произведение вектора самого на себя равно квадрату его модуля:

a · a = |a|2

4) Если скалярное произведение двух не нулевых векторов равно нулю, то эти вектора ортогональны:

a ≠ 0, b ≠ 0, a · b = 0 <=> a ┴ b

Выражение скалярного произведения векторов через их координаты. Пусть заданы два вектора скалярно умножим: т.е. Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.

Угол между векторами. Определение угла φ между ненулевыми векторами а = (ax; ay; az) и b=(bх; bу; bz):

Отсюда следует условие перпендикулярности ненулевых векторов а и b

Деление отрезка в заданном отношении. Это в тетради расписано как задача!!!!!!!

Геометрический смысл скалярного произведения векторов.

Векторное произведение векторов и его свойства. Векторным произведением вектора а на вектор b называется вектор с, который:

1. Перпендикулярен векторам a и b, т. е. с^а и с^b;

2. Имеет длину, численно равную площади параллелограмма, построенного на векторах а и b как на сторонах (см. рис. 17), т. е.

3.Векторы a, b и с образуют правую тройку.

4/ его длина равна произведению длин векторов и на синус угла между ними

Св-ва: антикоммутативность

свойство дистрибутивности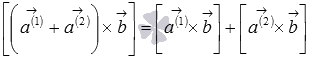

сочетательное свойство или

Выражение вектора векторного произведения векторов через координаты. В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов и есть вектор , где - координатные векторы.

Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты , во второй строке находятся координаты вектора а в третьей – координаты вектора в заданной прямоугольной системе координат: если разложить,то получим_

Геометрический смысл модуля векторного произведения векторов. длина векторного произведения векторов и равна площади параллелограмма со сторонами и и углом между ними, равным .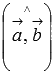

Смешанное произведение векторов и его свойства. Здесь первые два вектора перемножаются векторно, а их результат скалярно на третий вектор. Такое произведение называется векторноскалярным, или смешанным, произведением трех векторов. Смешанное произведение представляет собой некоторое число.

Св-ва: 1. Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е. (а х b)•с=(b х с)•а=(с х а)•b.2) Смешанное произведение не меняется при перемене местами знаков вкторного и скалярного умножения, т. е. (ахb)•с=а*(bx с).3) Смешанное произведение ненулевых векторов а, b и с равно нулю огда и только тогда, когда они компланарны

Геометрическое истолкование смешанного произведения векторов. геометрический смысл выражения (ахb)*с. Построим параллелепипед, ребрами которого являются векторы а, b, с и вектор d =ахb смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку.

Поиск по сайту: