Матричные уравнения

Любая система линейных уравнений может быть легко переписана в матричной форме:
или А = .

Умножим полученное матричное уравнение на матрицу А слева: А А = А , откуда = А , т.е. при известной матрице А можно получить решение для произвольных значений b 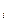в векторе . Относительно привычного нам вектора отметим, что можно решать и самые общие уравнения, в которых неизвестными являются уже не векторы, а матрицы, причем не всегда квадратные: АХ=В Х= А В; ХА=В Х= В А - здесь для получения ответа надо умножить уравнение на А справа.

Степень и функции матриц

Для квадратных матриц целая степень матрицы определяется так же, как и для обычных чисел: А =А А А ... А (n сомножителей). При этом полагается: А =Е; А =А.

В целом ряде случаев необходимо использовать отрицательную степень матрицы. Она может быть введена по правилу: А = (А ) .

С помощью этих формул можно решать задачи типа: если известен закон изменения f(x), то: определить f (A) - функцию от матрицы. Например, если f(x)= 2x -3x+5, то f (A)= 2 A -3 A +5 E. Если f(x)= 4 x + , то f (A)=4 A +(A - 2 E) .

Ясно, что матрица А должна быть такой, чтобы все операции имели смысл. Единичная матрица Е использована для формального преобразования обычных чисел к матричной записи. По размерности она должна соответствовать матрице А.

Примеры решения задач

Свободное владение алгеброй матриц является предварительным условием для изучения методов профессиональной обработки дискретных моделей. Рассмотрим ряд примеров по операциям с матрицами.

1.Вычислить линейную комбинацию 3 А +2 В, если A= ; B= .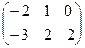

Решение:

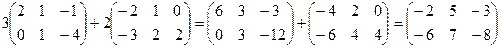
2.Примеры на вычисление произведений:

;

.

Эти примеры полностью иллюстрируют учет размерности сомножителей в произведениях матриц. В дальнейшем размерности не приводятся.

3. Примеры на учет свойств транспонирования.

Пусть, , . Тогда

, ,.

.

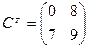
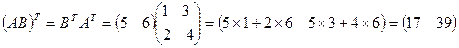
В последних двух произведениях обратим внимание на обязательную симметричностьрезультата.

4. Обратить матрицу

Приведем все вычисления по пунктам:

· следовательно, заданная матрица имеет обратную .

· Вычисляем адъюнкты: А ₁₁=7; А ₂₁= –8; А ₁₂= –3; А ₂₂=2.

· Союзная матрица

· Обратная матрица:

· Проверка: – верно.

5. Обратить матрицу

· . Матрица – вырожденная, обратной не имеет.

6. Обратить матрицу

·

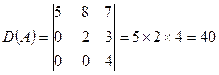
Матрица имеет обратную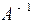

· Адъюнкты:

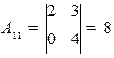· ; А ₂₁= – = –32; А ₃₁ = =10;

· А ₁₂= – =0; А ₂₂ = =20; А ₃₂ = – = –15;

· А ₁₃ = =0; А ₂₃ = – =0; А ₃₃ = =10.

·. Союзная матрица:.

· Обратная матрица:

· Проверка:

– верно

Поиск по сайту: